一、北京理工复试流程复试考察形式(笔试+面试)
北京理工大学机械类专业复试流程如下:
此次机车0102方向复试在27号一天内完成,29号下午便会公布成绩。鉴于时间紧凑,仅一天时间,即便某一场发挥欠佳,也别让其影响后续场次,保持良好心态至关重要。
复试面试涵盖五个部分:英语口语占10分,专业知识面试30分,综合面试30分,专业课笔试20分,英语听力10分。
其中,专业知识面试与综合面试在时间安排上紧密相连、依次开展。
英语口语环节,由两位老师负责,一位负责记录,一位提问,问题包含自我介绍、家乡及学校介绍等内容。
专业知识面试时,考生先做简短版自我介绍,老师会询问本科所学课程,若涉及熟悉课程,还会就课程知识深入提问,约有五位老师,每位老师提1 - 2个问题。
综合面试要求做完整版本自我介绍,接着围绕毕业设计以及车辆相关问题提问,若未学过车辆专业知识,会让考生基于自身理解去思考作答。
专业课笔试需在机械原理和机械设计、汽车理论中二选一,我选的是机械原理和机械设计,题型有填空、选择、简答、计算这几类。
英语听力共10题,每题1分,前5题类似四六级的对话选题,后5题类似七选五形式,从七个选项里挑出五个对应答案。
复试推荐参考教材: 1. 《机械设计》(第3版),北京理工大学出版社,孔凌嘉、王晓力主编(或者濮良贵老师主编的、高等教育出版社出版的《机械设计》);2. 《机械原理》,北京理工大学出版社,丁洪生、荣辉主编(或者孙恒老师主编的《机械原理》)。
二、北理复试面试真题
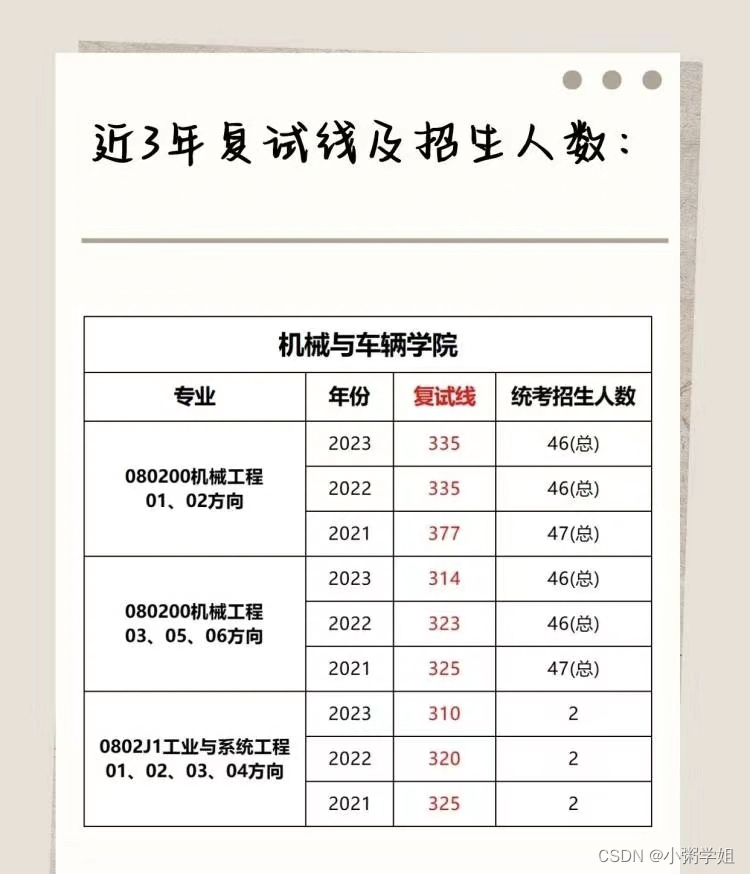
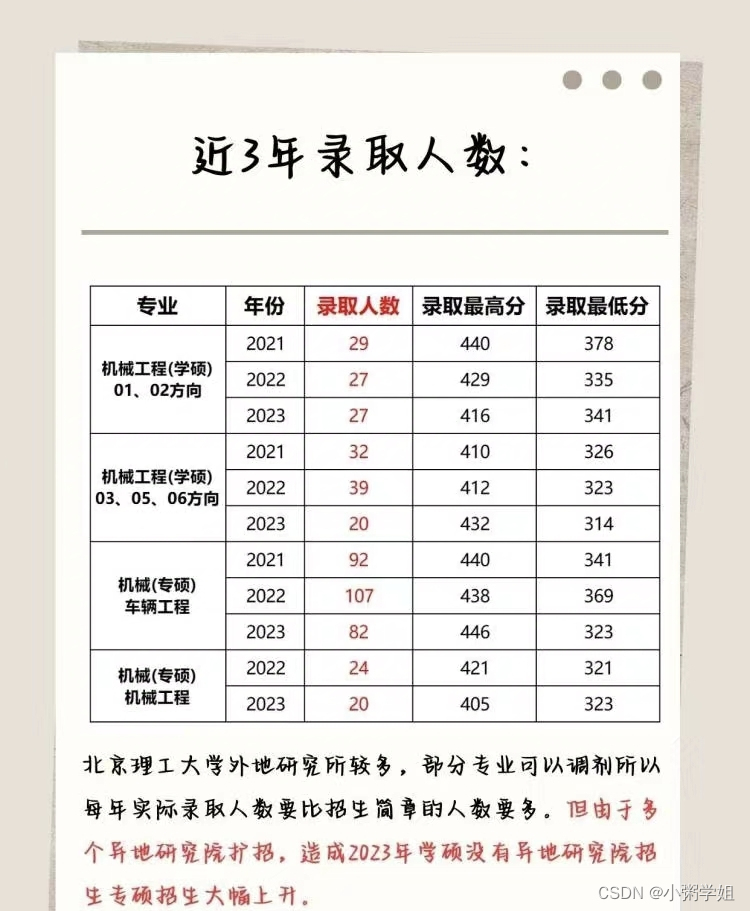
三、复试线及录取分数要求