来源:[Mac 开启 ssh 登陆 | HeyFE](https://blog.heyfe.org/blog/mac-ssh-server.html)
家里一台 Mac mini,一台 MacBook Air,平时比较习惯用 MacBook,但是偶尔需要上 mini 上去修改一些服务,每次都要切换键盘鼠标什么的比较麻烦,所以干脆把 Mac mini 的 ssh server 打开了。
开启
首先在从 General 中进入到 Sharing 配置:
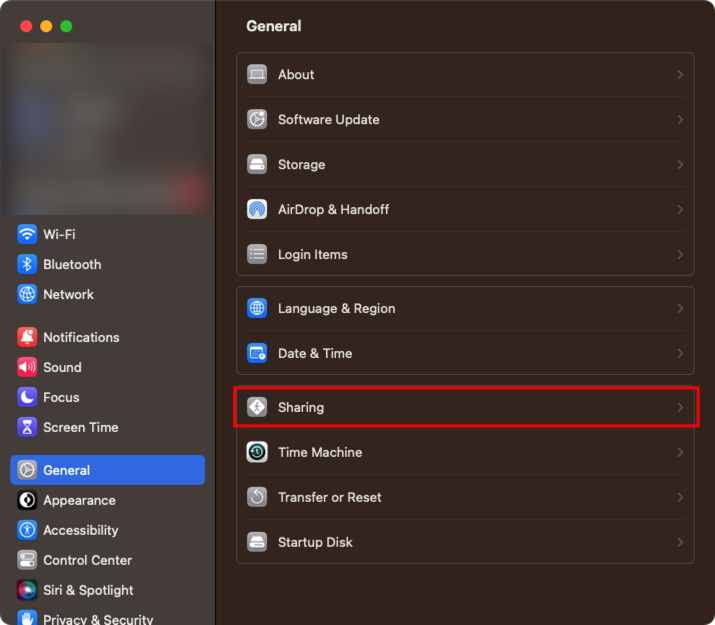
然后开启 Remote Login 即可:
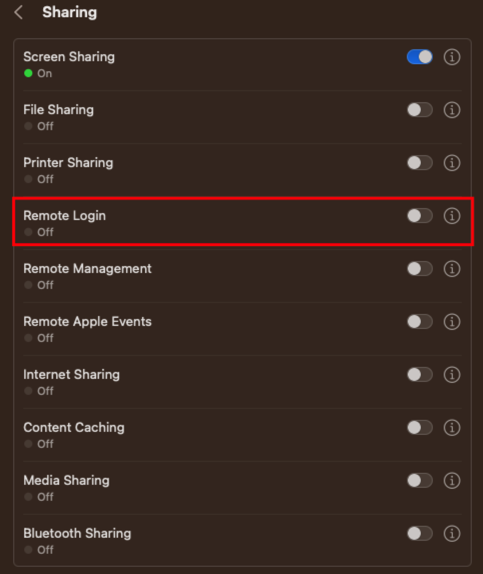
如果磁盘访问权限不够可以开启全盘访问权限再试:
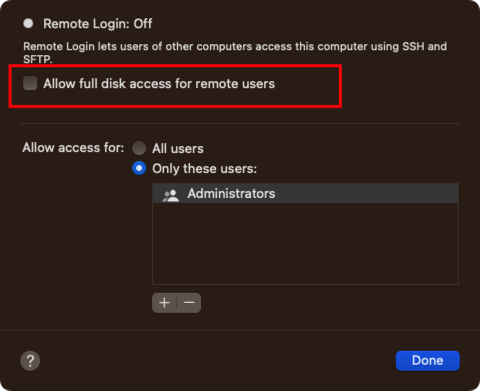
注意开启后 SFTP 服务也会一并生效。
连接
然后就可以从另一台电脑中通过局域网 ssh 到这台 Mac 了:

如果忘记自己的 Mac 用户 ID,可以直接打开 terminal 然后使用 pwd 查看主路径,一般主路径文件夹名称就是自己的用户 ID。
开启后可以创建 authorized_keys 然后将自己的 ssh public key 丢进去,这样就不用输入密码了:
touch ~/.ssh/authorized_keys
chmod 600 ~/.ssh/authorized_keys
echo {public_key} >> ~/.ssh/authorized_keys也可以顺便在 .ssh/config 添加上。然后就可以使用 VSCode SSH Remote 上去开发了。
Mac下ssh root@localhost多次输入密码 提示:permission denied解决方案
、问题描述
在做渗透测试时,需要测试自己写的脚本是否可以正常运行,所以使用本机ip地址来做验证,但是发现ssh root@localhost,会提示没权限。
二、终极解决方案
在网上看到很多解决方案,试了好多也没啥用,最终还是通过下面的方法解决的。
1、在命令行输入如下命令:
| 1 |
sudo vim /etc/ssh/sshd_config
|
2、修改PermiRootLogin 为yes,如下图
