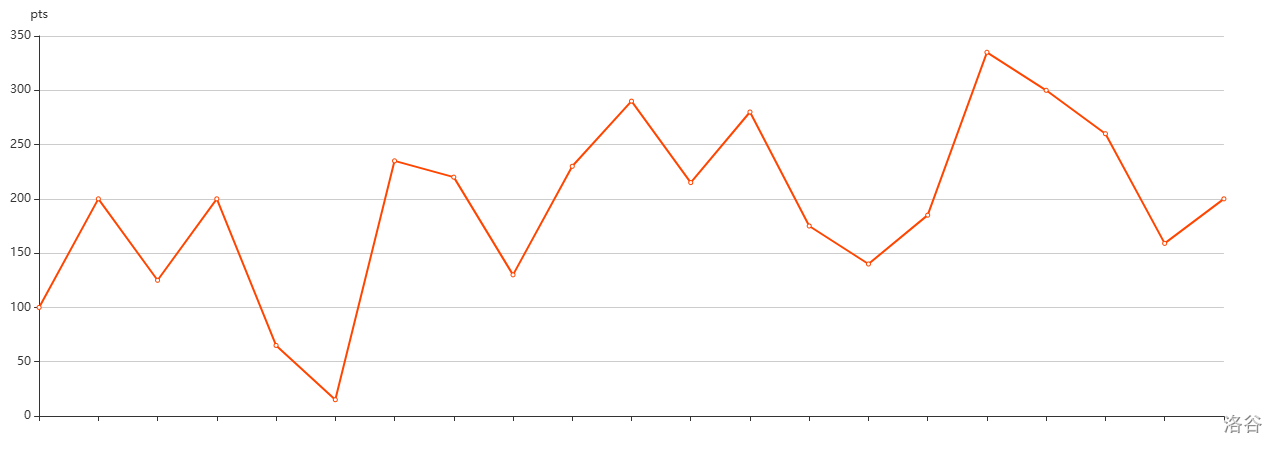
| 日期 | 类型 | A | B | C | D | 总分 | 小经验 |
|---|---|---|---|---|---|---|---|
| 0820 | 省选/互测赛 | \(\color{green}{数论分块/性质}\) | \(\color{blue}{期望}\) | \(\color{blue}{生成函数/多项式}\) | 16 | 大样例/long long | |
| 0824 | 省选/互测赛 | \(\color{green}{FWT}\) | \(\color{green}{Ad-hoc}\) | \(\color{blue}{数据结构优化DP}\) | 200 | 打暴力 | |
| 0827 | NOIP/数论专场 | \(\color{blue}{暴力}\) | \(\color{blue}{同余}\) | \(\color{blue}{斐波那契}\) | \(\color{blue}{长剖优化计数}\) | 9 | 检查,不要死磕一道题 |
| 0829 | 省选/互测赛 | \(\color{green}{随机化}\) | \(\color{blue}{虚树/阅读理解}\) | \(\color{red}{多项式/推式子}\) | 140 | 好好看每一道题 | |
| 0830 | 省选/互测赛 | \(\color{blue}{暴力}\) | \(\color{green}{数据结构}\) | \(\color{green}{期望/组合数学}\) | 200 | 好好检查,算好上界 | |
| 0903 | NOIP/计数专场 | \(\color{green}{容斥}\) | \(\color{blue}{容斥/前缀和优化}\) | \(\color{blue}{圆方树/树形\ DP}\) | \(\color{blue}{行列式/优化/组合计数}\) | 100 | 好好打暴力,不要破釜沉舟 |
| 0905 | 省选/雅礼 | \(\color{green}{线段树}\) | \(\color{blue}{折半/二分图}\) | \(\color{green}{李超优化\ DP}\) | 245 | 代码调快点,不要慌 | |
| 0908 | CSP-S | \(\color{green}{同余}\) | \(\color{blue}{异或贪心/Trie}\) | \(\color{blue}{搜索}\) | \(\color{blue}{数据结构}\) | 100 | 好好看一个题,思路打开 |
| 0909 | CSP-S | \(\color{green}{Trie}\) | \(\color{blue}{折半}\) | \(\color{blue}{数据结构优化期望\ DP}\) | \(\color{blue}{数学神题}\) | 200 | 打好暴力 |
| 0911 | NOIP | \(\color{green}{}构造\) | \(\color{blue}{性质}\) | \(\color{blue}{数据结构}\) | \(\color{blue}{杂题}\) | 125 | 用好cerr,记得最后 5min 检查 |
| 0915 | CSP-S | \(\color{green}{单调栈}\) | \(\color{blue}{k\ 路归并}\) | \(\color{blue}{神奇\ DP}\) | \(\color{green}{原题}\) | 200 | 不要看榜,争取做到最好 |
| 0916 | CSP-S | \(\color{blue}{DP}\) | \(\color{blue}{四边形不等式}\) | \(\color{blue}{模拟}\) | \(\color{blue}{圆方树}\) | 65 | 开拓思维,把每道题都看看,想到就先写 |
| 0922 | CSP-S | \(\color{blue}{最短路}\) | \(\color{blue}{排序构造}\) | \(\color{blue}{期望\ DP}\) | \(\color{blue}{mst\ 神秘题}\) | 15 | 打对拍,排序题先想归并 |
| 0928 | CPS-S | \(\color{green}{换根\ DP}\) | \(\color{green}{k\ 路归并}\) | \(\color{blue}{数学\ DP}\) | \(\color{blue}{简单博弈}\) | 235 | 想题想快一点 |
| 1002 | CSP-S | \(\color{green}{状压\ DP}\) | \(\color{blue}{找规律}\) | \(\color{blue}{贪心\ mst}\) | \(\color{green}{毛毛虫剖分}\) | 220 | 操作类题多手玩 |
| 1003 | CSP-S | \(\color{green}{简单\ DP}\) | \(\color{blue}{根号分治}\) | \(\color{blue}{大模拟}\) | \(\color{blue}{搜索}\) | 130 | 每道题都想一下 |
| 1004 | CSP-S | \(\color{blue}{签到题}\) | \(\color{blue}{性质题}\) | \(\color{green}{简单题}\) | \(\color{blue}{巧妙树数题}\) | 230 | 不要相信大样例 |
| 1005 | CSP-S | \(\color{green}{小模拟}\) | \(\color{green}{小构造}\) | \(\color{blue}{数数题}\) | \(\color{blue}{抽象优化题}\) | 290 | 注意积累思路 |
| 1006 | CSP-S | \(\color{green}{最小生成树}\) | \(\color{blue}{meet-in-middle}\) | \(\color{blue}{妙妙题}\) | \(\color{blue}{线段树优化\ DP}\) | 215 | 注意常数优化 |
| 1008 | CSP-S | \(\color{green}{找规律}\) | \(\color{green}{kmp}\) | \(\color{blue}{期望\ DP 题}\) | \(\color{blue}{线段树优化建图}\) | 280 | 最后一个小时再打暴力 |
| 1010 | CSP-S | \(\color{green}{简单\ DP}\) | \(\color{blue}{矩阵加速\ DP}\) | \(\color{blue}{期望数学题}\) | \(\color{blue}{构造}\) | 175 | 去构造几组小样例卡自己猜的性质 |
| 1012 | CSP-S | \(\color{green}{简单\ DP}\) | \(\color{blue}{数位\ DP}\) | \(\color{blue}{建图+线段树}\) | \(\color{blue}{2-sat}\) | 140 | 认真检查 |
| 1013 | CSP-S | \(\color{green}{二分}\) | \(\color{blue}{贪心}\) | \(\color{blue}{前缀和}\) | \(\color{blue}{性质+数据结构优化\ DP}\) | 185 | 认真检查 |
| 1015 | CSP-S | \(\color{green}{树上背包}\) | \(\color{green}{二分图构造}\) | \(\color{green}{状压\ DP}\) | \(\color{blue}{根号分治}\) | 335 | 不知道 |
| 1017 | CSP-S | \(\color{green}{性质题}\) | \(\color{green}{贪心}\) | \(\color{green}{线段树}\) | \(\color{blue}{思维}\) | 300 | 打有保证的暴力 |
| 1019 | CSP-S | \(\color{green}{简单题}\) | \(\color{green}{乱贪}\) | \(\color{blue}{根号分治}\) | \(\color{blue}{李超优化\ DP}\) | 260 | 认真看数据范围 |
| 1020 | CSP-S | \(\color{blue}{简单题}\) | \(\color{green}{暴力}\) | \(\color{blue}{2\ 合\ 1\ 性质题}\) | \(\color{blue}{根号分治容斥}\) | 159 | 不要看错题了 |
| 1023 | CSP-S | \(\color{green}{简单题}\) | \(\color{green}{树上小操作}\) | \(\color{blue}{构造}\) | \(\color{blue}{状压}\) | 200 | 为什么不会 t4 |
| 1029 | NOIP | \(\color{green}{构造}\) | \(\color{blue}{二分贪心}\) | \(\color{blue}{二分图+线段树优化}\) | \(\color{blue}{最短路}\) | 118 | 记得测自造大样例 |
搞笑:
0820
B
我们首先把起点视为一个 \(p=0\) 的传送点,那么考虑 一个传送点 \(i\),它的结局就两种:直接走到终点和被传送。
我们设 \(P=\sum\limits_{i=1}\limits^{k}p_i\),为了方便。
我们首先考虑直接走到终点的概率,不妨设 \(s_i=\sum\limits_{j=1}\limits^{n}d_j-a_{i,j}\) 表示从 \(i\) 到终点的步数,那么直接走到终点的概率 \(q_i=\frac{(1-P)^{s_i}}{n^s}\times \frac{s_i!}{\prod\limits_{j=1}\limits^{n}(d_j-a_{i,j})!}\),特别地,当存在 \(a_{i,j}>d_j\) 时,\(q_i=0\)。我们考虑它的组合意义,前面一部分就是不传送的概率和每一步都按照规划走的概率,后一部分就是走到终点的方案数,就是一个可重集排列。
设 \(f_i\) 表示从 \(i\) 出发到终点的期望步数,我们考虑传送之后的期望步数对于所有传送点都是相等的,我们设它是 \(g=\sum\limits_{i=1}\limits^{k}\frac{p_i}{P}f_i\)。
所以我们可以得出 \(f_i=q_is_i+\frac{1}{P}-q_i(\frac{1}{P}+s_i)\)。考虑后面那一部分的意义,首先如果我们没有终点那么期望显然就是 \(\frac{1}{P}\),但是由于我们有终点,所以我们需要减去走到终点的贡献就是 \(q_i(\frac{1}{P}+s_i)\),因为走到终点是既定事实,所以我们到了终点之后还会花 \(\frac{1}{P}\) 步,所以步数就是 \(\frac{1}{P}+s_i\)。在这个式子里面只有 \(f_i\) 和 \(g\) 是一开始算不出来的,所以我们等价于得到了一个 \(f_i\) 和 \(g\) 的关系式,用 \(g\) 表示 \(f_i\) 之后代入到 \(g\) 的定义式就能得到关于 \(g\) 的方程,就能把 \(g\) 算出来了,那么答案就是 \(f_0\)。
0829
B
C
我们观察这个式子,发现后面那个乘积式很像二项式定理,所以我们按照那个方法展开它:
\[\sum\limits_{j=1}\limits^{n}a_j\sum\limits_{k=0}\limits^{i}b_j^kc(i,i-k) \]其中 \(c(i,i-k)\) 表示从 \(c_{1,i}\) 中选出 \(i-k\) 个 \(c\) 的乘积的和,本质上是 \([x^{i-k}]\prod\limits_{j=1}\limits^{i}(1+c_ix)\)(组合意义可得),我们设多项式 \(C_{[l,r]}=\prod\limits_{i=l}\limits^{r}(1+c_ix)\),那么 \(c(i,i-k)=[x^{i-k}]C_{1,i}\)。
我们把 \(c(i,i-k)\) 代换得到:
\[\sum\limits_{j=1}\limits^{n}a_j\sum\limits_{k=0}\limits^{i}b_j^k[x^{i-k}]C_{[1,i]} \]交换求和顺序:
\[\sum\limits_{k=0}\limits^{i}[x^{i-k}]C_{[1,i]}\sum\limits_{j=1}\limits^{n}a_jb_j^{k} \]我们发现 \(b_j^k\) 的 \(k\) 在指数上,非常不好,所以我们用生成函数把它变成多项式的系数:\(b_j^k=[x^k]\frac{1}{1-b_jx}\),我们代入:
\[\sum\limits_{k=0}\limits^{i}[x^{i-k}]C_{[1,i]}\sum\limits_{j=1}\limits^{n}a_j[x^k]\frac{1}{1-b_jx} \]我们干脆把 \(a_j\) 也当成系数放到 \(b\) 的多项式里面,设多项式 \(S=\sum\limits_{j=1}\limits^{n}a_j\frac{1}{1-b_jx}\),那么原式:
\[\sum\limits_{k=0}\limits^{i}[x^{i-k}]C_{[1,i]}[x^k]S \]这描述的其实就是 \([x^i]C_{[1,i]}S\)。
我们先来考虑 \(S\) 怎么算,考虑我们如果直接算的话多项式求逆需要保留 \(n\) 项,计算复杂度为 \(O(n^2\log n)\),所以我们通分它:\(S=\frac{\sum\limits_{j=1}\limits^{n}a_j\prod\limits_{k=1}\limits^{n}[j\neq k](1-b_kx)}{\prod\limits_{j=1}\limits^{n}(1-b_jx)}\)。这个东西可以分治 ntt 做。
0903
[20240903] 串计数
考虑我们可以计算一个条件都不满足的,再用 \(2^n\) 减去得到答案。
我们首先考虑每一个下标的贡献只和 \(0/1\) 的数量有关,所以我们可以把串 \(1\) 改为全 \(1\) 串,如果这个位置原来是 \(0\),那么就把三个串的对应位置全部异或 \(1\) 即可。
那么我们考虑现在每个位置只有 \(4\) 种:\(100,111,101,110\),我们假设它们的数量分别为 \(x_1,x_2,x_3,x_4(x_1+x_2+x_3+x_4=n)\)。
我们假设在这 \(4\) 种中最终的串有 \(y_1,y_2,y_3,y_4\) 个位置是 \(1\),那么 \(dis(s_1)=x_1-y_1+x_2-y_2+x_3-y_3+x_4-y_4>r_1,dis(s_2)=y_1+x_2-y_2+y_3+x_4-y_4>r_2,dis(s_3)=y_1+x_2-y_2+x_3-y_3+y_4>r_3\),稍微化简得到 \(y_1+y_2<x_1+x_2+x_3+x_4-y_3-y_4-r_1,y_1-y_2>r_2-x_2-y_3-x_4+y_4,y_1-y_2>r_3-x_2-x_3+y_3-y_4\),不难发现我们等价于是在统计一个矩形的答案。
考虑由于一种 \(y_1,y_2,y_3,y_4\) 的贡献是 \(C_{x_1}^{y_1}C_{x_2}^{y_2}C_{x_3}^{y_3}C_{x_4}^{y_4}\),我们可以先把上面只与 \(y_1,y_2\) 有关的矩形内点的权算出来,这里的复杂度为 \(O(n^2)\),我们可以做一个前缀和,再 \(O(n^2)\) 枚举 \(y_3,y_4\),这样就可以做到总复杂度为 \(O(n^2)\) 了。
[20240903] 图计数
我们首先考虑
0908
异或匹配
从高到低位考虑,假如当前考虑第 \(d\),位,如果 \(d\) 位为 \(1\) 的数个数为偶数,那么可以分治处理,答案就是为 \(0\) 的和为 \(1\) 的取 \(\max\);如果是奇数个,说明最后答案的 \(d\) 位一定为 \(1\),等价于从 \(d\) 位为 \(0\) 的和 \(d\) 位为 \(1\) 的选取两个异或最小,用 Trie 优化,复杂度为 \(O(n\log n)\)。
矩阵游戏
考虑如果我们知道第 \(i-1\) 行的颜色,我们就能够推出第 \(i\) 行的颜色,那么我们直接枚举第 \(1\) 行颜色,暴力搜索,复杂度是 \(O(3^nn^2)\)。
选择首都
假设点 \(u\) 的答案为 \(ans_u\),那么和 \(u\) 直接相连的任意点 \(v\) 都一定有 \(|ans_u-ans_v|\le 1\)。我们可以先一个 \(\log\) 去二分点 \(1\) 的答案,再遍历一边树,那么假设判断点 \(u\) 是否能做到距离不超过 \(k\) 的复杂度是 \(O(T)\),则总复杂度为 \(O(T\log n+nT)\)。
考虑我们可以做到 \(O(n)\) 判定,具体来说,如果点 \(u\) 子树内距离它最深的点的距离大于 \(k-1\) 了,我们就必须从根向 \(u\) 连一条边,所以直接 dfs 整棵树即可。
考虑我们优化这个过程,具体来说,每次找出距离当前点最远的点,跳 \(k-1\) 级祖先,把它的祖先的子树的所有点都删掉,如果这样做 \(k\) 次之后最远点距离不超过 \(k\) 那么就可行,这个东西可以用线段树维护,跳 \(k\) 级祖先用倍增,复杂度为 \(O(k\log n)\),所以总复杂度为 \(O(n\log n+nk\log n)\)。
0909
顺序对
折半,卡常。
随机游走
我们如果能把一个点的期望 \(f_u\) 全部用它的祖先表示,那么这个题就可做了。考虑叶子显然能做到这个事情。对于点 \(u\),\(f_u=1+\frac{\sum\limits_{v\in e_u}f_v}{|e_u|}\),如果所有 \(f_v\) 都只和祖先有关,那么我们可以把所有和 \(u\) 有关的项移到左边,化简它,这样我们就能把 \(u\) 用它的祖先表示出来了。对于新加的返祖边,由于它本来就是祖先,我们保留即可。用线段树合并维护这个过程,复杂度为 \(O((n+m)\log n)\)。
数论函数
我们考虑这个问题可以转化为求 \(\sum\limits_{k\ge 1}\sum\limits_{i=1}\limits^{ma}\sum\limits_{j=1}\limits^{mb}[f(a,b)\ge k]\)。
我们现在给出一个性质:\(b+i|a+wi^2\) 等价于 \(b+i|a+wb^2\),考虑证明:\(a+wb^2-(a+wi^2)=w(b^2-i^2)=w(b-i)(b+i)\),这个东西是 \(b+i\) 的倍数,所以得证。
那么对于一组 \(k\) 和 \(b\),一个 \(a\) 要合法一定有 \(a\equiv -wb^2(\bmod\ \text{lcm}\{b,b+1,\cdots,b+k\})\),则方案数就是 \(\lfloor\frac{ma-(-wb^2)}{\text{lcm}}\rfloor+1\),注意这里的 \(-wb^2\) 是在模 \(\text{lcm}\) 意义下的,且注意如果 \(\text{lcm}|(-wb^2)\),那么答案会比这个东西少 \(1\)。
我们对于 \(k\ge 2\) 的,由于 \(\text{lcm}\) 非常大,所以直接暴力算。现在我们只需要考虑 \(k=1\) 的:
同理可以得到对于一个 \(b\) 合法的 \(a\) 的个数是 \(\lfloor\frac{ma-(-wb^2)}{b(b+1)}\rfloor+1\),考虑 \(w\) 不是非常大,我们直接对于 \(b\le 10^6\) 的暴力算,对于 \(b\ge 10^6\) 的,由于 \(w\) 是 \(10^6\) 级别,\(ma\) 是 \(10^18\) 级别,所以答案是 \(10^6\) 级别的,我们可以枚举答案,算出合法的 \(b\) 的个数(可以证明它一定成一段区间,二分即可),那么这部分就是 \(10^6\) 带 \(\log\),常数写好一点即可通过。
0911
[20240911]小K的魔法石
我们首先考虑把初始分数算出来,首先二分,然后我们考虑对于一个 确定的 \(r\),满足条件的 \(l\) 一定是从 \(l_0\sim r\) 的一段连续下标,且如果 \(r_1\le r_2\),则有 \(l_1\le l_2\),所以我们 \(O(n)\) 双指针可求。
考虑如果我们修改了一个位置的值,那么只有跨过这个位置的区间的贡献会被改写,所以我们只需要算跨越中间位置的贡献即可。我们把这些区间拆成这个位置左边的一段后缀和右边的一段前缀,那么不同的区间或值只有 \(O(\log n)\) 种(经典结论),所以我们直接枚举,可以 \(O(1)\) 算贡献,总复杂度为 \(O(n\log n+m\log ^2n)\)。
[20240911]运输计划
我们首先考虑这样一个性质:如果两个区间 \([l_1,r_1],[l_2,r_2]\) 相离,那么它们的方向选择一定是相同的。事实上,只要它们没有包含关系就一定是这样的,所以我们可以把这样的区间缩成一个点。而缩完点之后,如果有一个点完全被另一个点包含,这个点就是另一个点的儿子,不难发现这样形成的实际上是一条链。不妨假设一开始所有点的方向都是顺时针,我们考虑链上如果一个点的方向是逆时针,则它的父亲也必须是逆时针,所以我们的一种合法方案本质上是选择一个断点,它的父亲全部是逆时针,儿子全部是顺时针,那么我们就能 \(O(n)\) 统计了。
现在我们的问题就是如何缩点,这里不加证明地给出区间 \([l_1,r_1],[l_2,r_2](l_1\le l_2)\) 会缩的充要条件就是 \(l_1<l_2\) 且 \(r_1\in (r_2-n,r_2)\)。所以我们用类似线段树优化建图的东西维护即可,代码很好写。
0915
[20240915] 子集数量
不妨假设 \(a\) 递减。
我们首先考虑对于一种长度 \(l\),最大的长度就是取 \(a_{1\sim l}\),而我们每次找到第 \(k\) 大的后继一定是要么把上一次移动的元素向后移动一位,要么就是把上一次一定的元素的前一个元素向后移动一位,所以我们用堆维护一个类 \(k\) 路归并的东西即可。
[20240915] 巧购麦片
我们不妨假设第 \(i\) 个物品的价格为 \(c_i\),贡献为 \(w_i\),且 \(c\) 递减。
那么考虑交换 \(k\) 次一定就是用一个前缀的物品的价格去交换,因为前缀最小,不妨假设我们拿了 \(1\sim i\) 的物品进行交换,换取了 \(j\sim n\) 的物品里的 \(k\) 件的价值,那么假设 \(p_i\) 表示从 \(1\sim i\) 中选出 \(i-k\) 样物品使得价值和最大,\(s_i\) 表示从 \(i\sim n\) 中选出 \(k\) 样物品使得价值和最大,那么我们当前就花了 \(\sum\limits_{t=1}\limits^{i}c_t\) 的代价获得了 \(p_i+s_j\) 的贡献。然后对于 \(i+1\sim j-1\) 这一段的物品,由于它们没有参与交换,我们用朴素的背包跑就可以了。复杂度是 \(O(n^2C)\)。我们考虑如何优化掉一个 \(n\),考虑我们可以去枚举 \(j\),然后把 \(s_j\) 的贡献保留在 \(j\) 上,然后把 \(1\sim i\) 当成一个花费为 \(\sum\limits_{t=1}\limits^{i}c_t\) 贡献为 \(p_i\) 的物品,在背包的时候加入这种把 \(1\sim i\) 打包的转移即可,复杂度就是 \(O(nC)\)。
但是考虑一个问题就是我们之前的那种做法本质上是默认了我们会用完 \(k\) 次交换的,交换次数为 \(0\sim k-1\) 的没有算到。考虑如果出现这种情况说明我们的最优取法只需要取一个前缀和一个后缀就够了,所以 \(j=i+1\),我们就不需要把中间部分拿出来单独背包了,直接算即可,复杂度为 \(n^2\log n\),其中 \(\log n\) 来自于算 \(p,s\) 所需要的堆。
0916
[20240916] 麻将
考虑我们把牌按照值从小到大进行 DP,那么如果我们处理完了 \(1\sim i-1\) 的牌的组合方式,对于后面的牌一定只有 \(i+1,i+2\) 会受到影响,我们可以在 DP 的时候把 \(i+1,i+2\) 被用掉了几张记到状态里面来,进行一个前缀和优化,就能做到 \(O(n^2)\) 了,稍加卡常就能发过掉抽象的 \(n=30000\) 了。
[20240916] 序列
令 \(b\) 为 \(a\) 的差分数组,其中 \(b_{n+1}=-a_n\),那么显然有 \(\left(\sum\limits_{i=1}\limits^{n+1}b_i\right)=0\)。
我们现在每次对一个区间整体减 \(1\) 本质上就是在 \(b\) 上选择两个位置 \(l,r\) 满足 \(l<r\) 且 \(b_l>0>b_r\),让 \(b_l\) 减少 \(1\),\(b_r\) 加上 \(1\),代价就是 \((r-l)^2\),不难发现这个代价函数是满足四边形不等式的,如果要求最大代价就用栈维护匹配,求最小代价就用队列维护即可,是线性的。
[20240916] 骨牌
观察这 \(5\) 种分割方式,我们会发现有些分割最终得到的方案是完全相同的,所以我们现在的问题就是如何去重,如图:
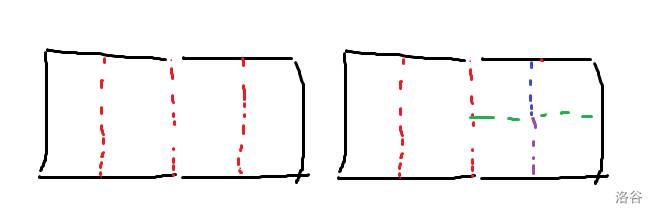
我们让右边的分割和左边的分割不算重只需要强制钦定右边的蓝线和紫线一定有一条没有被分割即可,这个可以容斥算。所以我们可以设状态 \(f_{x,y,k,0/1,0/1}\) 表示左上角是 \((x,y)\),短边长度为 \(2^k\),横着/竖着放的,中间有/没有被限制不能砍断的方案数,DP 即可,复杂度为 \(O(2^{2k}n)\)。
[20240916] 距离
考虑树怎么做,我们直接换根的时候维护每条边被算到的次数即可。
考虑建圆方树怎么做,我们套用树的做法,设从圆点到方点的边权为当前圆点到方点的父亲的最短路,方点到圆点的边权为 \(0\) ,那么这样我们把任意一个圆点当作根,它到所有点的最短路之和就是整棵树的深度之和,我们还是换根维护即可。
0922
距离
最好打对拍,想一想这个题的思路还有没有遗漏的地方。
我们显然有一种暴力的思路就是去直接 \(O(3^k)\) 枚举子集更新,但是这是没有必要的。因为如果 \(x\&y=y,y\& z=z\),那么一定有 \(x\& z=z\),所以我们没有必要去处理 \(x\) 到 \(z\) 的边,每次只需要枚举一个位置的 \(1\) 删掉即可。注意这样做有个问题就是我们还需要存一下每个点是从哪种边来的,因为假如有 \(x\&y =y,y\& z=z\),我现在在用 \(y\) 更新 \(z\),那么我会把 \(dis(z)\) 设为 \(dis(y)+1\),但由于 \(y\) 是用相同的边从 \(x\) 过来的,所以我们可以一步到达 \(z\),所以应该是 \(dis(z)=dis(y)\)。当然在从两种边过来的距离相同的情况下肯定优先选择用子集的边更优。
洗牌
排序题从各种排序手法入手(插排、快排、归并、桶排),类似的
考虑这个操作的本质:可以视为我们每次选若干个不交的区间,翻转它们,最后进行一个整体翻转。
那么我们考虑分治地去做这个东西,假如我现在要把区间 \([l,r]\) 排列好,然后一个位置 \(p\) 是 \(1\) 当且仅当 \(a_p>mid\),我们考虑每次操作可以合并两段 \(1\),比如 \(111000111\),我翻转 \(1\sim 6\), 就会变成 \(000111111\),变成一段 \(1\) 了。并且我们是可以在一次操作同时合并多组 \(1\) 的,所以我们可以对于分治的深度相同的每一层可以同时做这个操作,那么我的操作数就是 \(O(\log ^2 n)\) 的。
抽卡
神必题,考试不该做这道的。
首先把 \(a\) 按照从大到小排序。
如果我们一次操作种抽到了 \(a_i\),如果我接受了它,那么对于任意 \(j<i\),我也会接受它;如果我扔掉了它,那么对于任意 \(j>i\),我也会扔掉它。所以我可以把这样的决策抽象成一个决策点 \(j\),对于 \(i\le j\) 我接受它,否则我扔掉它。
我们不加证明地给出一个性质:假如我当前的决策点是 \(j\),我以后的决策点一定单调不增。
所以我们就能够把 \(j\) 当成一个中间量放到 DP 外面去,复杂度为 \(O(qn)\)。
最小生成树
完全做不来。
考虑边权非常小,我们可以设 \(s_{i,j}\) 表示只用边权不超过 \(j\) 的,把 \(1\sim i+1\) 尽可能连通要连多少条边,那么 \(ans_i=\sum\limits_{j=0}\limits^{30}s_{i,j}\)。
现在问题就变成了边权为 \(1\) 但有可能不连通,考虑维护。假设我们要从 \(i\) 层扩展到 \(i+1\) 层,那么首先显然我们可以把 \(i-1\) 层和 \(i\) 层之间的连边 copy 过来,然后我们考虑能否合并一些连通块,我们每合并一块这一层的边数就会减少 \(1\),那么我们最后对这个东西做一遍前缀和即可。
我闷如果每次暴力去判断每一条边,那么复杂度就是 \(O(30n^2\alpha)\)。考虑我们只有在合并两个连通块的时候才有可能继续合并两个连通块,所以我们维护一下在上一层新连通的连通块所对的连通块即可,复杂度为 \(O(n)\)。
0928
伐木
直接换根 DP,完了。
面积
跑出来以 \(a_i\) 为最小值的左右边界,然后二分出答案,用 k 路归并跑第 \(L\sim R\) 元素即可。
排列
设 \(a_{1\sim n}\) 为点 \(1\sim n\),\(b_{1\sim n}\) 为点 \(n+1\sim 2n\)。
考虑对于 \(a_i=b_j\),从 \(i\) 向 \(j\) 连边。
1008
风花雪月
考虑我们设一个 DP 状态表示所有刚好可以得到 \(n\) 种元素的期望。那么它的值就应该是到这个状态的概率乘上抽取次数。这个 DP 是 \(O(nm^2)\) 的,但是带 \(2\) 的常数。我们考虑设状态为所有还没有凑到 \(n\) 种元素的期望,最后用总数减,这样就能通过了。
镜子
考虑直接跑最短路肯定是过不了的,我们考虑对连通的最长的行和列建点,不难发现如果是表示第 \(i\) 行的 \([l,r]\) 的行点,那么到这里一定是从上面走下来的,即一定是从一个列点走下来的,所以我们会从所有和它有交的列点向它连双向边,这一步用主席树优化建图即可,对于列点是同理的。这一步是 \(O(n\log n)\) 的。
我们算最短路用 01bfs 算即可。
那么我们计算答案可以算每个行点的长度乘上它的距离,但是有个问题就是有些行点与列点有交,交的这些点的距离是行列点距离的 \(\min\),所以我们还需要维护某个区间某种值的个数,然后这里有个很好的性质,如果行点 \([l,r]\) 的距离为 \(x\),那么和它有交的列点的距离 \(x'\) 一定满足 \(|x'-x|\le 1\),所以我们在里面维护值只需要用一个三元组维护即可,复杂度是 \(O(n\log n)\) 的。
1010
拼串
考虑我们每次放一个串 \(A\) 的合法条件是上一次放的串 \(A'+A[0]\) 在 \(T\) 中未出现过,这启示我们去快速算出 \(f_{0\sim 3,0\sim 3}\) 表示从 A/B/C/D 字符转移到 A/B/C/D 字符的最短长度,这个东西用 SAM 随便算一下就行了。
考虑我们本质上是想用最多的次数拼出长度为 \(n\) 的,这个东西不是特别好做,我们可以去二分次数,然后判断用这么多次所拼出的最长长度是否大于等于 \(n\)。这个东西可以用矩阵加速去 DP,所以复杂度是 \(O(|T|^3\log n)\)。
随机串
我们不妨钦定 \(s_{a_1}=s_{a_2}=\cdots =s_{a_k}=0\),最后给概率乘 \(2\) 即可。
考虑两种情况:
- \(0\) 先用完,假设是在位置 \(i\in (a_k,2n)\) 用完的,那么概率就是 \(C_{i-1}^{n-1-k}\times 2^{-i}\),假设 \(i=a_k\),那么概率就是 \(C_{i-1}^{n-k}\times 2^{-i}\)。
- \(1\) 先用完,那么假设是在位置 \(i\neq a_j\),假设 \(i\) 前面有 \(t\) 个 \(a\),那么概率就是 \(C_{i-1-t}^{n-1}\times 2^{-i}\),假设是在位置 \(i=a_j\),那么概率为 \(0\)。
所以我们的问题本质上就是求 \(\sum\limits_{i=l}\limits^{r}C_{i-1}^{n-k}\times 2^{-i}\) 和 \(\sum\limits_{i=l}\limits^{r}C_{i-1-t}^{n-1}\times 2^{-i}=2^{t+1}\sum\limits_{i=l-t-1}\limits^{r-t-1}C_{i}^{n-1}\times 2^{-i}\),这个东西显然用前缀和做即可,问题在于前面那个东西。
设这个东西的值为 \(f(k,l,r)\),把它映射到杨辉三角上去发现 \(f(k,l,r)=f(k-1,l,r)+O(1)\),所以我们可以 \(O(k)\) 算这个式子。所以总复杂度就是 \(O(n+\sum k)\)。
俄罗斯方块
设 \(b_{0\sim k-1}\),\(b_i=\sum\limits_{j\bmod k=i}(a_j\bmod k)\),那么有解的充要条件就是 \(b_{0}\sim b_{(n\bmod k)-1}\) 完全相等且 \(b_{(n\bmod k)}\sim b_{k-1}\) 完全相等。
- 通过放竖块的方式让 \(a_{0\sim n-1}\) 的长度单调不降。
- 通过放横块的方式把所有位置的高度都搞成 \(a_{n-1}\)。
- 通过上面那一步得到的 \(a_{k-1}\sim a_{n-1}\) 长度一定都相等,我们通过不断往 \(a_{0\sim k-2}\) 插竖块的方式来把 \(a_{k-1}\sim a_{n-1}\) 消成 \(0\)。
- 此时一定有 \(b_{k-1}=0=b_{k-2}=\cdots=b_{(n\bmod k)}\),所以 \(a_{(n\bmod k)\sim a_{k-2}}\) 都是 \(k\) 的倍数,我们可以直接通过插入若干个竖块来消掉。
- 所以我们现在只剩下 \(a_{0}\sim a_{(n\bmod k)-1}\) 没有消完了,由于后面都是空的且空的长度是 \(k\) 的倍数,所以我们可以先把左边补齐再通过放横块的方式来消完。
1012
染色
如图:
扫雷
1013
序列划分
1023
[20241023] 修路
设状态 \(f_{i,S}\) 表示以 \(i\) 为中心,当前为 \(S\) 点集的点的生成树的最小值,那么我们设 \(S'=S-\{i\}\),去枚举 \(T\subset S'\),枚举 \(T\) 的中心 \(j\),从 \(f_{i,S-T}\) 和 \(f_{j,T}\) 转移过来即可,本质上是在枚举子树。注意到根有可能是叶子,所以再记一维 \(0/1\) 表示中心有几个儿子即可。
1029
<20241029>「eJOI2021」二分查找
很简单,观察大样例即可发现规律。
<20241029>「eJOI2021」河畔
这个题的大样例很水,导致乱贪可以过所有大样例。
正解是先二分,考虑计算出每棵树至少需要剪多少次,然后每次每棵树能剪就剪,这样做比较显然是对的。但是暴力实现是 \(O(nm\log n)\) 的。考虑用一个东西维护当前可以被剪的所有树,这样做复杂度就是 \(O(n+mk)\log n\)。
<20241029>「JOISC 2017 Day 1」港口设施
这个题的大样例也很水,导致乱猜的结论可以过所有大样例。
结论是奇环大小最多为 \(3\),但是会发现显然有可能存在大小为 \(5\) 的奇环。所以我们可以拿线段树优化建图,在建图过程中用扩展域并查集维护奇环情况,复杂度为 \(O(n\log n)\)。
<20241029>「POI2020 R1」Gra platformowa
这个题的大样例比较水,但是它写明了,而且我相信区区一个 bfs 复杂度不可能写假,就导致了 swap 两个 \(O(n)\) 的数组 \(n\) 次的悲剧,和之前 strlen \(n\) 次有异曲同工之妙。
思路很简单,直接按照题目的要求建图,用一个虚点把所有终点连起来跑一个单源最短路即可。由于边权只有 \(0/1\),时间复杂度为 \(O(n)\)。
总结
总结是 T3 做得太急了,导致时不时拍出来几组错,导致花了很久时间来修,间接导致没有时间给 T4 测极限大样例,导致 T4 全 T 了。
下次可以在最后半个小时不要再写题了,集中精力去检查前面的题。
标签:blue,limits,记录,color,省选前,传送门,green,我们,模拟 From: https://www.cnblogs.com/Judgelight/p/18514323