首先,我们关注一下“相似”是什么意思:它等价于,两个字符串中 B 和 N 的数量分别相同。
显然地我们可以发现,每次操作,相当于给字符串加或减一个 B 或 N 或 BN。
把每个字符串中 B 的个数作为横坐标,N 的个数作为纵坐标,找到其对应点。
那么,每次操作,就相当于把这个点的位置往左或右或上或下或右上或左下移动一步,如下图。
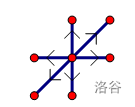
由于两个点都操作和仅操作一个点没有区别,因此,等价于我们要找到一个点 \(T\),其到 \(n\) 个点的距离的最大值最小。
显然想到二分,因此只需要判断距离 \(n\) 个点 \(l\) 的区域有没有交集即可。
观察可知,这个区域长下面这样:

如何限定这个区域呢?由于它是凸的,所以可以用线性规划描述,如下图
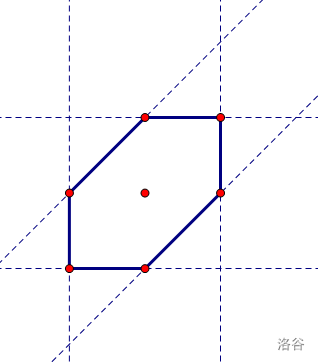
即可得到六个限制条件
\[\left\{\begin{matrix} x\le x_0+l \\ x\ge x_0-l \\ y\le y_0+l \\ y\ge y_0-l \\ x-y\le x_0-y_0+l \\ x-y\ge x_0-y_0-l \end{matrix}\right.\]将 \(n\) 个限制条件取交集,就可以得到 \(x,y,x-y\) 分别的取值范围。
假设 \(x\in[xi,xa],y\in[yi,ya],x-y\in[zi,za]\)(这里 \(i,a\) 分别是 \(\min,\max\) 的简写),那么:
- 三个区间如果有任意一个为空,则不成立
- 假如三个都非空,则若 \([xi-ya,xa-yi]\) 与 \([zi,za]\) 不相交则不成立,否则成立
现在只需要构造答案了。
假设我们如上求出了 \(x,y,x-y\) 的范围,那么显然有 \(x \in[yi+zi,ya+za]\),与 \([xi,xa]\) 取交集后求出 \(x\) 的一个值,然后便有 \(y\in[x-za,x-zi]\),与 \([yi,ya]\) 取交集后求出 \(y\) 的一个值,即可。
Code:
#include <bits/stdc++.h>
using namespace std;
const int N = 300005, M = 500005, inf = 0x3f3f3f3f;
int n;
int x[N], y[N];
char s[M];
void chkmax(int &a, int b) { if (a < b) a = b; }
void chkmin(int &a, int b) { if (a > b) a = b; }
bool check(int cur) {
int Lx = -inf, Rx = inf, Ly = -inf, Ry = inf, Lz = -inf, Rz = inf;
for (int i = 1; i <= n; ++i) {
chkmax(Lx, x[i] - cur), chkmin(Rx, x[i] + cur);
chkmax(Ly, y[i] - cur), chkmin(Ry, y[i] + cur);
chkmax(Lz, x[i] - y[i] - cur), chkmin(Rz, x[i] - y[i] + cur);
}
chkmax(Lx, 0), chkmax(Ly, 0);
if (Lx > Rx || Ly > Ry || Lz > Rz) return false;
if (Lx - Ry > Rz || Rx - Ly < Lz) return false;
return true;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%s", s + 1); int len = strlen(s + 1);
for (int j = 1; j <= len; ++j) {
if (s[j] == 'B') ++x[i];
else ++y[i];
}
}
int l = 0, r = 500001;
while (l < r) {
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
printf("%d\n", l);
int Lx = -inf, Rx = inf, Ly = -inf, Ry = inf, Lz = -inf, Rz = inf;
for (int i = 1; i <= n; ++i) {
chkmax(Lx, x[i] - l), chkmin(Rx, x[i] + l);
chkmax(Ly, y[i] - l), chkmin(Ry, y[i] + l);
chkmax(Lz, x[i] - y[i] - l), chkmin(Rz, x[i] - y[i] + l);
}
chkmax(Lx, 0), chkmax(Ly, 0);
int ans1 = min(Rx, Ry + Rz), ans2 = min(ans1 - Lz, Ry);
for (int i = 1; i <= ans1; ++i) putchar('B');
for (int i = 1; i <= ans2; ++i) putchar('N');
return 0;
}