标签：总结系列 Point double another return Line public

1.前言

由于好几次作业都是采用同一个包里面的类，期间经过了好几次的重构，特别是抽离了父类之后，可能只适应于最后一次的作业。

2.类

2.1 Point

attribute:

对于Point来说，两个属性（x , y）即可

function:

add(Point)

两个点的加法运算，对应坐标相加，并返回一个新的Points
print()

打印点的一些信息，用于debug
isSameTo(Point)

判断两个点是否一样，返回true/false
disToLine(Line)

求出点到直线的距离，使用距离公式，返回值double
inLine(Line)

判断点是否在直线上，返回true/false
disToPoint(Point)

求两点距离，返回double
focusPoint(Points[])

求出点集的重心，重心公式，返回double
deepCopy()

深拷贝一个Point,返回新的Point
sub(Point)

两个点的减法运算，对应坐标相减，返回新的Point
inLineSegment_close(Line)

判断点是否在线段之内，包括端点，返回true/false
inLineSegment(Line)

判断点是否在线段之内，不包括端点，返回true/false

对应类图：

code:

package Points;

public class Point{
    public double x, y;

    public Point(){
        this.x = 0;
        this.y = 0;
    }
    public Point(double a,double b){
        this.x = a;
        this.y = b;
    }

    public void print(){
        String x = String.format("%.6f",this.x);
        String y = String.format("%.6f",this.y);
        x = x.replaceAll("0+?$", "");
        y = y.replaceAll("0+?$", "");
        System.out.printf("(%s , %s)\n",this.x,this.y);
    }

    //两点坐标相同
    public boolean isSameTo(Point a){
        return (this.x == a.x)&&(this.y == a.y);
    }
    //两点距离
    public double disToPoint(Point another){
        return Math.sqrt(Math.pow(this.x-another.x,2) + Math.pow(this.y-another.y,2));
    }
    //点到直线的垂直距离
    public double disToLine(Line l){
        return Math.abs(l.a*this.x+l.b*this.y+l.c) / Math.sqrt(Math.pow(l.a,2)+Math.pow(l.b,2));
    }
    //判断是否在直线之上
    public boolean inLine(Line l){
        return Math.abs(l.a*this.x + l.b*this.y + l.c) < 0.000001;
    }
    //判断是否在线段之内(包括端点)
    public boolean inLineSegment_close(Line l){
        if(!this.inLine(l)) return false;
        double res = this.disToPoint(l.sta) + this.disToPoint(l.ed) - l.length();
        return Math.abs(res) < 0.000001;
    }
    //判断是否在线段之内（不包括端点）
    public boolean inLineSegment(Line l){
        return this.inLineSegment_close(l) &&
                (!this.isSameTo(l.sta)) &&
                (!this.isSameTo(l.ed));
    }
    public Point deepCopy(){
        Point res = new Point();
        res.x = this.x;
        res.y = this.y;
        return res;
    }

    public Point add(Point another){
        Point res = this.deepCopy();
        res.x += another.x;
        res.y += another.y;
        return res;
    }

    public Point sub(Point another){
        Point res = this.deepCopy();
        res.x -= another.x;
        res.y -= another.y;
        return res;
    }


    //求点集重心
    public static Point focusPoint(Point[] points ){
        Point res = new Point(0,0);
        for(Point item:points){
            res = res.add(item);
        }
        res.x /= points.length;
        res.y /= points.length;
        return res;
    }

}

2.2 Line

attribute:

采用一般式：AX + BY + C = 0 的形式描述直线

Point sta,ed 两者为直线上不同的两个点

Point vector 为sta-ed 代表向量

function:

isParallelTo(Line)

判断两条直线是否相互平行，返回true/false
lsi(Line) //LineSegmentIntersection

求两条线段的交点，返回Point,无交点则返回null
isVerticalTo(Line)

判断两直线是否相互垂直
vectorAngle(Line)

求vector属性的夹角，返回double
print()

打印直线的某些信息，用于debug
vectorMul(Line)

求vector属性的点乘，返回double
vectorCrossMul(Line)

求vectoe属性的叉乘，返回double
length()

求线段长度，返回double
getIntersection(Line)

求两条直线的交点，返回Point,无交点则返回null
slope()

求直线的斜率，返回double
isSameTo(Line)

判断两条直线是否平行，返回true/false
vectorLength(Line)

求vector属性的长度，返回double

对应类图：

code:

package Points;

public class Line{
    public Point sta, ed;
    public double a,b,c;
    private final Point vector;

    public Line(Point a,Point b)throws Exception{
        if(a.isSameTo(b)){
            throw new Exception("points coincide");
        }
        this.sta = a;
        this.ed = b;
        this.a = (-(a.y-b.y));
        this.b = (a.x-b.x);
        this.c = (-this.a*this.sta.x-this.b*this.sta.y);
        this.vector = ed.sub(sta);
    }

    public void print(){
        System.out.printf("%fX + %fY + %f = 0\n",this.a,this.b,this.c);
    }

    //求线段长度
    public double length(){
        return this.sta.disToPoint(this.ed);
    }

    //求线段斜率
    public double slope(){
        if(this.b == 0){
            return 2^48;
        }
        return -this.a / this.b;
    }

    //判断是否平行
    public boolean isParallelTo(Line another){
        if(this.b==0 || another.b==0){
            return (this.b == 0 && another.b == 0);
        }
        return ((this.a / this.b) == (another.a / another.b));
    }

    //判断是否重合
    public boolean isSameTo(Line another){
        return this.isParallelTo(another) && (this.sta.inLine(another));
    }

    //判断是否垂直
    public boolean isVerticalTo(Line another){
         return this.a * another.a + this.b * another.b == 0;
    }
    //求两条直线交点
    public Point getIntersection(Line another){
        if(this.isParallelTo(another)) return null;
        Point res = new Point();
        res.y = (another.a*this.c-this.a*another.c) / (this.a*another.b-another.a*this.b);
        res.x = (this.b*another.c-another.b*this.c) / (this.a*another.b-another.a*this.b);
        return res;
    }

    //LineSegmentIntersection 获取线段交点，返回值可能为null
    public Point lsi(Line another){
        Point res = this.getIntersection(another);
        if(res == null) return res;
        boolean ok = (res.inLineSegment_close(this) && res.inLineSegment_close(another));
        return ok ? res:null;
    }

    /*---------------------------------------------分割线-------------------------------------------------------------*/
    /*---------------------------------------------分割线-------------------------------------------------------------*/
    /*---------------------------------------------分割线-------------------------------------------------------------*/
    //求向量模
    public double vectorLength(){
        return Math.sqrt( Math.pow(this.vector.x,2) + Math.pow(this.vector.y,2) );
    }
    //求向量点积
    public double vectorMul(Line another){
        return (this.vector.x * another.vector.x) + (this.vector.y * another.vector.y);
    }

    //求向量叉积
    public double vectorCrossMul(Line another){
        return (this.vector.x * another.vector.y) - (another.vector.x * this.vector.y);
    }
    //求两向量夹角(非0向量)
    public double vectorAngle(Line another){
        double cos_angle = this.vectorMul(another) / (this.vectorLength() * another.vectorLength());
        return Math.acos(cos_angle);
    }

}

2.3 Graphical

attribute:

对于三角形，四边形，五边形...这些多边形的父类---图形类，抽离出一些统一的属性：

构成图形的点 points；
构成图形的线 lines；
面积 area；
周长 sidelength；
凹凸性 isConvexGraphical；
为了管理这些属性，添加一个len属性作为points,lines属性的长度
添加一些控制信息：

图形状态 status（标记是否构成了多边形）;
状态信息 message（不构成图形的原因）

function:

Graphical(Point[])

析构函数接受一个Points数组参数
1. 对points数组进行出重操作,如果去重之后点数不足2，则结束构造，设置status = -1 设置 message = “Not enough points”
2. 对于points数组中的连续三个元素P1P2P3，如果向量P1P2 和向量P2P3的夹角为0度则去除P2点，如果为180度则结束构造，设置status = -1 设置message = “lines reverse coincidence”
3. 开始赋值lines属性，并判断不相邻的line是否有交点，如果有交点则设置 status = -1 设置message = “Non adjacent edges have intersections”
4. 设置属性area sidelength isConvexGraphical 的值，正常结束构造
area(Graphical)

对于求任意多边形的面积，同样是分割成不同的三角形然后求和，但是考虑到凹多边形特殊性求三角形面积采用向量的叉乘。
以原点为参考点O，相邻顶点P1,P2,求：

按{P1, P2, P3, P4, P5}顺序求出OP1×OP2 ,OP2×OP3… 求和即可
sideLength(Graphical)

对Lines属性的length属性求和即可
isConvexGraphical(Graphical)

我们知道向量叉乘是有正负的，对于下面的向量，我们求OP1 × OP2，结果是正，而反过来求叉乘则是负，直观来看就是：
P1在向量OP2的左侧则叉乘为正，P2在向量OP1的右侧则叉乘为负。

假设当前连续的三个顶点分别是P1，P2，P3。计算向量（P1，P2）,（P1，P3）的叉乘，也就是计算三角形P1P2P3的面积，得到的结果如果大于0，则表示P2点在线段P1和P3的右侧，多边形的顶点是逆时针序列。然后依次计算下一个前后所组成向量的叉乘，如果在计算时，出现负值，则此多边形时凹多边形，如果所有顶点计算完毕，其结果都是大于0，则多边形时凸多边形。
isContainPoint(Point)

判断图形是否包含某一个点

首先特判在边上的情况！

假设点位于多边形内部：

显然以P为顶点为顶点的三角形面积和等于多边形面积

假设点位于多边形外部：

显然以P为顶点的三角形面积和不等于多边形面积
isSeparatedFrom(Graphical)

判断两个图形是否完全分离
两个图形重叠面积为0 + 点都不在对方的边上
isContainGra(Graphical)

判断一个图形this是否完全包含另一个图形g
g图形的所有点都位于this图形内部或者边上
isSameTo(Graphical)

判断两个图形是否相同
relationshipWith(Graphical)

判断两图形之间的关系
判断优先级：分离，完全重合，包含，被包含，连接，交错
其中前四者都有对应函数实现
判断连接还是交错，只需看有没有重叠面积就行
overlappingArea(Graphical)

求两个图形的重叠面积

请先观察下面的图形：

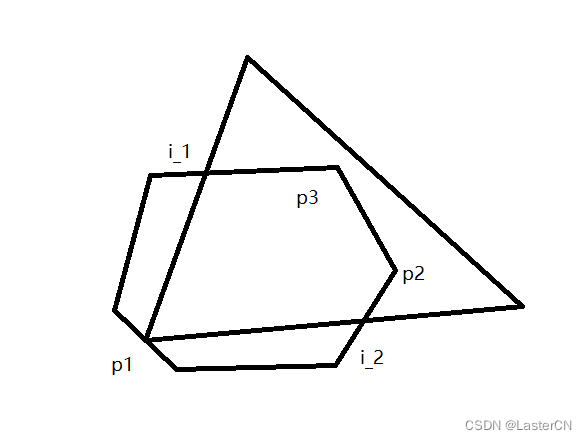
在这里插入图片描述

不知道是否观察出，重叠部分的多边形，他的顶点由，两个图形边的交点和部分顶点构成
假设我们求出了这些交点和顶点构成数组intersection = { P1, I2, P2, P3, }，并按照一定的顺序排序，使得该数组按顺序可以构成多边形，那么求出这个多边形的面积则是两个图形的重叠面积

图形的交点：
暴力枚举两图形的lines求解
部分顶点
同样可以由上图观察出，这些顶点必然会出现在另一个图形的内部
排序：
提供两种思路
1. 求出这些点集intersection的重心，任选一个点集中的点与重心构成参考向量(OP1)：
  
  则不同向量OPx和参考向量OP1的夹角不相同，如果根据这些角度的大小对这些点集进行排序，最终会得到以P1开始，逆时针遍历的集合{ P1, P2, P3, P4, P5 }；
  根据这个集合就可以构成一个多边形了
2. 首先会有两个集合，一个集合为上诉点集A = { P1, P5, P2, P3, P4 }，一空集B = { }；
  同样选择一个参考点P1，之后A集合去除P1，B集合加入P1 变成：
  A = { P5, P2, P3, P4 } B = { P1 }
  {
  遍历A集合，求出与B集合末尾元素(P1)最近的点Px;
  A = A - Px ; B = B + Px
  }
  重复上诉大括号内的步骤，直到A集合为空
  得到的B集合则一定可以构成多边形

前一个思路凹凸多边形都适用，后者只适用于凸多边形

对应类图:

code:

package Points;

import java.util.Arrays;
import java.util.Comparator;

public class Graphical {
    public int len=0,status=1;    //多边形边数,状态
    public Point[] points;
    public Line[] lines;
    public double sideLength = 0,area = 0;   //边长,面积
    public boolean isConvexGraphical = true;
    public  String message = "init"; //信息

    public Graphical(Point[] points){
        this.points = new Point[points.length];

        points = this.removeMulti(points);  //去除重复点
        if(points.length <=2 ){
            this.status = -1;
            this.message = "Not enough points";
            return;
        }

        //相邻边夹角0则去除中间点，夹角180则status:-1
        for(int i=0;i<points.length;i++){
            int first = i , second = (i+1)%points.length, third = (i+2)%points.length;
            try{
                Line l1 = new Line(points[first],points[second]);
                Line l2 = new Line(points[second],points[third]);
                if( Math.abs(l1.vectorAngle(l2) - Math.PI) < 0.000001 ){    //夹角180
                    this.status = -1;
                    this.message = "lines reverse coincidence";
                    return;
                }
                else if(Math.abs(l1.vectorAngle(l2)) > 0.000001){   //夹角不为0
                    this.points[this.len++] = points[second].deepCopy();
                }
            }catch (Exception e){}
        }

        this.points = Arrays.copyOf(this.points,this.len);
        this.lines = new Line[this.len];

        //初始化边
        for(int i=0;i<this.len;i++){
            try {
                int first = i, second = (i+1)%this.len;
                this.lines[i] = new Line(this.points[first], this.points[second]);
            }catch (Exception e){}
        }

        //判断任意不相邻边(线段交点)是否有交点
        checkEdge();

        Graphical.area(this);
        Graphical.sideLength(this);
        Graphical.checkConvex(this);
    }
    public void print(){
        if(this.status == -1){
            System.out.println(this.message);
            return;
        }
        System.out.println("点数为："+this.len);
        for(int i=0;i<this.len;i++){
            this.points[i].print();
        }
        for(int i=0;i<this.len;i++){
            this.lines[i].print();
        }
        System.out.println("周长为："+this.sideLength);
        System.out.println("面积为："+this.area);
        System.out.println("凹凸性："+this.isConvexGraphical);
    }
    //判断图形是否包含某个点返回值-1,0,1 (内部，边缘，外部)
    public int isContainPoint(Point p){
        for(int i=0;i<this.len;i++){    //位于边之上
            if(p.inLineSegment_close(this.lines[i])) return 0;
        }

        double s = 0;
        for(int i=0;i<this.len;i++){
            s += Triangle.area(p,this.points[i], this.points[(i+1)%this.len]);
        }
        return Math.abs(s-this.area) < 0.000001 ? -1:1;
    }
    //判断两个图形类之间的关系()
    public String relationshipWith(Graphical g){
        String[] name = new String[]{"triangle", "quadrilateral", "pentagon"};
        //分离
        if(this.isSeparatedFrom(g)){
            return "no overlapping area between the previous "+name[this.len-3]+ " and the following "+name[g.len-3];
        }
        //完全重合
        if(this.isSameTo(g))
            return "the previous "+name[this.len-3]+ " coincides with the following "+name[g.len-3];
        //包含
        if(this.isContainGra(g)){
            return "the previous "+name[this.len-3]+ " contains the following "+name[g.len-3];
        }
        //被包含
        if(g.isContainGra(this)){
            return "the previous "+name[this.len-3]+ " is inside the following "+name[g.len-3];
        }

        //连接
        if(this.overlappingArea(g) == 0){
            return "the previous "+name[this.len-3]+ " is connected to the following "+name[g.len-3];
        }

        //交错
        return "the previous "+name[this.len-3]+ " is interlaced with the following "+name[g.len-3];

    }

    //判断和另一个图形完全分离(重叠面积为0，并且任意点都在this之外)
    public boolean isSeparatedFrom(Graphical g){
        boolean ok = true;
        int[] check2 = new int[g.len];
        for(int i=0;i<g.len;i++){
            check2[i] = this.isContainPoint(g.points[i]);
        }
        for(int item:check2){
            if(item != 1) ok = false;
        }
        if(this.overlappingArea(g) !=0) ok = false;
        return ok;
    }
    //判断完全包含另一个图形（任意点都在this之内）
    public boolean isContainGra(Graphical g){
        boolean ok = true;
        int[] check2 = new int[g.len];
        for(int i=0;i<g.len;i++){
            check2[i] = this.isContainPoint(g.points[i]);
        }
        for(int item:check2){
            if(item == 1) ok = false;
        }
        return ok;
    }
    //判断两个图形是否一模一样(点完全重合)
    public boolean isSameTo(Graphical g){
        if(this.len != g.len) return false;
        for(int i=0;i<this.len;i++){
            boolean ok = false;
            for(int j=0;j<g.len;j++){
                if(this.points[i].isSameTo(g.points[j])) ok = true;
            }
            if(!ok) return false;
        }
        return true;
    }

    //计算两个图形的重叠面积(交点加内部顶点构成重叠多边形)
    public double overlappingArea(Graphical g){
        Point[] intersection = new Point[100];
        int intersection_len = 0;


        for(Line item1:this.lines){   //求出两多边形的交点
            for(Line item2: g.lines){
                Point tmp = item1.lsi(item2);
                if(tmp != null){
                    intersection[intersection_len++] = tmp.deepCopy();
                }
            }
        }

        for(Point item:g.points){   //顶点包含在内部
            if(this.isContainPoint(item) == -1) intersection[intersection_len++] = item.deepCopy();
        }
        for(Point item:this.points){   //顶点包含在内部
            if(g.isContainPoint(item) == -1) intersection[intersection_len++] = item.deepCopy();
        }

        if(intersection_len ==0 ) return 0;


        /*排序交点数组*/
        intersection = Arrays.copyOf(intersection,intersection_len);
        intersection = this.removeMulti(intersection);
        Point focus = Point.focusPoint(intersection);
        Point sta = intersection[0].deepCopy();

        Arrays.sort(intersection,1,intersection.length, new Comparator<Point>()  {
            @Override
            public int compare(Point o1, Point o2) {
                try{
                    Line origin =new Line(focus,sta);
                    Line l1 = new Line(focus,o1);
                    Line l2 = new Line(focus,o2);
                    double angle1 = origin.vectorAngle(l1);
                    double angle2 = origin.vectorAngle(l2);
                    if(origin.vectorCrossMul(l1) < 0) angle1 = 2*Math.PI - angle1;
                    if(origin.vectorCrossMul(l2) < 0) angle2 = 2*Math.PI - angle2;
                    if(angle1-angle2 > 0.000001) return 1;
                    if(Math.abs(angle1-angle2) < 0.000001) return 0;
                    return -1;
                }catch (Exception reason){}
                return 0;
            }
        });

        Graphical graphical = new Graphical(intersection);
        return  graphical.area;

    }

    //去除所有重复点
    private Point[] removeMulti(Point[] points){
        Point[] tmp_points = new Point[points.length];
        int tmp_len = 0;

        for(int i=0;i<points.length;i++){
            boolean ok = true;
            for(int j=0;j<tmp_len;j++){
                if(points[i].isSameTo(tmp_points[j])){
                    this.message = "points coincide";
                    ok = false;
                    break;
                }
            }
            if(ok) tmp_points[tmp_len++] = points[i].deepCopy();
        }
        return Arrays.copyOf(tmp_points,tmp_len);
    }
    //判断不相邻边是否有交点
    private void checkEdge(){
        for(int i=0;i<this.len;i++){
            for(int j=i+2;j<this.len;j++){
                if(i==0&&j==this.len-1) continue;
                Point p = this.lines[i].getIntersection(this.lines[j]);
                if(p==null) continue;

                if(p.inLineSegment_close(this.lines[i]) && p.inLineSegment_close(this.lines[j])){
                    this.status = -1;
                    this.message = "Non adjacent edges have intersections";
                    return;
                }
            }
        }
    }
    //多边形面积
    private static void area(Graphical e){
        double res = 0;
        Point origin = new Point(0,0);
        for(int i=0;i<e.len;i++){
            try{
                Line l1 = new Line(origin,e.points[i]);
                Line l2 = new Line(origin,e.points[(i+1)%e.len]);
                res += 0.5 * l1.vectorCrossMul(l2);
            }catch (Exception reason){}

        }
        e.area = Math.abs(res);
    }
    //多边形周长
    private static void sideLength(Graphical e){
        double res = 0;
        for(int i=0;i<e.len;i++){
            res += e.points[i].disToPoint(e.points[(i+1)%e.len]);
        }
        e.sideLength = res;
    }
    //多边形凹凸性
    private static void checkConvex(Graphical e){
        if(e.len == 3) return;
        int v = 0;
        for(int i=0;i<e.len;i++){
            int first = i, second = (i+1)%e.len, thrid = (i+2)%e.len;
            try{
                Line l1 = new Line(e.points[first], e.points[second]);
                Line l2 = new Line(e.points[first], e.points[thrid]);
                if(v==0){
                    if(l1.vectorCrossMul(l2) > 0) v = 1;
                    else v = -1;
                }
                if(v == 1 && l1.vectorCrossMul(l2) < 0) e.isConvexGraphical = false;
                if(v == -1 && l1.vectorCrossMul(l2) > 0) e.isConvexGraphical = false;
            }catch (Exception reason){}
        }
    }


}

2.4 Quadrilateral

extends:

Graphical

attribute:

null

function:

isDiamond()

判断是否是菱形，平行四边形+四边长度相等返回true/false
isParallelQuadrilateral()

判断是否是平行四边形，任意对边平行即可，返回true/false
isSquare()

判断是否是正方形，菱形+矩形，返回true/false
isRectangle()

判断是否是矩形，对角线长度相等，返回true/false
Quadrilatera(Points[])

构造函数，接受点集作为参数，先构造父类，根据父类的status和len属性判断是否可以构成四边形

不能构成四边形抛出异常

对应类图:

code:

package Points;

public class Quadrilateral extends Graphical{

    public Quadrilateral(Point[] points)throws Exception{
        super(points);
        if(this.status == -1 || this.len != 4){
            throw new Exception("not a quadrilateral");
        }
    }

    //判断是否为平行四边形（对边分别平行）
    public boolean isParallelQuadrilateral(){
        return this.lines[0].isParallelTo(this.lines[2]) &&
                this.lines[1].isParallelTo(this.lines[3]);
    }

    //判断是否为菱形（平行四边形 + 四边长度相等）
    public boolean isDiamond(){
        boolean v = this.lines[0].length() == this.lines[1].length() &&
                    this.lines[1].length() == this.lines[2].length() &&
                    this.lines[2].length() == this.lines[3].length();
        return this.isParallelQuadrilateral() && v;
    }

    //判断是否为矩形（对角线相等）
    public boolean isRectangle(){
        return  this.points[0].disToPoint(this.points[2]) == this.points[1].disToPoint(this.points[3]);
    }

    //判断是否为正方形(菱形 + 矩形)
    public boolean isSquare(){
        return this.isDiamond() && this.isRectangle();
    }


}

2.5 Pentagon

extends:

Graphical

attribute:

null

function:

Pentagon(points[])

构造函数，接受点集作为参数，先构造父类，根据父类的status和len属性判断是否可以构成四边形

不能构成五边形抛出异常

对应类图:

code:

package Points;

public class Pentagon extends Graphical {

    public Pentagon(Point[] points)throws Exception{
        super(points);
        if(this.status == -1 || this.len != 5){
            throw new Exception("not a pentagon");
        }
    }


}

3.设计与分析

3.1 点线形系列4-凸四边形的计算

题目描述：

用户输入一组选项和数据，进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入四个点坐标，判断是否是四边形、平行四边形，判断结果输出true/false，结果之间以一个英文空格符分隔。
2：输入四个点坐标，判断是否是菱形、矩形、正方形，判断结果输出true/false，结果之间以一个英文空格符分隔。若四个点坐标无法构成四边形，输出"not a quadrilateral"
3：输入四个点坐标，判断是凹四边形（false）还是凸四边形(true)，输出四边形周长、面积，结果之间以一个英文空格符分隔。若四个点坐标无法构成四边形，输出"not a quadrilateral"
4：输入六个点坐标，前两个点构成一条直线，后四个点构成一个四边形或三角形，输出直线与四边形（也可能是三角形）相交的交点数量。如果交点有两个，再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积（不换行）。若直线与四边形或三角形的一条边线重合，输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入，输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
\2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
5：输入五个点坐标，输出第一个是否在后四个点所构成的四边形（限定为凸四边形，不考虑凹四边形）或三角形（判定方法见选项4）的内部（若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。如果点在多边形的某条边上，输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形，输出"not a quadrilateral or triangle"。

思路分析:

图一：

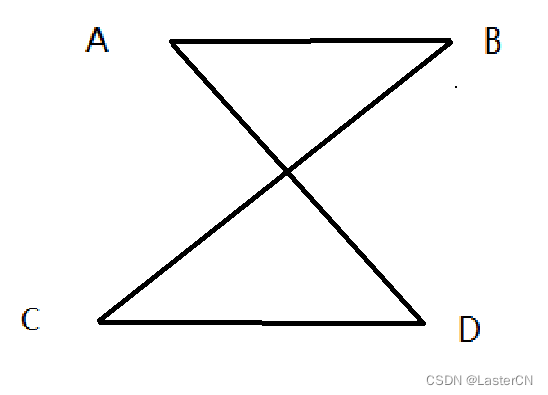
异常四边形

图二：凹四边形

凹四边形

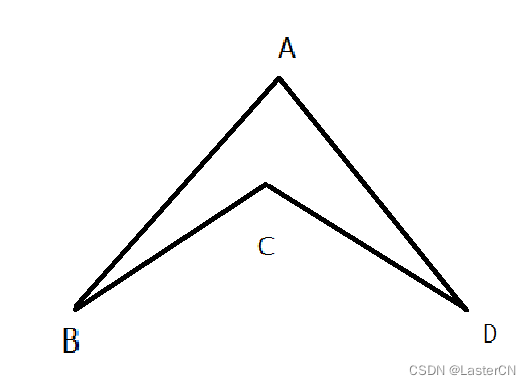
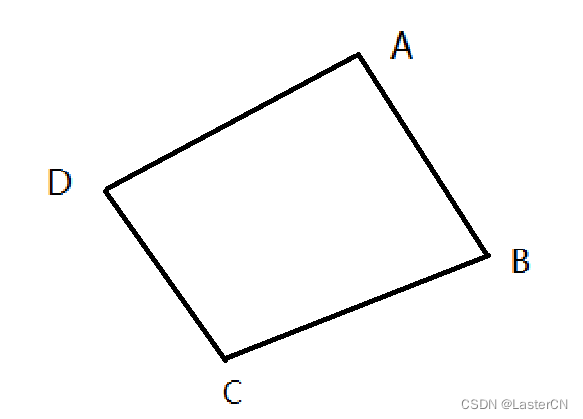
图三：凸四边形：

凸四边形

cmd == 1: 无法构成四边形的情况有三种：
1. 四个点有重合点 (无法构成边)
2. 有超过三点共线（可能构成三角形，反正不会是四边形）
3. 如图一异常四边形（任一对边 [线段] 有交点则异常）
cmd == 2:
1. 菱形：四边形四条边长度相等
2. 矩形：对角线长度相等
3. 正方形：菱形 + 矩形
cmd == 3:
1. 判断四边形是凸还是凹可根据四边形不同对角线分割出来的两三角形面积和是否相等判断，例如：
  
  在图二凹四边形中：△(ABC)+△(ADC) != △(ABD)+△(ACD);
  
  在图三凸三角形中：△(ABC)+△(ADC) == △(ABD)+△(ACD);
2. 周长：求和即可
3. 面积：自然会想到用对角线分割四边形为两个三角形再求和得到。但是！这样的方法只针对于凸四边形，看看上面1中的式子，凹四边形不同的对角线分割出来的两三角形面积和是不一样的，而四边形面积只和其中的较小者相同，对此用两条对角线分割求两次，取较小者即可。
cmd == 4:
1. 后者构成了四边形：
  和构成三角形求法几乎一模一样，只不过多了交点在两对角，交点在两对边的情况
  例如：
  直线交于图三中的AC两点；
  直线交于图三中的AB,CD两边
  直线交于图三中的BC,DA两边
2. 后者构成了三角形：
  直接copy上一次练习的代码就行 (练习3
cmd == 5:
图形是三角形还是四边形。见（cmd==4）
判断点P是否在图形之内，用面积法判断,（图形的任意相邻两点和P构成的三角形面积和是否等于图形面积）
例如在图三中有一个点P
判断 △(ABP) + △(BCP) + △(CDP) + △(DAP) 和 □(ABCD) 的面积是否相等。
相等则在三角形内部，不相等则在外部。
在内部也可能在边之上，特判即可。

code:[由于所依赖的类进行了重构，代码可能不起作用]

package nchu_software_oop_2022_4;

import java.util.*;
import Points.*;

public class p_2 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String str = sc.nextLine();

        //判断输入格式是否正确
        if(!str.matches("^[1-5][:](([+-]?(0|(0\\.\\d+)|[1-9][0-9]*(\\.\\d+)?))[,]([+-]?(0|(0\\.\\d+)|[1-9][0-9]*(\\.\\d+)?))\\s?)+$")){
            System.out.println("Wrong Format");
            System.exit(0);
        }

        //取出cmd，将串转化为浮点型
        int cmd = str.charAt(0)-'0';
        str = str.substring(2).trim();
        String[] tmpstr = str.split(" |,");
        double[] num = new double[30];
        int cnt = 0;
        for(String s:tmpstr){
            if(!check(s)){
                System.out.println("Wrong Format");
                System.exit(0);
            }
            num[cnt++] = Double.parseDouble(s);
        }

        //将浮点型转化为坐标点型
        Point[] p = new Point[10];
        for(int i=0;i<cnt;i+=2){
            p[i/2] = new Point(num[i],num[i+1]);
        }


        //点数不合法
        if(cmd==1 || cmd==2 || cmd==3){
            if(cnt != 8){
                System.out.println("wrong number of points");
                return;
            }
        }
        if(cmd==4){
            if(cnt != 12){
                System.out.println("wrong number of points");
                return;
            }
        }
        if(cmd == 5){
            if(cnt != 10){
                System.out.println("wrong number of points");
                return;
            }
        }


        if(cmd == 1){
            try{
                Quadrilateral q = new Quadrilateral(p[0],p[1],p[2],p[3]);
                System.out.printf("true %s\n",q.isParallelQuadrilateral());
            }catch (Exception e){
                if(e.getMessage().equals("not a quadrilateral"))
                    System.out.println("false false");
                else System.out.println(e.getMessage());
            }
        }
        if(cmd == 2){   //题目描述出问题！！
            try{
                Quadrilateral q = new Quadrilateral(p[0],p[1],p[2],p[3]);
                System.out.printf("%s %s %s\n",q.isDiamond(),q.isRectangle(),q.isSquare());
            }catch (Exception e){
                System.out.println("not a quadrilateral");
            }
        }
        if(cmd == 3){
            try{
                Quadrilateral q = new Quadrilateral(p[0],p[1],p[2],p[3]);
                System.out.printf("%s %s %s\n",q.isConvexQuadrilateral(),change(q.sideLength()), change(q.area()) );
            }catch (Exception e){
                System.out.println(e.getMessage());
            }
        }
        if(cmd == 4){
            Line l = null;
            Quadrilateral q = null;
            try{
                l = new Line(p[0],p[1]);
            }catch (Exception e){   //不构成直线
                System.out.println(e.getMessage());
                System.exit(0);
            }

            try{   //构成四边形(执行有关四边形的计算)
                q = new Quadrilateral(p[2],p[3],p[4],p[5]);
                solve(l,q);
                return;
            }catch (Exception e){   //可能构成三角形
                try{    //保证以下代码正确，捕获异常并吞并
                    //以5号点作为s顶点
                    if(!p[2].isSameTo(p[4])){   //2,4点不重合
                        Line ll = new Line(p[2],p[4]);
                        //3在ll之上，5在ll之外
                        if(p[3].inLineSegment_close(ll) && !p[5].inLineSegment_close(ll)){
                            Triangle t = new Triangle(p[2],p[4],p[5]);
                            solve(l,t);
                            return;
                        }
                    }
                    else{   //2,4点重合
                        if(!p[2].isSameTo(p[3])){   //但是2,3点不重合
                            Line ll = new Line(p[2],p[3]);
                            if(!p[5].inLineSegment_close(ll)){  //5点在ll线之外
                                Triangle t = new Triangle(p[2],p[3],p[5]);
                                solve(l,t);
                                return;
                            }
                        }
                    }
                    //以2号点作为顶点
                    if(!p[3].isSameTo(p[5])){
                        Line ll = new Line(p[3],p[5]);
                        if(p[4].inLineSegment_close(ll) && !p[2].inLine(ll)){
                            Triangle t = new Triangle(p[2],p[3],p[5]);
                            solve(l,t);
                            return;
                        }
                    }
                    else{
                        if(!p[3].isSameTo(p[4])){
                            Line ll = new Line(p[3],p[4]);
                            if(!p[2].inLineSegment_close(ll)){
                                Triangle t = new Triangle(p[2],p[3],p[4]);
                                solve(l,t);
                                return;
                            }
                        }
                    }
                    //以4号点作为顶点
                    if(!p[3].isSameTo(p[5])){
                        Line ll = new Line(p[3],p[5]);
                        if(p[2].inLineSegment_close(ll) && !p[4].inLine(ll)){
                            Triangle t = new Triangle(p[3],p[4],p[5]);
                            solve(l,t);
                            return;
                        }
                    }
                    //以3号点作为顶点
                    if(!p[2].isSameTo(p[4])){
                        Line ll = new Line(p[2],p[4]);
                        if(p[5].inLineSegment_close(ll) && !p[3].inLine(ll)){
                            Triangle t = new Triangle(p[2],p[3],p[4]);
                            solve(l,t);
                            return;
                        }
                    }



                    //不构成三角形
                    System.out.println("not a quadrilateral or triangle");


                }catch(Exception ee){}


            }

        }
        if(cmd == 5){
            try{    //四点构成四边形
                Quadrilateral q = new Quadrilateral(p[1],p[2],p[3],p[4]);
                int op = q.isContainPoint(p[0]);
                if(op == 0) System.out.println("in the quadrilateral");
                else if(op == 1) System.out.println("on the quadrilateral");
                else System.out.println("outof the quadrilateral");
            }catch(Exception e){    //不构成四边形，待确定是否构成三角形
                try{    //保证以下代码正确，捕获异常并吞并
                    //以4号点作为s顶点
                    if(!p[1].isSameTo(p[3])){   //1,3点不重合
                        Line ll = new Line(p[1],p[3]);
                        //2在ll之上，4在ll之外
                        if(p[2].inLineSegment_close(ll) && !p[4].inLineSegment_close(ll)){
                            Triangle t = new Triangle(p[1],p[3],p[4]);
                            inTriangle(p[0],t);
                            return;
                        }
                    }
                    else{   //1,3点重合
                        if(!p[1].isSameTo(p[2])){   //但是2,3点不重合
                            Line ll = new Line(p[1],p[2]);
                            if(!p[4].inLineSegment_close(ll)){  //5点在ll线之外
                                Triangle t = new Triangle(p[1],p[2],p[4]);
                                inTriangle(p[0],t);
                                return;
                            }
                        }
                    }
                    //以1号点作为顶点
                    if(!p[2].isSameTo(p[4])){
                        Line ll = new Line(p[2],p[4]);
                        if(p[3].inLineSegment_close(ll) && !p[1].inLine(ll)){
                            Triangle t = new Triangle(p[1],p[2],p[4]);
                            inTriangle(p[0],t);
                            return;
                        }
                    }
                    else{
                        if(!p[2].isSameTo(p[3])){
                            Line ll = new Line(p[2],p[3]);
                            if(!p[1].inLineSegment_close(ll)){
                                Triangle t = new Triangle(p[1],p[2],p[3]);
                                inTriangle(p[0],t);
                                return;
                            }
                        }
                    }
                    //以3号点作为顶点
                    if(!p[2].isSameTo(p[4])){
                        Line ll = new Line(p[2],p[4]);
                        if(p[1].inLineSegment_close(ll) && !p[3].inLine(ll)){
                            Triangle t = new Triangle(p[2],p[3],p[4]);
                            inTriangle(p[0],t);
                            return;
                        }
                    }
                    //以2号点作为顶点
                    if(!p[1].isSameTo(p[3])){
                        Line ll = new Line(p[1],p[3]);
                        if(p[4].inLineSegment_close(ll) && !p[2].inLine(ll)){
                            Triangle t = new Triangle(p[1],p[2],p[3]);
                            inTriangle(p[0],t);
                            return;
                        }
                    }

                    //不构成三角形
                    System.out.println("not a quadrilateral or triangle");


                }catch(Exception ee){}
            }

        }

    }



    public static boolean check(String str){
        return str.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$");
    }
    public static void pr_ans(Triangle t, Point a,Point b,Point c){
        double[] ans = new double[2];
        ans[0] = Triangle.area(a,b,c);
        ans[1] = t.area() - ans[0];
        Arrays.sort(ans);
        System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
    }
    public static void pr_ans(Quadrilateral q,Point a,Point b,Point c){
        double[] ans = new double[2];
        ans[0] = Triangle.area(a,b,c);
        ans[1] = q.area() - ans[0];
        Arrays.sort(ans);
        System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
    }
    public static String change(double a){
        String res = String.format("%.3f",a);
        res = res.replaceAll("0+?$", "");
        if(res.charAt(res.length()-1) == '.') res+='0';
        return res;
    }


    //三角形交点情况，上次练习题copy
    public static void solve(Line l,Triangle t){
            //与任意一条边重合
            if(l.isSameTo(t.ab) || l.isSameTo(t.ac) || l.isSameTo(t.bc)){
                System.out.println("The line is coincide with one of the lines");
                return;
            }
            //与三条边的交点(值可能为null,即平行)
            Point p_ab = l.getIntersection(t.ab);
            Point p_ac = l.getIntersection(t.ac);
            Point p_bc = l.getIntersection(t.bc);


            //三交点是否位于边之内
            boolean p_ab_in=false, p_ac_in =false, p_bc_in=false;
            if(p_ab != null)  p_ab_in = p_ab.inLineSegment(t.ab);
            if(p_ac != null)  p_ac_in = p_ac.inLineSegment(t.ac);
            if(p_bc != null)  p_bc_in = p_bc.inLineSegment(t.bc);


            //任一角在直线之上(特判三角形的角)
            if(t.a.inLine(l)){
                //与另一条边无交点或者交点在边之外
                if(p_bc == null || !p_bc.inLineSegment_close(t.bc)){
                    System.out.println("1");
                }
                else pr_ans(t,t.a,t.b,p_bc);
                return;
            }
            if(t.b.inLine(l)){
                if(p_ac == null || !p_ac.inLineSegment_close(t.ac)){
                    System.out.println("1");
                }
                else pr_ans(t,t.a,t.b,p_ac);
                return;
            }
            if(t.c.inLine(l)){
                if(p_ab == null || !p_ab.inLineSegment_close(t.ab)){
                    System.out.println("1");
                }
                else pr_ans(t,t.a,t.c,p_ab);
                return;
            }

            //两个交点
            if(p_ab_in && p_bc_in){ pr_ans(t,t.b,p_ab,p_bc);return;}
            if(p_ab_in && p_ac_in){ pr_ans(t,t.a,p_ab,p_ac);return;}
            if(p_bc_in && p_ac_in){ pr_ans(t,t.c,p_bc,p_ac);return;}
            //无交点
            System.out.println("0");

    }

    //四边形交点情况
    public static void solve(Line l,Quadrilateral q){
        //与任意一条边重合
        for(Line ll: q.lines){
            if(l.isSameTo(ll)){
                System.out.println("The line is coincide with one of the lines");
                return;
            }
        }

        //与四条边的交点，可能为null;
        Point p0 = l.getIntersection(q.lines[0]);
        Point p1 = l.getIntersection(q.lines[1]);
        Point p2 = l.getIntersection(q.lines[2]);
        Point p3 = l.getIntersection(q.lines[3]);

        //判断交点是否在边之上
        boolean p0_in = false,p1_in = false,p2_in = false,p3_in = false;
        if(p0 != null) p0_in = p0.inLineSegment(q.lines[0]);
        if(p1 != null) p1_in = p1.inLineSegment(q.lines[1]);
        if(p2 != null) p2_in = p2.inLineSegment(q.lines[2]);
        if(p3 != null) p3_in = p3.inLineSegment(q.lines[3]);

        //任一角在直线l之上
        if(q.points[0].inLine(l)){
            //它的对角也在边之上
            if(q.points[2].inLine(l)){
                pr_ans(q,q.points[0],q.points[1],q.points[2]);
            }
            //对角的邻边任一与直线有交点
            else if (p2_in){    //邻边之一
                pr_ans(q,q.points[0],p2,q.points[3]);
            }
            else if (p1_in){    //邻边之二
                pr_ans(q,q.points[0],p1,q.points[1]);
            }
            else{
                System.out.println("1");
            }
            return;
        }
        else if(q.points[1].inLine(l)){
            //它的对角也在边之上
            if(q.points[3].inLine(l)){
                pr_ans(q,q.points[1],q.points[2],q.points[3]);
            }
            //对角的邻边任一与直线有交点
            else if (p2_in){    //邻边之一
                pr_ans(q,q.points[1],p2,q.points[2]);
            }
            else if (p3_in){    //邻边之二
                pr_ans(q,q.points[1],p3,q.points[0]);
            }
            else{
                System.out.println("1");
            }
            return;
        }
        else if (q.points[2].inLine(l)) {
            //它的对角也在边之上
            if(q.points[0].inLine(l)){
                pr_ans(q,q.points[2],q.points[3],q.points[0]);
            }
            //对角的邻边任一与直线有交点
            else if (p3_in){    //邻边之一
                pr_ans(q,q.points[2],p3,q.points[3]);
            }
            else if (p0_in){    //邻边之二
                pr_ans(q,q.points[2],p0,q.points[1]);
            }
            else{
                System.out.println("1");
            }
            return;
        }
        else if (q.points[3].inLine(l)) {
            //它的对角也在边之上
            if(q.points[1].inLine(l)){
                pr_ans(q,q.points[3],q.points[0],q.points[1]);
            }
            //对角的邻边任一与直线有交点
            else if (p0_in){    //邻边之一
                pr_ans(q,q.points[3],p0,q.points[0]);
            }
            else if (p1_in){    //邻边之二
                pr_ans(q,q.points[3],p1,q.points[2]);
            }
            else{
                System.out.println("1");
            }
            return;
        }

        //两个交点(邻边)
        if(p0_in && p1_in){pr_ans(q,p0,p1,q.points[1]);return;}
        if(p1_in && p2_in){pr_ans(q,p1,p2,q.points[2]);return;}
        if(p2_in && p3_in){pr_ans(q,p2,p3,q.points[3]);return;}
        if(p3_in && p0_in){pr_ans(q,p3,p0,q.points[0]);return;}
        //对边
        if(p0_in && p2_in){
            double[] ans = new double[2];
            ans[0] = Triangle.area(q.points[0],p0,p2) + Triangle.area(p0,p2,q.points[3]);
            ans[1] = Triangle.area(q.points[1],p0,p2) + Triangle.area(p0,p2,q.points[2]);
            Arrays.sort(ans);
            System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
            return;
        }
        if(p1_in && p3_in){
            double[] ans = new double[2];
            ans[0] = Triangle.area(q.points[1],p1,p3) + Triangle.area(p1,p3,q.points[0]);
            ans[1] = Triangle.area(q.points[2],p1,p3) + Triangle.area(p1,p3,q.points[3]);
            Arrays.sort(ans);
            System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
            return;
        }
        //0交点
        System.out.println("0");

    }


    //判断点在三角形哪里
    public static void inTriangle(Point p,Triangle t){
        int op = t.isContainPoint(p);
        if(op == 0) System.out.println("in the triangle");
        else if (op == 1) System.out.println("on the triangle");
        else System.out.println("outof the triangle");
    }
}

3.2 点线形系列5-凸五边形的计算

题目描述:[两次作业一起]

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入五个点坐标，判断是否是五边形，判断结果输出true/false。
2：输入五个点坐标，判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，结果之间以一个英文空格符分隔。若五个点坐标无法构成五边形，输出"not a pentagon"
3：输入七个点坐标，前两个点构成一条直线，后五个点构成一个凸五边形、凸四边形或凸三角形，输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个，再按面积从小到大输出被直线分割成两部分的面积（不换行）。若直线与多边形形的一条边线重合，输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入，若前两点重合，输出"points coincide"。

4：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），判断它们两个之间是否存在包含关系（一个多边形有一条或多条边与另一个多边形重合，其他部分都包含在另一个多边形内部，也算包含）。
两者存在六种关系：1、分离（完全无重合点） 2、连接（只有一个点或一条边重合） 3、完全重合 4、被包含（前一个多边形在后一个多边形的内部）5、交错 6、包含（后一个多边形在前一个多边形的内部）。
各种关系的输出格式如下：
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon

5：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），输出两个多边形公共区域的面积。注：只考虑每个多边形被另一个多边形分割成最多两个部分的情况，不考虑一个多边形将另一个分割成超过两个区域的情况。
6：输入六个点坐标，输出第一个是否在后五个点所构成的多边形（限定为凸多边形，不考虑凹多边形），的内部（若是五边形输出in the pentagon/outof the pentagon，若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。输入入错存在冗余点要排除，冗余点的判定方法见选项5。如果点在多边形的某条边上，输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
\2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

思路分析:

cmd == 1
使用Graphical构造实例，直接判断实例属性[ len ] 是否等于5即可
cmd ==2
同上，判断[ isConvexGraphical ] 是否为真即可，为真则输出[ sidelength ] [ area ]
cmd == 3
同上构造出实例，判断[ len ] 的值，等于3构造Triangle实例等于4则构造Quadrilateral实例，等于5则构造Pentagon实例。
前两者上次作业都有，如果是构造了五边形
1. 特判line与边重合
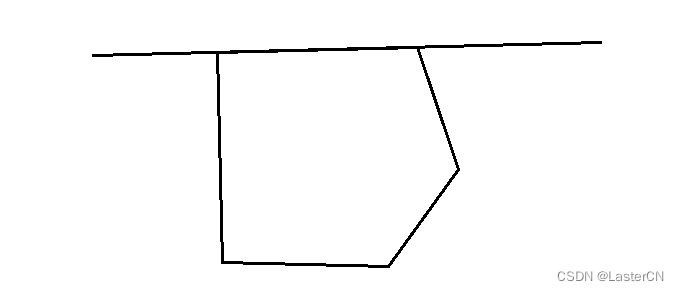
2. 特判某点在line上面的情况，分别有：
  
  只交这个点，
  
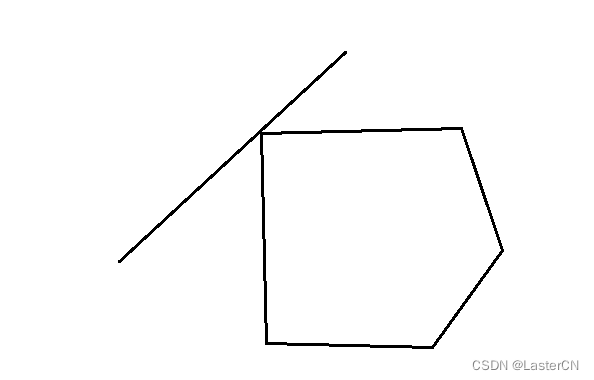
  和对角任一角相交，
  
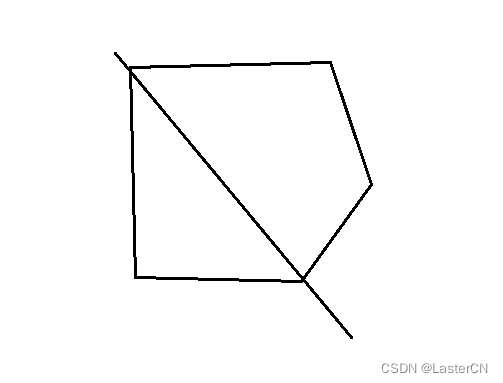
  和两个对边邻边（任一）相交，
  
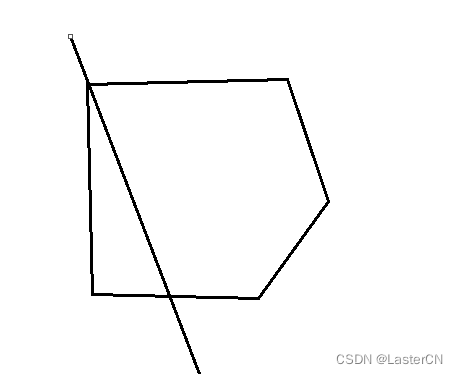
  和对边相交
3. 任意相交与两个边
cmd == 4
实例化两个Graphical对象，如果[ status ] 为-1则输出异常信息
调用relationshipWith函数
cmd == 5
实例化同上
调用overlappingArea函数
cmd == 6
实例化一个Graphical对象
调用isContainPoint函数

code:

package nchu_software_oop_2022_5;

import java.util.*;

import Points.*;

public class p_1 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String str = sc.nextLine();

        //判断输入格式是否正确
        if(!str.matches("^[1-5][:](([+-]?(0|(0\\.\\d+)|[1-9][0-9]*(\\.\\d+)?))[,]([+-]?(0|(0\\.\\d+)|[1-9][0-9]*(\\.\\d+)?))\\s?)+$")){
            System.out.println("Wrong Format");
            System.exit(0);
        }

        //取出cmd，将串转化为浮点型
        int cmd = str.charAt(0)-'0';
        str = str.substring(2).trim();
        String[] tmpstr = str.split(" |,");
        double[] num = new double[30];
        int cnt = 0;
        for(String s:tmpstr){
            if(!check(s)){
                System.out.println("Wrong Format");
                System.exit(0);
            }
            num[cnt++] = Double.parseDouble(s);
        }

        //将浮点型转化为坐标点型
        Point[] p = new Point[10];
        for(int i=0;i<cnt;i+=2){
            p[i/2] = new Point(num[i],num[i+1]);
        }

        pointsCntCheck(cmd,cnt);

        if(cmd == 1){
            try{
                Pentagon pentagon = new Pentagon(new Point[]{p[0],p[1],p[2],p[3],p[4]});
                System.out.println("true");
            }catch (Exception reason){
                System.out.println("false");
            }
        }
        else if(cmd == 2){
            try{
                Pentagon pentagon = new Pentagon(new Point[]{p[0],p[1],p[2],p[3],p[4]});
                if(pentagon.isConvexGraphical){
                    System.out.printf("%s %s %s\n",pentagon.isConvexGraphical,change(pentagon.sideLength),change(pentagon.area));
                }
                else System.out.println("false");
            }catch (Exception reason){
                System.out.println(reason.getMessage());
            }
        }
        else if(cmd == 3){
            Line line = null;
            try{
                line = new Line(p[0],p[1]);
            }
            catch (Exception reason){
                System.out.println(reason.getMessage());
            }

            Graphical graphical = new Graphical(new Point[]{p[2],p[3],p[4],p[5],p[6]});
            if(graphical.status == -1){
                System.out.println("not a polygon");
                System.exit(0);
            }
            if(graphical.len == 5){
                try{
                    Pentagon pentagon = new Pentagon(graphical.points);
                    solve(line,pentagon);

                }catch (Exception reason){}
            }
            if(graphical.len == 4){
                try{

                    Quadrilateral quadrilateral = new Quadrilateral(graphical.points);
                    solve(line,quadrilateral);

                }catch (Exception reason){}
            }
            if(graphical.len == 3){
                try{
                    Triangle triangle = new Triangle(graphical.points);
                    solve(line,triangle);

                }catch (Exception reason){}

            }
        }





        /*main end*/
    }

    public static void solve(Line line,Pentagon pentagon){
        for(Line item:pentagon.lines){
            if(line.isSameTo(item)){
                System.out.println("The line is coincide with one of the lines");
                return;
            }
        }
        Point[] intersections = new Point[5];
        for(int i=0;i<5;i++){
            intersections[i] = line.getIntersection(pentagon.lines[i]);
        }
        boolean[] check = new boolean[]{false,false,false,false,false};
        for(int i=0;i<5;i++){
            if(intersections[i] != null){
                check[i] = intersections[i].inLineSegment(pentagon.lines[i]);
            }
        }
        //以上求出交点，并求出交点是否在边之上

        /*特判交点在角上面的情况*/
        for(int i=0;i<5;i++){
            if(pentagon.points[i].inLine(line)){
                //两个不相邻角在line之上
                if(pentagon.points[(i+2)%pentagon.len].inLine(line)){
                    pr_ans(pentagon,pentagon.points[i], pentagon.points[(i+1)%pentagon.len], pentagon.points[(i+2)%pentagon.len]);
                }
                else if(pentagon.points[(i+3)%pentagon.len].inLine(line)){
                    pr_ans(pentagon,pentagon.points[i], pentagon.points[(i+3)%pentagon.len], pentagon.points[(i+4)%pentagon.len]);
                }
                //对边和line有交点(分割为两个四边形)
                else if(check[(i+2)%pentagon.len]){
                    Graphical tmp = new Graphical(new Point[]{pentagon.points[i], pentagon.points[(i+1)%pentagon.len], pentagon.points[(i+2)%pentagon.len], intersections[(i+2)%pentagon.len]});
                    double[] ans = new double[]{tmp.area, pentagon.area - tmp.area};
                    Arrays.sort(ans);
                    System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
                }
                //剩余两个不相邻边和line有交点
                else if(check[(i+1)%pentagon.len]){
                    pr_ans(pentagon,pentagon.points[i], pentagon.points[(i+1)%pentagon.len], intersections[(i+1)%pentagon.len]);
                }
                else if(check[(i+3)%pentagon.len]){
                    pr_ans(pentagon,pentagon.points[i], pentagon.points[(i+4)%pentagon.len], intersections[(i+3)%pentagon.len]);
                }
                //就一个交点
                else{
                    System.out.println("1");
                }

                return;//别忘了
            }
        }

        /*交点分别在边上面的情况*/
        for(int i=0;i<5;i++){
            if(check[i] && check[(i+2)%pentagon.len]){
                Graphical tmp = new Graphical(new Point[]{intersections[i], pentagon.points[(i+1)%pentagon.len], pentagon.points[(i+2)%pentagon.len], intersections[(i+2)%pentagon.len]});
                double[] ans = new double[]{tmp.area, pentagon.area - tmp.area};
                Arrays.sort(ans);
                System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
                return;
            }
            if(check[i] && check[(i+3)%pentagon.len]){
                Graphical tmp = new Graphical(new Point[]{intersections[i], pentagon.points[i], pentagon.points[(i+4)%pentagon.len], intersections[(i+3)%pentagon.len]});
                double[] ans = new double[]{tmp.area, pentagon.area - tmp.area};
                Arrays.sort(ans);
                System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
                return;
            }
        }

        /*无交点*/
        System.out.println("0");

    }
    public static void solve(Line line,Quadrilateral q){
    //与任意一条边重合
        for(Line item: q.lines){
            if(line.isSameTo(item)){
                System.out.println("The line is coincide with one of the lines");
                return;
            }
        }

        Point[] intersections = new Point[4];
        for(int i=0;i<4;i++){
            intersections[i] = line.getIntersection(q.lines[i]);
        }
        boolean[] check = new boolean[]{false,false,false,false};
        for(int i=0;i<4;i++){
            if(intersections[i] != null){
                check[i] = intersections[i].inLineSegment(q.lines[i]);
            }
        }
        //以上求出交点，并求出交点是否在边之上

        /*特判交点在角上面的情况*/
        for(int i=0;i<4;i++){
            if(q.points[i].inLine(line)){
                //对角在line之上
                if(q.points[(i+2)%q.len].inLine(line)){
                    pr_ans(q,q.points[i], q.points[(i+1)%q.len], q.points[(i+2)%q.len]);
                }
                //两个对边和line有交点
                else if(check[(i+1)%q.len]){
                    pr_ans(q, q.points[i], q.points[(i+1)%q.len], intersections[(i+1)%q.len]);
                }
                else if(check[(i+2)%q.len]){
                    pr_ans(q, q.points[i], q.points[(i+3)%q.len], intersections[(i+2)%q.len]);
                }
                //就一个交点
                else{
                    System.out.println("1");
                }

                return;//别忘了
            }
        }

        /*两组对边和line有交点的情况*/
        for(int i=0;i<2;i++){
            if(check[i] && check[(i+2)%q.len]){
                Graphical tmp = new Graphical(new Point[]{intersections[i], q.points[(i+1)%q.len], q.points[(i+2)%q.len], intersections[(i+2)%q.len]});
                double[] ans = new double[]{tmp.area, q.area - tmp.area};
                Arrays.sort(ans);
                System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
                return;
            }
        }

        /*无交点*/
        System.out.println("0");
    }
    public static void solve(Line line,Triangle triangle){
        //与任意一条边重合
        if(line.isSameTo(triangle.lines[0]) || line.isSameTo(triangle.lines[1]) || line.isSameTo(triangle.lines[2])){
            System.out.println("The line is coincide with one of the lines");
            return;
        }
        //与三条边的交点(值可能为null,即平行)
        Point p_ab = line.getIntersection(triangle.lines[0]);
        Point p_bc = line.getIntersection(triangle.lines[1]);
        Point p_ca = line.getIntersection(triangle.lines[2]);


        //三交点是否位于边之内
        boolean p_ab_in=false, p_bc_in =false, p_ca_in=false;
        if(p_ab != null)  p_ab_in = p_ab.inLineSegment(triangle.lines[0]);
        if(p_bc != null)  p_bc_in = p_bc.inLineSegment(triangle.lines[1]);
        if(p_ca != null)  p_ca_in = p_ca.inLineSegment(triangle.lines[2]);


        //任一角在直线之上(特判三角形的角)
        if(triangle.points[0].inLine(line)){
            //与另一条边无交点或者交点在边之外
            if(p_ca == null || !p_ca.inLineSegment_close(triangle.lines[2])){
                System.out.println("1");
            }
            else pr_ans(triangle,triangle.points[0],triangle.points[1],p_ca);
            return;
        }
        if(triangle.points[1].inLine(line)){
            if(p_ca == null || !p_ca.inLineSegment_close(triangle.lines[1])){
                System.out.println("1");
            }
            else pr_ans(triangle,triangle.points[0],triangle.points[1],p_ca);
            return;
        }
        if(triangle.points[2].inLine(line)){
            if(p_ab == null || !p_ab.inLineSegment_close(triangle.lines[0])){
                System.out.println("1");
            }
            else pr_ans(triangle,triangle.points[0],triangle.points[2],p_ab);
            return;
        }

        //两个交点
        if(p_ab_in && p_bc_in){ pr_ans(triangle,triangle.points[1],p_ab,p_bc);return;}
        if(p_bc_in && p_ca_in){ pr_ans(triangle,triangle.points[2],p_bc,p_ca);return;}
        if(p_ca_in && p_ab_in){ pr_ans(triangle,triangle.points[0],p_ca,p_ab);return;}
        //无交点
        System.out.println("0");
    }
    public static void pr_ans(Triangle t, Point a,Point b,Point c){
        double[] ans = new double[2];
        ans[0] = Triangle.area(a,b,c);
        ans[1] = t.area - ans[0];
        Arrays.sort(ans);
        System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
    }
    public static void pr_ans(Quadrilateral q,Point a,Point b,Point c){
        double[] ans = new double[2];
        ans[0] = Triangle.area(a,b,c);
        ans[1] = q.area - ans[0];
        Arrays.sort(ans);
        System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
    }
    public static void pr_ans(Pentagon pentagon,Point a,Point b,Point c){
        double[] ans = new double[2];
        ans[0] = Triangle.area(a,b,c);
        ans[1] = pentagon.area - ans[0];
        Arrays.sort(ans);
        System.out.printf("2 %s %s\n",change(ans[0]),change(ans[1]));
    }
    public static void pointsCntCheck(int cmd,int cnt){
        if(cmd == 1 || cmd == 2){
            if(cnt != 10){
                System.out.println("wrong number of points");
                System.exit(0);
            }
        }
        if(cmd == 3){
            if(cnt != 14){
                System.out.println("wrong number of points");
                System.exit(0);
            }
        }
    }
    public static boolean check(String str){
        return str.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$");
    }
    public static String change(double a){
        String res = String.format("%.3f",a);
        res = res.replaceAll("0+?$", "");
        if(res.charAt(res.length()-1) == '.') res+='0';
        return res;
    }


}

package nchu_software_oop_2022_5;
import Points.*;

import java.util.Scanner;

public class p_2 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String str = sc.nextLine();

        //判断输入格式是否正确
        if(!str.matches("^[1-9][:](([+-]?(0|(0\\.\\d+)|[1-9][0-9]*(\\.\\d+)?))[,]([+-]?(0|(0\\.\\d+)|[1-9][0-9]*(\\.\\d+)?))\\s?)+$")){
            System.out.println("Wrong Format");
            System.exit(0);
        }

        //取出cmd，将串转化为浮点型
        int cmd = str.charAt(0)-'0';
        str = str.substring(2).trim();
        String[] tmpstr = str.split(" |,");
        double[] num = new double[30];
        int cnt = 0;
        for(String s:tmpstr){
            if(!check(s)){
                System.out.println("Wrong Format");
                System.exit(0);
            }
            num[cnt++] = Double.parseDouble(s);
        }

        //将浮点型转化为坐标点型
        Point[] p = new Point[10];
        for(int i=0;i<cnt;i+=2){
            p[i/2] = new Point(num[i],num[i+1]);
        }

        pointsCntCheck(cmd,cnt);

        if(cmd == 4){
            Graphical graphical1 = new Graphical(new Point[]{p[0], p[1], p[2], p[3], p[4]});
            Graphical graphical2 = new Graphical(new Point[]{p[5], p[6], p[7], p[8], p[9]});
            System.out.println(graphical1.relationshipWith(graphical2));
        }
        if(cmd == 5){
            Graphical graphical1 = new Graphical(new Point[]{p[0], p[1], p[2], p[3], p[4]});
            Graphical graphical2 = new Graphical(new Point[]{p[5], p[6], p[7], p[8], p[9]});
            System.out.println(change(graphical1.overlappingArea(graphical2)));
//            graphical1.print();
//            graphical2.print();
        }
        if(cmd == 6){
            Graphical graphical1 = new Graphical(new Point[]{p[1], p[2], p[3], p[4], p[5]});
            int res = graphical1.isContainPoint(p[0]);
            String[] name = new String[]{"triangle", "quadrilateral", "pentagon"};
            if(res == -1){
                System.out.println("in the "+name[graphical1.len-3]);
            }
            if(res == 0){
                System.out.println("on the "+name[graphical1.len-3]);
            }
            if(res == 1){
                System.out.println("outof the "+name[graphical1.len-3]);
            }
        }

    }
    public static void pointsCntCheck(int cmd,int cnt){
        if(cmd == 4 || cmd == 5){
            if(cnt != 20){
                System.out.println("wrong number of points");
                System.exit(0);
            }
        }
        if(cmd == 6){
            if(cnt != 12){
                System.out.println("wrong number of points");
                System.exit(0);
            }
        }
    }

    public static String change(double a){
        String res = String.format("%.3f",a);
        res = res.replaceAll("0+?$", "");
        if(res.charAt(res.length()-1) == '.') res+='0';
        return res;
    }

    public static boolean check(String str){
        return str.matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$");
    }
}

3.3 期中考试

第一题只需封装好Point,Line类两者即可，且当中只涉及计算两点距离
第二题在第一题的基础上，加入了Plane类，并抽离出了Element类作为前三者的抽象类
第三题在第二题的基础上，加入了GeometryObject容器类，用于存放Element

Point extends Element:

属性：x,y

方法：对x,y的get 和 set ，disToPoint(点到点的距离) , display

Line extends Element:

属性：point1 , point2 , color

方法：对属性的get 和 set getDistance(point1和point2的距离) , display

Plane extends Element:

属性：color

方法：对属性的get 和 set display

Element:

方法：display

GeometryObject:

属性：list

方法：getList , add(向list添加元素) , remove(移除链表末尾元素)

对应类图：

类code:

Point extends Element:

public class Point extends Element{
    private double x = 0;
    private double y = 0;
    public Point(){}
    public Point(double x,double y){
        this.x = x;
        this.y = y;
    }


    public double disToPoint(Point another){
        return Math.sqrt(Math.pow(this.x-another.x,2) + Math.pow(this.y-another.y,2));
    }
    public void display(){
        System.out.printf("(%.2f,%.2f)\n",this.x,this.y);
    }

    public double getX() {
        return x;
    };

    public void setX(double x) {
        this.x = x;
    }

    public double getY() {
        return y;
    }

    public void setY(double y) {
        this.y = y;
    }

}

Line extends Element:

public class Line extends Element{
    private Point point1,point2;
    private String color;
    public Line(Point a, Point b, String color){
        this.point1 = a;
        this.point2 = b;
        this.color = color;
    }


    public double getDistance(){
        return this.point1.disToPoint(this.point2);
    }

    public void display(){
        System.out.printf("The line's color is:%s\n",this.color);
        System.out.println("The line's begin point's Coordinate is:");
        this.point1.display();
        System.out.println("The line's end point's Coordinate is:");
        this.point2.display();
        System.out.printf("The line's length is:%.2f\n",this.getDistance());
    }

    public Point getPoint1() {
        return point1;
    }

    public Point getPoint2() {
        return point2;
    }

    public String getColor() {
        return color;
    }

    public void setColor(String color) {
        this.color = color;
    }

    public void setPoint1(Point point1) {
        this.point1 = point1;
    }

    public void setPoint2(Point point2) {
        this.point2 = point2;
    }
}

Plane extends Element:

public class Plane extends Element{
    private String color;

    public Plane(){}
    public  Plane(String color){
        this.color = color;
    }
    @Override
    public void display() {
        System.out.printf("The Plane's color is:%s\n",this.color);
    }


    public String getColor() {
        return color;
    }

    public void setColor(String color) {
        this.color = color;
    }
}

Element:

public abstract class Element {
    public abstract void display();
}

GeometryObject:

import java.util.ArrayList;

public class GeometryObject {
    private ArrayList<Element> list = new ArrayList<>();

    public GeometryObject(){}


    public void add(Element element){
        this.list.add(element);
    }

    public void remove(int index){
        try {
            this.list.remove(index);
        }catch (Exception reason){}

    }

    public ArrayList<Element> getList() {
        return list;
    }
}

实现code:

code1:

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String str;

        Point[] points = new Point[2];
        Line line;

        for(int i=0;i<2;i++){
            double x,y;
            x = sc.nextDouble();
            y = sc.nextDouble();
            check(x);
            check(y);
            points[i] = new Point(x,y);
        }
        str = sc.next();
        line = new Line(points[0],points[1],str);
        line.display();

    }
    public static void check(double x){
        if(x <= 0 || x > 200){
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }
}

code2:

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String str;

        Point[] points = new Point[2];
        Line line;

        for(int i=0;i<2;i++){
            double x,y;
            x = sc.nextDouble();
            y = sc.nextDouble();
            check(x);
            check(y);
            points[i] = new Point(x,y);
        }
        str = sc.next();
        line = new Line(points[0],points[1],str);
        Plane plane = new Plane(str);
        Point a = line.getPoint1();
        Point b = line.getPoint2();


        a.display();
        b.display();
        line.display();
        plane.display();

    }
    public static void check(double x){
        if(x <= 0 || x > 200){
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }

}

code3:

import java.util.*;
import java.util.ArrayList;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        GeometryObject geometryObject = new GeometryObject();
        double x,y;
        String str;

        int cmd;
        while (true){
            cmd = sc.nextInt();
            switch (cmd){
                case 1:{
                    Point point;
                    x = sc.nextDouble();
                    check(x);
                    y = sc.nextDouble();
                    check(y);
                    point = new Point(x,y);
                    geometryObject.add(point);
                    break;
                }
                case 2:{
                    Point[] points = new Point[2];
                    for(int i=0;i<2;i++){
                        x = sc.nextDouble();
                        check(x);
                        y = sc.nextDouble();
                        check(y);
                        points[i] = new Point(x,y);

                    }
                    str = sc.next();
                    Line line = new Line(points[0], points[1],str);
                    geometryObject.add(line);
                    break;
                }
                case 3:{
                    str = sc.next();
                    Plane plane = new Plane(str);
                    geometryObject.add(plane);
                    break;
                }
                case 4:{
                    int index = sc.nextInt();
                    geometryObject.remove(index-1);
                    break;
                }
                default:{
                    ArrayList<Element> list = geometryObject.getList();
                    for (Element item : list){
                        item.display();
                    }
                    System.exit(0);
                }
            }
        }

    }
    public static void check(double x){
        if(x <= 0 || x > 200){
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }

}

4.踩坑心得

考试时pta的测试点文本对比...输出Wrong Format时多加了换行符格式错误，有点莫名其妙？
Scanner的nextline会保存换行符，类似于c里面的getchar,需要注意

5.改进建议

对于多个点构成的三角形，就拿四边形来说吧，我也是做完五边形之后才明白老师描述的合法三角形是指啥，明明只需要说明去除重合的点之后，剩下的点按照顺序首尾连接下去可以构成三角形则合法，老师描述的也太...抽象了, 这一块真的建议改进！！！
在点线系列四边形中，第二个选项，无论是点重合还是怎么样，都是输出"not a quadrilateral"，不会输出"points coincide"，属于是题目的描述出了问题，希望能改回去。

6.总结

这个系列到后面涉及了好多计算几何的算法，比如求任意多边形的面积，求任意图形的凹凸性，在最后一次求重叠面积时，可以求出两个图形的所有交点，然后对点集排序，最后构成新的图形求面积。虽然这些都过度完成了任务，但真可以去加强一下题目，并且给出对应的算法资料了解一下算法？
我封装的所有类的属性都是public可以从外界直接访问并修改的，安全性太差
Line这个类..我作为了直线，线段，向量一起使用，不太符合类单一功能的规则，有需要再拆分出来吧

标签：总结,系列,Point,double,another,return,Line,public
From： https://www.cnblogs.com/LasterCN/p/16837403.html

点线系列总结

1.前言

2.类

2.1 Point

2.2 Line

2.3 Graphical

2.4 Quadrilateral

2.5 Pentagon

3.设计与分析

3.1 点线形系列4-凸四边形的计算

3.2 点线形系列5-凸五边形的计算

3.3 期中考试

4.踩坑心得

5.改进建议

6.总结

相关文章

赞助商

阅读排行