大脑宕机低级大错误合集
- ceil 的精度问题:
int a, b;
ceil(a/b);//错误的
ceil(1.0*a/b);//正确的
- memset 的顺序:
memset(vis, 0, sizeof(vis);
后两项打反时编译器不会报错。
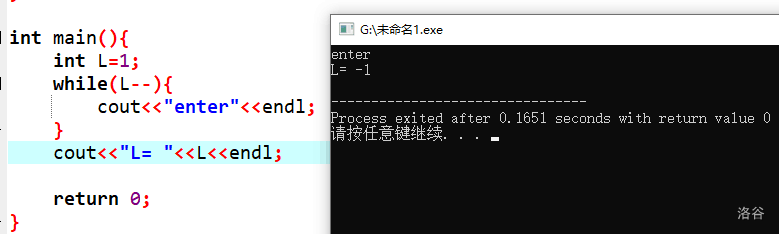
while(L--)判否后仍然会执行一次L--:
-
lower_bound 正确使用:
2 -
邻接矩阵遍历图时,严格注意强制类型转换!
for(int i=0; i < (int) ve[u].size(); i++){
int v=ve[u][i];
if(v == fa) continue;
dfs(v,u);
size[u]+= size[v];
f[u] = max(f[u], size[v]);
}
-
P6492 [COCI2010-2011#6] STEP
线段树维护区间最大连续字符相异长度,附单点修改。
错因: 左右子树下标移位
错解:
int ls= u<<2;
int rs =u<<2|1;
正解:
int ls= u<<1 ;
int rs= u<<1|1 ;
double 下的二分(二分实现某点导数间接实现三分)时,两个 double check() 直接进行比较即可,不用思考什么差值 eps ,eps 只是用于两个 double 判断是否相等,例如 if( fabs(x-y) <= eps ) 。
正解:
if(judge(mid+eps,nowansb) <= judge(mid-eps,nowansb) ) le=mid;
else rt=mid;
错解:
if(judge(mid+eps,__b) - judge(mid-eps,__b) <= eps ) le=mid;
else rt=mid;
如果数组开小了爆栈也可能 RE
正解
const int maxn=5e5+5;
错解
const int maxn=500000;
线段树维护区间最大最小值,如果outofrange() 为 true ,应该返回 INF 或 -INF,而非 0 。
正解:
ll qjcx(int u,int l,int r,int L,int R){
if(inrange(l,r,L,R))
return w[u];
else if(outofrange(l,r,L,R))return -INF;
else {
int mid=(l+r)>>1;
pushdown(u,l,r);
return max( qjcx(u*2,l,mid,L,R) , qjcx(u*2+1,mid+1,r,L,R) );
}
}
错解:
ll qjcx(int u,int l,int r,int L,int R){
if(inrange(l,r,L,R))
return w[u];
else if(outofrange(l,r,L,R))return 0;
else {
int mid=(l+r)>>1;
pushdown(u,l,r);
return max( qjcx(u*2,l,mid,L,R) , qjcx(u*2+1,mid+1,r,L,R) );
}
}
维护单点异或,区间查询。注意有 lzy[u] 才进行 maketag(u,len,lzy[u]) ,如果 lzy[u] 不存在时进行了异或操作标记下传,会导致错误的单点异或,因为他把 lzy[u] == 0 的异或下传了。
正解:
void pushdown(int u,int l,int r){
int mid=(l+r)>>1;
if(!lzy[u]) return ;
maketag(u*2,mid-l+1,lzy[u]);
maketag(u*2+1,r-mid,lzy[u]);
lzy[u]=0;
}
错解:
void pushdown(int u,int l,int r){
int mid=(l+r)>>1;
maketag(u*2,mid-l+1,lzy[u]);
maketag(u*2+1,r-mid,lzy[u]);
lzy[u]=0;
}
oier作死技巧
1.赋值运算符与判等不分
/使用-Wall编译选项会出现警告
if(n=1)puts("Yes");//此处应为n==1
else puts("No");
2.多重循环中i,j,k使用分布不清
for(int i=1;i<=n;i++)
for(int j=1;j<=n;i++)//显然应该是j++
//do something
for(int i=1;i<=n;i++)
for(int j=n;j>=1;j++)//显然应该是j--
//do something
3.运算符优先级(多用括号)
int a=num<<2+1;//这里会被解读为num<<(2+1)
a=(num<<2)+1;
int a,b,c;
cin>>a>>b;
c=a+b%10;//此处会识别成a+(b%10)
4.多组数据要初始化变量,局部变量要赋初值
特别是ans,sum不赋值等。
//比较好的习惯是将变量定义在循环内,从而求解每组数据时都能初始化变量
#include <stdio.h>
int sum;
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
//int sum=0;
//像上面这样定义变量就不会出事了
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int num;
scanf("%d",&num);
sum+=num;
}
printf("%d\n",sum);
}
return 0;
}
5.局部变量与全局变量冲突
建议全局变量多采取非常用的手误名称,如i,j,k,x,y,z是重灾区。
6.边界判断&&特判
for(int i=0;<;)
for(int i=1;<=;)
//注意循环边界范围,特别是数组是从0还是1开始记录的
### 9.是否使用了正确的文件io
```cpp
freopen("t1.in","r",stdin);
freopen("t1.out","w",stdout);
10.是否有正确的头文件和return
非void函数一定要有return,主函数要有return 0;
11.数据大小判断 是否可能爆int。以及int数据范围
int:256mb=6.7kwint;
int: 2e9;
12.不要使用x1,x2会卡变量名
13.检查文件名字!!
turn不等于trun
14.-o2看一下有什么不同的变化
15.注意使用的输入输出格式中会不会有空白
getchar会读入空行和空格
scanf:%c会读入空白,“ %c”是可行的
%s,&s[i]+1;//等同于cin>>s[i]+1;
16.while(scanf("[t++]")!=EOF) 天坑!t会多一个
17."no"是字母O不是零0
18.函数命名和调用,封装名称一致,数据类型一致
19.科学计数法1e9是一个浮点数
20.读题要仔细
子串是连续的;
子序列是不连续的,但是有先后之分;
子集既不连续,也无先后之分
21.sort是左闭右开区间
sort(a,a+n);//sort a[0]->a[n-1]
sort(a+1,a+1+n);//sort a[1]->a[n];