空间索引Spatial Indexing
 李喆
叫我桔子吧 PhD (Database)
148 人赞同了该文章
李喆
叫我桔子吧 PhD (Database)
148 人赞同了该文章
大家第一次接触到index应该是在上数据库这门课的时候。之所以数据库需要index,主要是因为数据量和应用层面的操作这两个原因,缺一不可。回忆下数据库最基本的操作:增删改查以及稍复杂些的比如连接操作,基本都需要先锁定数据位置,再执行操作。而定位这个步骤,如果没有index,基本都是O(n)的时间复杂度,这是一个非常“耗时”的操作。虽然从复杂度角度并不能算高,但是数据库访问是非常基础非常频繁的操作,性能直接影响到终端用户。所以非常微小的提升都是非常必要的。(如果是对于数据挖掘的算法,这类算法的用户通常是研究人员,那算法的速度快慢则显得非常次要,而accuracy则更为重要)。上面说,数据量大是使用index的一个原因,那为什么现在大量的机器学习算法,那些需要海量数据的算法不需要index呢?因为这些数据都是用来training或testing,而在这些步骤中,不需要预先定位数据位置。除了个别算法,比如KNN算法的prediction步骤,需要找到K个最近邻来判断给定item的label属性。“找”这个操作就需要定位。注意这里的定位不再是指在存储器上的位置,而是在空间中的位置,这里的空间,是由数据的维度张成的空间。空间数据,也即是这些拥有多维度的数据。这是空间数据的一个比较延展性的说法。但通常,空间数据都focus on 几何类型数据,比如点,线,面,球等,当然这些点、线都是可以任意维度的。对于空间数据的搜索,我们需要空间索引spatial index来提升搜素效率(速度)。目前主流数据库(SQL server, MySQL, PostgreSQL,etc)都已加入了对spatial data的支持,这其中最主要的就是数据类型和索引的支持。
R-tree
空间索引系列算法中最最最重要的就是R-tree了。R-tree由Guttman大神在1984年SIGMOD上提出。有时间的话我还是建议大家去感受下原文:
Guttman A. R-trees: A dynamic index structure for spatial searching[M]. ACM, 1984.
R-tree主要吸纳了B+tree的思想,对数据进行分割。已达到对数级访问时间。Guttman首先提出了MBR的概念,即Minimum Bounding Box。MBR的含义是用一个最小的矩形(通常默认矩形的边平行于坐标轴),来框住这个几何体。
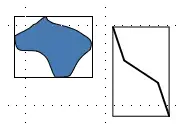 俩MBR
俩MBR
这样我们需要找到这个几何体中的一部分是,我们只需要先找到这个MBR即可。而找MBR这件事,则容易了很多。接下来,我们只需要用一个更大的MBR框住内层的小MBR,通过先找外层的MBR,我们可以很快找到内层MBR的大概位置。这个一层一层构建MBR的操作,非常类似B+tree的层。最后,我们就建立了一个空间上的分割。下图是一个二维R-tree的栗子。
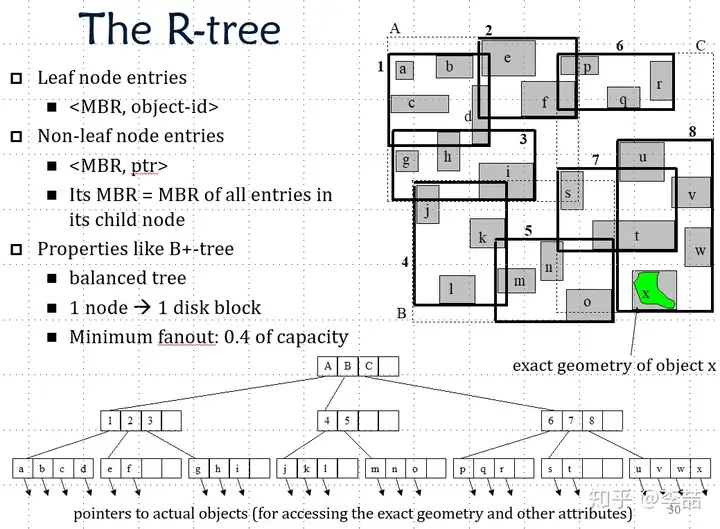 2-dimension R-tree example
2-dimension R-tree example
后续的研究比如R*-tree等对R-tree的提升主要是针对MBR的分割算法方面的。
kd-tree
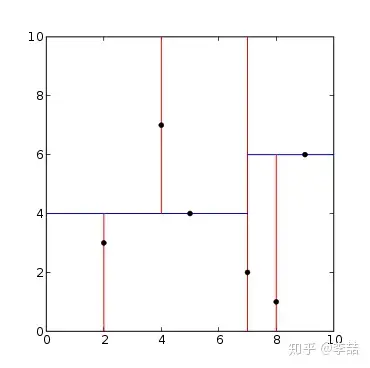 kd-tree
kd-tree
kd-tree的原理比R-tree要直接不少,对于k-dimension的数据,kd-tree的每一层,依次选一个维度把空间二分。对。。就这么简单。。。
Grid index
grid index即将要考虑的空间铺好网格,以便快速锁定区间。grid index尤其适合做最近邻搜索。毕竟只要考虑query所在grid的附近8个(2维时)grid就可以了。
oct-tree
八叉树是将3维空间的分成8份,依次再将每个子空间分成8份的操作,直到不需要再分为止。如果只在二维分的话,则每次分成四份,叫Quadtree。
虽然上述空间索引都很有效,但是当维度急剧提升时,空间索引的效率也会急剧下降。以R-tree为例,如果我们固定每个MBR最大容量为100,整个空间中有1M(million)个点,每个点的每个维度的范围是[0,1]。我们需要:1M/100 = 10000 个MBR。假设数据是均匀分布的。那么,设MBR边长为x,维度为n,则
标签:index,tree,Indexing,curve,索引,算法,Spatial,维度,MBR From: https://www.cnblogs.com/sexintercourse/p/18495368