2024/10/16 更新:
- 修改了状态的枚举方式,时间复杂度变为 \(O(3^n)\)。
前言
本篇题解默认您已熟练掌握最小生成树、状压 dp 及其应用,如果您还不会,请先阅读相关博客。
分析
我们要选出一条边,通过边转移能量,使得所有宝石的能量都为 \(0\)。
这看上去挺麻烦的,让我们挖掘一下题目的性质。可以发现:
-
传递时能量总和不会变。
-
每条边的花费和传递的能量的多少没有关系。
请读者注意这两条性质,可以发现,如果一个联通块的能量总和为 \(0\),则可以通过一系列的转移使得这个连通块的能量均为 \(0\)。
而要使一堆点联通,至少需要点数 \(-1\) 条边,这就形成了一棵树,而最优的答案就是最小生成树的权值和,我们可以用 Kruskal 算法解决。
那这道题是求整个图的最小生成树吗?显然不是,因为图不连通也可能更优。
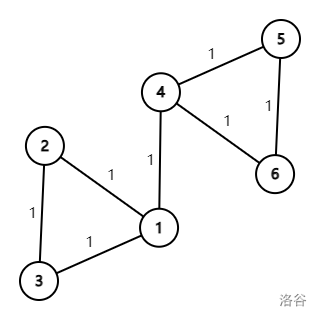
这里给出一个例子,其中点 \(1,2,3,4,5,6\) 的权值分别为 \(-5,-5,10,-5,-5,10\),边权已在图中标出。
如果我们求整个图的最小生成树,求出来的答案会是 \(5\),但是可以发现,我们选择 \(1-2,1-3,4-5,4-6\) 这四条边也同样可以满足条件,但花费减少到了 \(4\)。
这时候,数据范围就有用了,题目中 \(N\) 的范围为 \(1 \leq N \leq 16\)。我们就可以使用状压 dp 了。
设 \(s_i\) 表示状态为 \(i\) 时的能量总和,\(calc_i\) 表示状态为 \(i\) 时的最小生成树的花费,\(ans_i\) 表示状态为 \(i\) 时的答案。
显然,我们只需要在 \(s_i = 0\) 时才计算 \(calc_i\),因为在其他情况下计算 \(calc_i\) 并不会被 \(ans_i\) 用到。\(calc_i\) 能使用 Kruskal 算法计算。并且 \(calc_0=0\)。
接下来考虑计算答案,答案肯定由几个能量总和为零的连通块的答案相加而来,于是可以列出如下状态转移方程:
\[ans_i = \begin{cases} inf & s_i \ne 0 \\ \min_{j}^{s_j=0 \operatorname{and} j \in i}\{ans_{i \operatorname{xor} j} + calc_j\} & s_i = 0 \end{cases}\]其中 \(i,j\) 是枚举的状态。
初始 \(ans_0=0\)。
最终答案为 \(ans_{2^n-1}\)。
时间复杂度为 \(O(3^n)\)。
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define N 16
int n, m, a[N], fa[N], dep[N], s[1 << N], calc[1 << N], ans[1 << N];
struct stu
{
int u, v, w;
friend bool operator<(stu a, stu b)
{
return a.w < b.w;
}
} to[N * N];
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void merge(int x, int y)
{
x = find(x);
y = find(y);
if (x == y)
{
return;
}
if (dep[x] > dep[y])
{
fa[y] = x;
dep[x] += dep[y];
}
else
{
fa[x] = y;
dep[y] += dep[x];
}
}
int init(int x)
{
for (int i = 0; i < n; i++)
{
fa[i] = i;
dep[i] = 1;
}
int sum = __builtin_popcount(x) - 1, as = 0;
if (sum <= 0)
{
return 0;
}
for (int i = 0; i < m; i++)
{
int u = to[i].u, v = to[i].v, w = to[i].w;
if ((!(x & (1 << u))) || (!(x & (1 << v))))
{
continue;
}
if (find(u) == find(v))
{
continue;
}
sum--;
as += w;
merge(u, v);
if (!sum)
{
break;
}
}
if (sum != 0)
{
return 0x1f1f1f1f1f1f1f1f;
}
else
{
return as;
}
}
signed main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
for (int i = 1; i < (1 << n); i++)
{
for (int j = 0; j < n; j++)
{
if (i & (1 << j))
{
s[i] += a[j];
}
}
}
for (int i = 0; i < m; i++)
{
cin >> to[i].u >> to[i].v >> to[i].w;
}
sort(to, to + m);
memset(calc, 0x1f, sizeof(calc));
calc[0] = 0;
for (int i = 1; i < (1 << n); i++)
{
if (s[i] == 0)
{
calc[i] = init(i);
}
}
memset(ans, 0x1f, sizeof(ans));
ans[0] = 0;
for (int i = 0; i < (1 << n); i++)
{
if (s[i] == 0)
{
for (int j = i; j; j = (j - 1) & i)
{
ans[i] = min(ans[i], ans[i ^ j] + calc[j]);
}
}
}
int ANS = ans[(1 << n) - 1];
if (ANS >= 1e15)
{
cout << "Impossible";
return 0;
}
cout << ANS << endl;
return 0;
}
通过仅用时 47ms。
标签:dep,P10949,fa,魔杖,题解,int,ans,能量,calc From: https://www.cnblogs.com/awmmmmmm/p/18493708