左程云讲解102

加了fail指针的前缀树

通过在前缀树上构建fail指针，如下图，abcda，abcdb，bcdc

如果我要查询的是abcdcdc

先顺着1234号结点向下，abcdc，遇到最后的c时当前串上找不到了，通过fail跳到bcdc串上，因为abcd后缀和bcdc前缀重合，这么跳能减少重新匹配的成本

相当于对于要查询的串，我先从0位置开始，找abcbc找不到，那么继续从1为止开始，bcdc找得到，那么10结点答案+1，表示bcdc词频+1

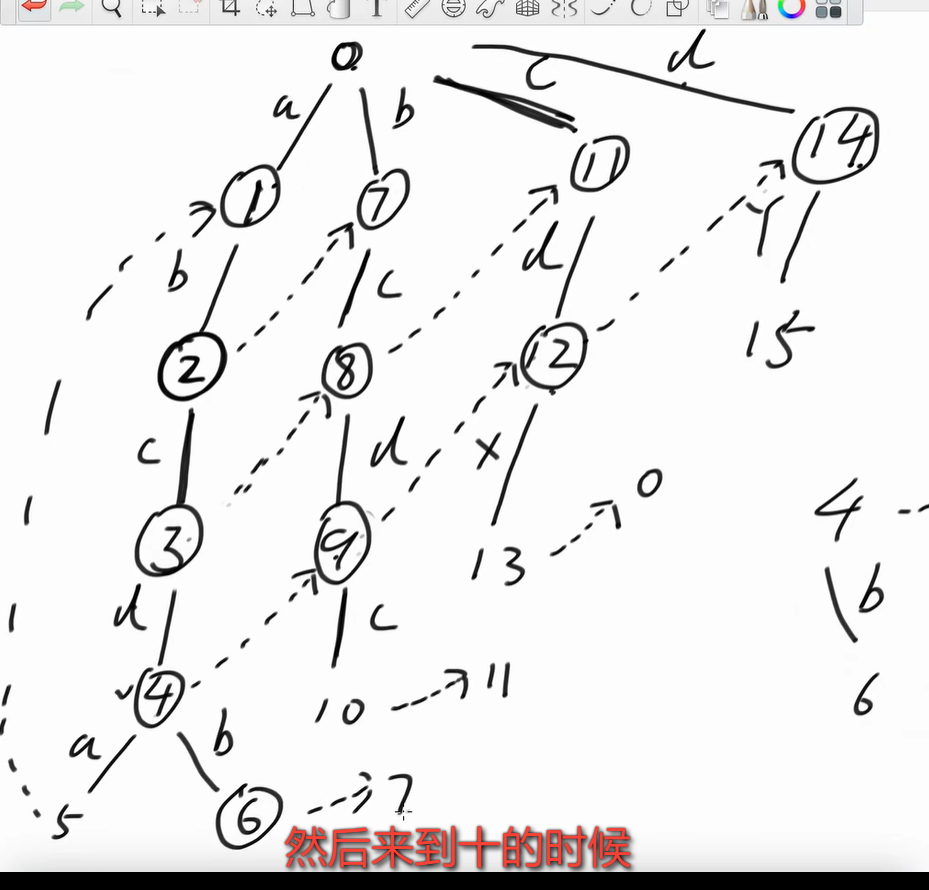
保留所有匹配成功的可能性

优化

优化1

问题：fail在构建的时候，遇到匹配不到的会往上跳再往下跳

解决方案：插入的次数较多，会出现重复跳同一条路径，那么在构建trie时，直接在表中将跳到的点构建好，实现使用功能时一次跳转到位，相当于把trie变成直通表，以后只要跳一次

优化2

问题：查询时候，每次到一个点都需要把往上的所有fail词频+1，但是如果反复经过一个词频，就需要反复走同一条路径

所以如下图所示，先只处理结点

完毕后根据fail建立反图，那么某个节点的贡献就是子树的贡献和

CODE

// #pragma GCC optimize(2)
// P5357 【模板】AC 自动机 https://www.luogu.com.cn/problem/P5357
#include <bits/stdc++.h>
using namespace std;

#define endl "\n"
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
#define rep(i, j, k) for (int i = (j); i < (k); i++)
#define all(x) x.begin(), x.end()
#define pii pair<int, int>

/* AC自动机 */
const int N = 2e5 + 10; // 目标字符串的数量，有存储终止节点编号的需求
const int S = 2e5 + 10; // 所有目标串的总字符数量
int ed[N];              // 每个目标串的结点编号 end
int tree[S][26];
int fail[S];
int cnt = 0; // 指针编号

/* 具体题目，本题为收集词频 */
int times[N];

/* 建反图，链式前向星 */
int edge = 0;
int head[S];
int nxt[S];
int to[S];
void addEdge(int u, int v) {
    nxt[++edge] = head[u];
    head[u] = edge;
    to[edge] = v;
}

inline int get(char ch) {
    return ch - 'a';
}

void insert(int i, string &s) {
    int p = 0;
    for (char ch : s) {
        int u = get(ch);
        if (!tree[p][u]) tree[p][u] = ++cnt;
        p = tree[p][u];
    }
    ed[i] = p;
}

void setFail() {
    queue<int> q;                  // BFS
    for (int i = 0; i < 26; i++) { // 0结点的子入队
        if (tree[0][i]) q.push(tree[0][i]);
    }
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = 0; i < 26; i++) {
            if (!tree[u][i]) { // 如果当前有节点，那么指向fail指针的对应子节点
                tree[u][i] = tree[fail[u]][i]; // 直通表的修改
            } else {/* 优化1部分 */
                // 有孩子，那么当前点的孩子（假定是b）的fail，需要指向当前点的fail指针的b孩子
                // 且因为是BFS的遍历，当前节点的fail一定是当前层或上层，是已经构建完毕的，不用担心有些fail的子节点没建好
                fail[tree[u][i]] = tree[fail[u]][i]; // 设置孩子的fail指针为自己fail指针的孩子
                q.push(tree[u][i]); // 正常步骤，将孩子加到队列中去
            }
        }
    }
}

// 汇总词频
void dfs(int u) {
    for (int e = head[u]; e != 0; e = nxt[e]) {
        dfs(to[e]);
        times[u] += times[to[e]];
    }
}

int main() {
    IOS;
    fill_n(times, S, 0);
    int n;
    cin >> n;
    rep(i, 1, n + 1) {
        string s;
        cin >> s;
        insert(i, s);
    }

    setFail();
    string t;
    cin >> t;

    for (int i = 0, u = 0; i < t.size(); i++) {
        int j = get(t[i]);
        u = tree[u][j];
        times[u]++;
    }

    for (int i = 1; i <= cnt; i++) { // 注意，是有多少tree的编号就add多少次
        addEdge(fail[i], i);
    }

    dfs(0);

    for (int i = 1; i <= n; i++) {
        cout << times[ed[i]] << endl;
    }
    
    return 0;
}