\(0+45+20+25=90\),T1 暴力写挂唐完了
显然催熟次数一定小于 \(n\),否则不会更优。对于催熟次数 \(k\) 确定时,每个种子能形成的其他种子一定如下图:
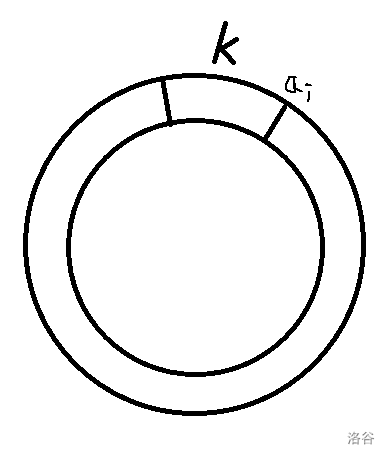
那么这就变成了一个滑动窗口板子。由于当催熟次数 \(k\) 递增时,催熟的价格线性递增,买种子的价格单调不增,且减量单调递增。两个函数复合后一定是一个下凸的丹枫单峰函数,直接三分即可
// BLuemoon_
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int kMaxN = 2e5 + 5;
LL n, k, a[kMaxN], l, r, mid;
deque<int> q;
LL Chk(int x, LL ret = 0) {
if (x == n + 1) {
return 1e18;
}
q.clear();
for (int i = n - x + 1; i <= n; i++) {
for (; !q.empty() && a[q.back()] >= a[i]; q.pop_back()) {
}
q.push_back(i);
}
for (int i = n + 1; i <= n << 1; i++) {
for (; !q.empty() && a[q.back()] >= a[i]; q.pop_back()) {
}
q.push_back(i), ret += a[q.front()];
for (; !q.empty() && q.front() <= i - x; q.pop_front()) {
}
}
return ret + k * x;
}
int main() {
freopen("collect.in", "r", stdin), freopen("collect.out", "w", stdout);
cin >> n >> k;
for (int i = 1; i <= n; i++) {
cin >> a[i], a[i + n] = a[i];
}
for (l = 0, r = n; l < r;) {
mid = (l + r) >> 1, (Chk(mid + 1) >= Chk(mid)) ? (r = mid) : (l = mid + 1);
}
cout << Chk(l) << '\n';
return 0;
}
令 \(f_i\) 为当 \(i\) 作为区间右端点时左端点最右在哪里,\(g_i\) 为当 \(i\) 为区间左端点时右端点最左在哪里,这部分可以用树状数组维护
然后就可以从这两个点跳,中间的就是满足条件的数量
// BLuemoon_
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int kMaxN = 2e5 + 5;
int n, a[kMaxN];
LL ans, f[kMaxN], g[kMaxN];
vector<int> v[kMaxN];
struct BIT {
LL mx[2][kMaxN], mn[2][kMaxN], sm[kMaxN];
BIT() { fill(mn[0], mn[2], 1e18), fill(mx[0], mx[2], -1e18); }
LL lb(LL x) { return x & -x; }
void Updatemx(int x, LL y, int t) {
for (; x <= n; mx[t][x] = max(mx[t][x], y), x += lb(x)){
}
}
void Updatemn(int x, LL y, int t) {
for (; x <= n; mn[t][x] = min(mn[t][x], y), x += lb(x)){
}
}
void Updatesm(int x, LL y) {
for (; x <= n; sm[x] += y, x += lb(x)){
}
}
LL Querymx(int x, int t, LL ret = -1e18) {
for (; x; ret = max(ret, mx[t][x]), x -= lb(x)) {
}
return ret;
}
LL Querymn(int x, int t, LL ret = 1e18) {
for (; x; ret = min(ret, mn[t][x]), x -= lb(x)) {
}
return ret;
}
LL Querysm(int x, LL ret = 0) {
for (; x; ret += sm[x], x -= lb(x)) {
}
return ret;
}
};
BIT tr;
int main() {
freopen("interval.in", "r", stdin), freopen("interval.out", "w", stdout);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
if (n <= 3) {
return cout << "0\n", 0;
}
for (int i = 1; i <= n; i++) {
f[i] = min(tr.Querymx(n + 1 - a[i], 0), tr.Querymx(a[i], 1)) - 1;
tr.Updatemx(n + 1 - a[i], i, 0), tr.Updatemx(a[i], i, 1);
}
for (int i = n; i; i--) {
g[i] = max(tr.Querymn(n + 1 - a[i], 0), tr.Querymn(a[i], 1)) + 1;
tr.Updatemn(n + 1 - a[i], i, 0), tr.Updatemn(a[i], i, 1);
}
for (int i = 1; i <= n; i++) {
(f[i] > 0) && (v[f[i]].push_back(i), 0);
}
for (int i = 1; i <= n; i++) {
(g[i] <= n) && (tr.Updatesm(g[i], 1), 0);
for (int j : v[i]) {
ans += tr.Querysm(j);
}
}
cout << ans << '\n';
return 0;
}
先考虑如何 \(O(26n)\) 求本质不同子序列个数
令 \(dp_{i,j}\) 为长度为 \(i\) 的前缀,以字符 \(j\) 结尾的本质不同子序列个数
那么如果 \(s_i\not=j\),\(dp_{i,j}=dp_{i-1,j}\),否则 \(dp_{i,j}=\displaystyle\sum_{i=1}^{26} dp_{i-1,j}\)
这个过程可以用矩乘优化,按上述 dp 模拟即可
// BLuemoon_
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int kMaxN = 500 + 5, kS = 26 + 5;
const LL kP = 1e9 + 7;
struct Mat {
LL a[kS][kS];
Mat operator*(const Mat &o) const {
Mat ret;
fill(ret.a[0], ret.a[kS], 0);
for (int i = 0; i <= 26; i++) {
for (int j = 0; j <= 26; j++) {
for (int k = 0; k <= 26; k++) {
(ret.a[i][k] += a[i][j] * o.a[j][k] % kP) %= kP;
}
}
}
return ret;
}
};
LL n, ans;
string s;
Mat cnt;
Mat Calc(int x) {
Mat ret;
fill(ret.a[0], ret.a[kS], 0);
for (int i = 0; i <= 26; i++) {
(i != x) && (ret.a[i][i] = 1);
if (i == x) {
for (int j = 0; j <= 26; j++) {
ret.a[i][j] = 1;
}
}
}
return ret;
}
int main() {
freopen("subseq.in", "r", stdin), freopen("subseq.out", "w", stdout);
cin >> n >> s, s = ' ' + s;
fill(cnt.a[0], cnt.a[kS], 0);
for (int i = 0; i <= 26; i++) {
cnt.a[i][i] = 1;
}
for (int i = n; i; i--) {
cnt = cnt * Calc(s[i] - 'a') * cnt;
}
for (int i = 0; i < 26; i++) {
(ans += cnt.a[i][26]) %= kP;
}
cout << ans << '\n';
return 0;
}
先抽出一颗 DFS 生成树,那么非树边一定是返祖边而非横跨边
\(k=1\) 是 tarjan 求割边板子,但是不好写,考虑树上差分
否则需要分类讨论:
- 若删除两条非树边,那么不会影响连通性
- 若删除一条割边,另外的边可以随便选,但要去掉两条割边互相选的情况
- 若删除一条非割边的树边
-
- 另一条边如果是非树边,这条非树边一定是唯一包含这条树边的返祖边,否则可以通过另一条返祖边维持连通性
-
- 如果另一条也是非割边的树边,图不连通的充要条件是包含这两条边的返祖边边集相同,这部分证明可以自己画图感性理解一下
-
-
- 对于充分性,删除这两条边,夹在这两条边之间的点就会被割掉
-
-
-
- 对于必要性,如果有一条只跨过其中一条树边的非树边,两边之间的点集就可以通过多出的这条边联通
-
那么除了最后一种情况,前面都可以通过树上差分解决,最后一种情况要用 xor-hashing 来求边集,遍历一遍 map 即可求出答案
// BLuemoon_
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int kMaxN = 2e5 + 5;
int n, m, k, u[kMaxN], v[kMaxN], s[kMaxN], dep[kMaxN];
vector<pair<int, int>> g[kMaxN];
LL ans;
unsigned long long e[kMaxN], o[kMaxN];
unordered_map<unsigned long long, LL> mp;
bitset<kMaxN> vis, f;
mt19937 Rand(time(0) / 2 + 3247);
void DFS(int u) {
for (auto [v, i] : g[u]) {
if (!vis[v]) {
vis[v] = 1, f[i] = 1, dep[v] = dep[u] + 1, DFS(v);
}
}
}
void DFS1(int u) {
for (auto [v, i] : g[u]) {
if (!vis[v]) {
vis[v] = 1, DFS1(v), s[u] += s[v];
}
}
}
void DFS2(int u) {
for (auto [v, i] : g[u]) {
if (!vis[v]) {
vis[v] = 1, DFS2(v), o[u] ^= o[v], mp[o[v]]++;
}
}
}
int main() {
freopen("attack.in", "r", stdin), freopen("attack.out", "w", stdout);
cin >> n >> m >> k;
for (int i = 1; i <= m; i++) {
cin >> u[i] >> v[i], g[u[i]].push_back({v[i], i}), g[v[i]].push_back({u[i], i});
}
vis[1] = 1, DFS(1);
for (int i = 1; i <= m; i++) {
(!f[i]) && (dep[v[i]] > dep[u[i]] ? (s[v[i]]++, s[u[i]]--) : (s[u[i]]++, s[v[i]]--));
}
vis.reset(), vis[1] = 1, DFS1(1);
for (int i = 2; i <= n; i++) {
ans += !s[i];
}
if (k == 1) {
return cout << ans << '\n', 0;
}
ans += (ans * (m - ans) + ans * (ans - 1) / 2);
for (int i = 2; i <= n; i++) {
ans += (s[i] == 1);
}
for (int i = 1; i <= m; i++) {
if (!f[i]) {
e[i] = uniform_int_distribution<unsigned long long>(0, 1e18)(Rand);
o[v[i]] ^= e[i], o[u[i]] ^= e[i];
}
}
vis.reset(), vis[1] = 1, DFS2(1);
for (auto [x, y] : mp) {
(x != 0) && (ans += y * (y - 1) / 2);
}
cout << ans << '\n';
return 0;
}