操作树加二分,目前题解区没有这种做法。
发现操作一可逆,可以用操作树,操作三解决。
操作一单点修改没什么好说的。
接下来看操作二。令 \(fa_{x,k}\) 为 \(x\) 的 \(k\) 级祖先。
发现对于每个询问中,如果 \(y\) 为奇数那么答案为 \(0\)。如果 \(y\) 为偶数,那么答案就是 \(fa_{x,y/2}\) 的 \(y/2\) 级儿子的开灯的个数减 \(fa_{x,y/2-1}\) 的 \(y/2-1\) 级儿子的开灯的个数。
具体实现方法就是先对这棵树跑出每个点的 bfs 序和 dfs 序,记树的第 \(i\) 层最大的 bfs 序为 \(lst_i\)。所有深度为 \(d\) 的点的 bfs 序都在 \([lst_{d-1}+1,lst_d]\),在这个区间二分。
举个例子:
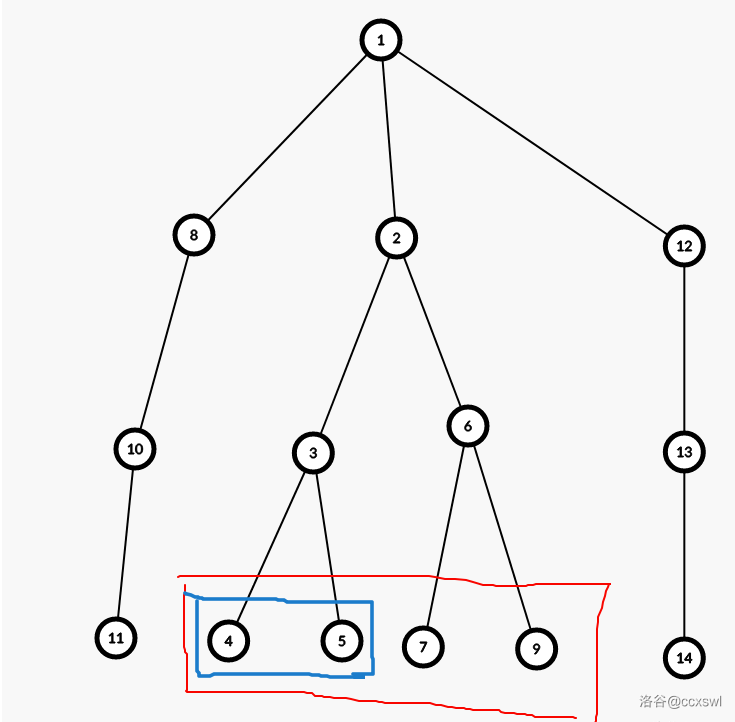
现在的询问 \(x=5,y=4\),那么 \(fa_{x,y/2}=2\),二分时如果二分出的点在以 \(fa_{x,y/2}\) 为根的子树内,视想要哪边的端点移动二分区间。如果不在这棵子树内,则与 \(fa_{x,y/2}\) 的 dfs 序比较。如果小,二分区间右移;如果大,二分区间左移。例如,目前二分到了 \(11\) 号节点,它的 dfs 序小于 \(2\) 的 dfs 序,那么二分区间右移。
最终答案为红色区间中的开灯个数减蓝色中的开灯个数。
用支持单点修改,区间求和的数据结构(例如树状数组)维护下就好了。
复杂度 \(O(n\log n)\)。
#include <bits/stdc++.h>
using namespace std;
int read() {
int s = 0, w = 1;
char c = getchar();
while (!isdigit(c)) {
if (c == '-')
w = -w;
c = getchar();
}
while (isdigit(c)) {
s = s * 10 + c - 48;
c = getchar();
}
return s * w;
}
void pr(int x) {
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
pr(x / 10);
putchar(x % 10 + 48);
}
#define end_ putchar('\n')
#define spc_ putchar(' ')
const int maxN = 1e5 + 7;
int n, m;
vector<int> E[maxN];
int bfn[maxN], dfn[maxN], tot;
int dep[maxN], siz[maxN], lst[maxN], rk[maxN];
int fa[25][maxN];
void dfs(int x, int f) {
dep[x] = dep[f] + 1;
siz[x] = 1;
dfn[x] = ++tot;
fa[0][x] = f;
for (int t = 1; t <= 20; t++)
fa[t][x] = fa[t - 1][fa[t - 1][x]];
for (int to : E[x])
if (to != f) {
dfs(to, x);
siz[x] += siz[to];
}
}
void bfs() {
tot = 0;
queue<int> Q;
Q.push(1);
while (!Q.empty()) {
int f = Q.front();
Q.pop();
bfn[f] = ++tot;
rk[tot] = f;
for (int to : E[f])
if (dep[to] > dep[f])
Q.push(to);
}
}
int find(int x, int k) {
for (int i = 0; k; i++, k >>= 1)
if (k & 1)
x = fa[i][x];
return x;
}
int cnt;
struct node {
int to, x, y, id;
node(int a, int b) {
to = a, x = b;
y = id = -1;
}
node(int a, int b, int c, int d) {
to = a, x = b, y = c, id = d;
}
};
vector<node> mo[maxN];
int qcnt;
struct ques {
int x, y, id;
};
vector<ques> q[maxN];
int ans[maxN];
int v[maxN];
int t[maxN];
void add(int x, int v) {
for (; x <= n; x += x & -x)
t[x] += v;
}
int ask(int x) {
int res = 0;
for (; x > 0; x -= x & -x)
res += t[x];
return res;
}
int solve(int x, int y) {
if (y == 0)
return v[x];
if (y & 1)
return 0;
y >>= 1;
int f = find(x, y);
if (!f)
return 0;
auto erfen = [x](bool ty, int f) {
int L = lst[dep[x] - 1] + 1, R = lst[dep[x]];
int ans = -1;
while (L <= R) {
int mid = (L + R) >> 1;
int p = rk[mid];
if (dfn[f] <= dfn[p] && dfn[p] <= dfn[f] + siz[f] - 1) {
ans = p;
if (ty)
R = mid - 1;
else
L = mid + 1;
}
else if (dfn[p] < dfn[f])
L = mid + 1;
else
R = mid - 1;
}
return ans;
};
int l = erfen(true, f), r = erfen(false, f);
int res = ask(bfn[r]) - ask(bfn[l] - 1);
f = find(x, y - 1);
l = erfen(true, f), r = erfen(false, f);
int tmp = ask(bfn[r]) - ask(bfn[l] - 1);
return res - tmp;
}
void calc(int x) {
for (auto i : mo[x]) {
if (i.x != -1 && i.id == -1) {
if (v[i.x])
v[i.x] = 0, add(bfn[i.x], -1);
else
v[i.x] = 1, add(bfn[i.x], 1);
}
if (i.id != -1)
ans[i.id] = solve(i.x, i.y);
calc(i.to);
if (i.x != -1 && i.id == -1) {
if (v[i.x])
v[i.x] = 0, add(bfn[i.x], -1);
else
v[i.x] = 1, add(bfn[i.x], 1);
}
}
}
int main() {
n = read();
for (int i = 1; i < n; i++) {
int u = read(), v = read();
E[u].push_back(v);
E[v].push_back(u);
}
dfs(1, 0);
bfs();
for (int i = 1; i <= n; i++)
lst[dep[i]] = max(lst[dep[i]], bfn[i]);
memset(ans, 255, sizeof(ans));
m = read();
for (int i = 1; i <= m; i++) {
int op = read();
if (op == 1) {
int x = read();
mo[cnt].emplace_back(cnt + 1, x);
++cnt;
}
if (op == 2) {
int x = read(), y = read();
mo[cnt].emplace_back(cnt + 1, x, y, i);
++cnt;
}
if (op == 3) {
int x = read();
mo[x].emplace_back(cnt + 1, -1);
++cnt;
}
}
calc(0);
for (int i = 1; i <= m; i++)
if (ans[i] != -1)
pr(ans[i]), end_;
}