昨晚码敲完了没保存,导致还原卡直接把我码肘没了。。。
气死了只能重新敲了一遍。
题面
分析
考虑每一个联通块分开处理。
先将每一个联通块变为生成树,任意生成方式皆可。
对于每一个联通块,一定可以构造一种组合方法,使得该联通块中最多只有一个关键点无法被选择。
并且每一个组合之间一定不会有重复的路径。因为如果有重复边,那么选择组合的时候就不会这么选了,如下图所示:
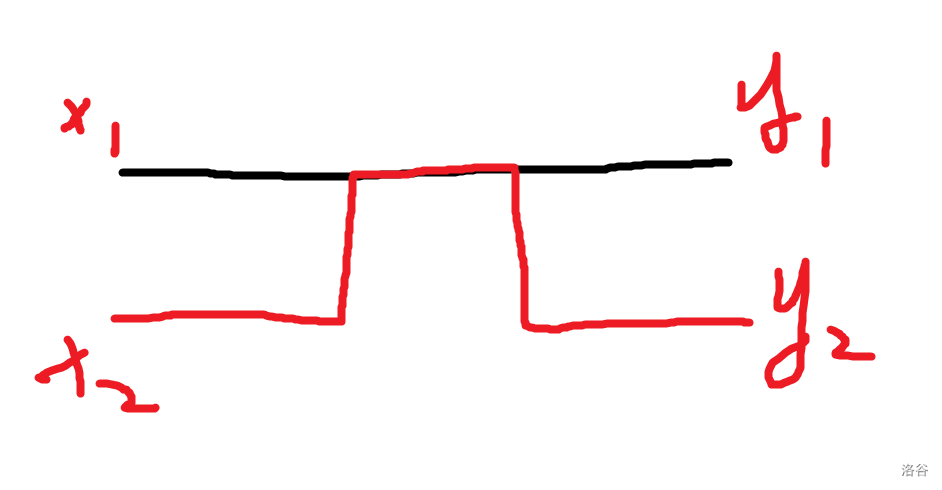
假设 $x_1$ 与 $y_1$ 是一对组合。
同时 $x_2$ 与 $y_2$ 组合与该组合有重复的部分。
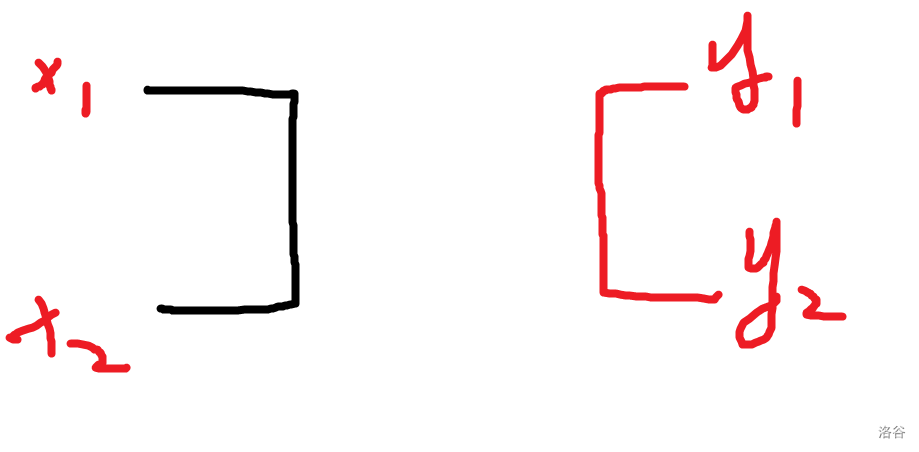
那么选择的时候就会选择 $x_1$ 与 $x_2$ 作为一对组合, $y_1$ 与 $y_2$ 作为一对组合,即可避免这种重复的情况,如下图:
找出所有组合之后,暴力求生成树上两点的距离就好了,可惜作者是个小呆呆,写了树剖,还没用上。。。
时间复杂度 $O(n)$。
谷还是交不了 codeforce 的题,好不容易切了一道黑题,白切了。
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct node
{
int nxt,to;
}edge[100010];
int head[100010],tot;
void add(int x,int y)
{
edge[++tot].nxt=head[x];
edge[tot].to=y;
head[x]=tot;
}
int n,m,k;
int book[100010];//k
int vis[100010];
int vis2[100010];
int dep[100010];
int size[100010];
int son[100010];
int top[100010];
int fa[100010];
pair<int,int>t[100010];
int cnt;
int dfs(int id,int f=0)
{
int hys=book[id]?id:0;
// cout<<id<<' '<<hys<<endl;
fa[id]=f;
dep[id]=dep[f]+1;
vis[id]=1;
size[id]=1;
for(int i=head[id];i;i=edge[i].nxt)
{
int to=edge[i].to;
if(vis[to])continue;
int xgd=dfs(to,id);
size[id]+=size[to];
if(xgd)
{
if(hys)
{
t[++cnt]=make_pair(xgd,hys);
hys=0;
}
else hys=xgd;
}
if(son[id]==0||size[son[id]]<size[to])
{
son[id]=to;
}
}
return hys;
}
void dfs2(int id,int topid)
{
vis2[id]=1;
top[id]=topid;
if(son[id])
{
dfs2(son[id],topid);
}
for(int i=head[id];i;i=edge[i].nxt)
{
int to=edge[i].to;
if(!vis2[to]&&to!=son[id])
{
dfs2(to,to);
}
}
}
int ans[100010],ans2[1000010];
int l1,l2;
void lca(int x,int y)
{
// cout<<x<<y<<endl;
l1=0,l2=0;
while(top[x]!=top[y])
{
// cout<<x<<y<<endl;
if(dep[top[x]]>=dep[top[y]])
{
int e=fa[top[x]];
for(;x!=e;x=fa[x])ans[++l1]=x;
}
else if(dep[top[x]]<dep[top[y]])
{
int e=fa[top[y]];
for(;y!=e;y=fa[y])ans2[++l2]=y;
}
}
if(dep[x]>dep[y])
{
for(;x!=y;x=fa[x])ans[++l1]=x;
}
else
{
for(;y!=x;y=fa[y])ans2[++l2]=y;
}
ans[++l1]=x;
printf("%lld ",l1+l2-1);
for(int i=1;i<=l1;i++)
{
printf("%lld ",ans[i]);
}
for(int i=l2;i>=1;i--)
{
printf("%lld ",ans2[i]);
}
putchar(10);
}
signed main()
{
scanf("%lld%lld%lld",&n,&m,&k);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%lld%lld",&u,&v);
// cout<<"QWQ";
add(u,v);
// cout<<"QWQ";
add(v,u);
// cout<<"QWQ";
}
for(int i=1;i<=k;i++)
{
int id;
scanf("%lld",&id);
book[id]=1;
}
for(int i=1;i<=n;i++)
{
if(!vis[i])
{
int qwq=dfs(i);
dfs2(i,i);
}
// cout<<dep[i];
}
printf("%lld\n",cnt);
for(int i=1;i<=cnt;i++)
{
int x=t[i].first,y=t[i].second;
if(x>y)swap(x,y);
lca(x,y);
// cout<<x<<y<<endl;
}
return 0;
}