个人认为思维难点相同的三倍经验:P3226 [HNOI2012] 集合选数、TFSETS - Triple-Free Sets。区别在于状压 DP 的方法。
我们称不包含质因子 \(2\) 和 \(3\) 的数为 \(2,3\texttt{-Free}\) 的。
对于 \([1,n]\) 内每个 \(2,3\texttt{-Free}\) 的整数 \(u\),可以列出以下的矩阵:
\[\begin{bmatrix} 2^03^0u & 2^03^1u & \cdots & 2^03^qu & \cdots \\ 2^13^0u & 2^13^1u & \cdots & 2^13^qu & \cdots \\ \vdots & \vdots & \ddots & \vdots & \ddots \\ 2^p3^0u & 2^p3^1u & \cdots & 2^p3^qu & \cdots \\ \vdots & \vdots & \ddots & \vdots & \ddots \\ \end{bmatrix} \]我们只保留矩阵中不超过 \(n\) 的元素,得到一个杨表。
例如,对于 \(n=12,u=1\) 的情况,对应的杨表如下:
\[\begin{bmatrix} 1 & 3 & 9 \\ 2 & 6 \\ 4 & 12 \\ \end{bmatrix} \]先考虑对于一个杨表,如何求出最少的操作次数,使得这个杨表中的所有数都在集合中。
容易发现,一次操作等价于选择一个数,把它、它右边、它下边共三个数覆盖,上述问题转化为最少选择多少个数,能覆盖整个杨表。
考虑轮廓线 DP。设 \(f_{i,j,S}\) 表示现在考虑到第 \(i\) 行第 \(j\) 列的格子(下标从 \(0\) 开始),轮廓线每个元素是否被覆盖的状态为 \(S\) 的最小操作次数。轮廓线的定义如下图所示。
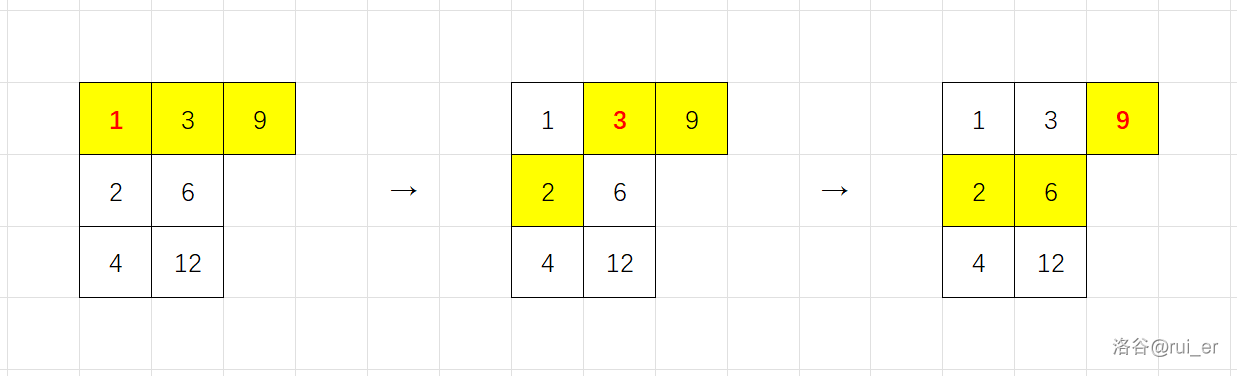
初始状态 \(f_{0,0,0}=0,f_{0,0,S}=+\infty\ (S\ne 0)\)。对于每个格子 \((i,j)\) 和状态 \(S\),若 \(S\) 中表明 \((i,j)\) 已被覆盖,则可以进行一次操作,或者不进行任何操作;若未被覆盖,则必须进行一次操作。容易写出转移方程,可以将 \(i,j\) 两维滚掉。
因此,对一个杨表求答案的时间复杂度 \(O(\log_2(\frac{n}{u})\log_3(\frac{n}{u})\times2^{\log_3(\frac{n}{u})})=O((\frac{n}{u})^{\log_32}\log^2(\frac{n}{u}))=O((\frac{n}{u})^{0.64}\log^2(\frac{n}{u}))\)。
显然,以每个 \(2,3\texttt{-Free}\) 的 \(u\) 作为杨表左上角,列出的元素互不相同。因此,答案即为每个 \(2,3\texttt{-Free}\) 的 \(u\) 作为杨表左上角的答案之和。
显然不能对于每个 \(2,3\texttt{-Free}\) 的 \(u\) 都求一遍答案。动用一下智慧,我们发现有大量的 \(u\) 对应的杨表形状是一样的,答案自然也是一样的。我们懒得考虑具体有多少种杨表形状,但是至少 \(\lfloor\frac{n}{u}\rfloor\) 相等的所有 \(u\) 的杨表形状肯定一样。记忆化一下,如果 \(\lfloor\frac{n}{u}\rfloor\) 与上一个杨表相同就不重复求答案,否则再跑轮廓线 DP 即可。
不会分析时间复杂度,但一看就不太大,不到 \(5\) 秒就跑完了。
另外,官方题解的 DP 部分好像跟我不一样,官方题解似乎用了子集卷积,我并没有特别理解。而我使用轮廓线 DP 可以直接规避子集卷积的知识,做到了相同的复杂度。
代码:
// Problem: B - 123 Set
// Contest: AtCoder - AtCoder Regular Contest 184
// URL: https://atcoder.jp/contests/arc184/tasks/arc184_b
// Memory Limit: 1024 MB
// Time Limit: 8000 ms
//
// Powered by CP Editor (https://cpeditor.org)
//By: OIer rui_er
#include <bits/stdc++.h>
#define rep(x, y, z) for(int x = (y); x <= (z); ++x)
#define per(x, y, z) for(int x = (y); x >= (z); --x)
#define debug(format...) fprintf(stderr, format)
#define fileIO(s) do {freopen(s".in", "r", stdin); freopen(s".out", "w", stdout);} while(false)
#define endl '\n'
using namespace std;
typedef long long ll;
mt19937 rnd(std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now().time_since_epoch()).count());
int randint(int L, int R) {
uniform_int_distribution<int> dist(L, R);
return dist(rnd);
}
template<typename T> void chkmin(T& x, T y) {if(y < x) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}
template<int mod>
inline unsigned int down(unsigned int x) {
return x >= mod ? x - mod : x;
}
template<int mod>
struct Modint {
unsigned int x;
Modint() = default;
Modint(unsigned int x) : x(x) {}
friend istream& operator>>(istream& in, Modint& a) {return in >> a.x;}
friend ostream& operator<<(ostream& out, Modint a) {return out << a.x;}
friend Modint operator+(Modint a, Modint b) {return down<mod>(a.x + b.x);}
friend Modint operator-(Modint a, Modint b) {return down<mod>(a.x - b.x + mod);}
friend Modint operator*(Modint a, Modint b) {return 1ULL * a.x * b.x % mod;}
friend Modint operator/(Modint a, Modint b) {return a * ~b;}
friend Modint operator^(Modint a, int b) {Modint ans = 1; for(; b; b >>= 1, a *= a) if(b & 1) ans *= a; return ans;}
friend Modint operator~(Modint a) {return a ^ (mod - 2);}
friend Modint operator-(Modint a) {return down<mod>(mod - a.x);}
friend Modint& operator+=(Modint& a, Modint b) {return a = a + b;}
friend Modint& operator-=(Modint& a, Modint b) {return a = a - b;}
friend Modint& operator*=(Modint& a, Modint b) {return a = a * b;}
friend Modint& operator/=(Modint& a, Modint b) {return a = a / b;}
friend Modint& operator^=(Modint& a, int b) {return a = a ^ b;}
friend Modint& operator++(Modint& a) {return a += 1;}
friend Modint operator++(Modint& a, int) {Modint x = a; a += 1; return x;}
friend Modint& operator--(Modint& a) {return a -= 1;}
friend Modint operator--(Modint& a, int) {Modint x = a; a -= 1; return x;}
friend bool operator==(Modint a, Modint b) {return a.x == b.x;}
friend bool operator!=(Modint a, Modint b) {return !(a == b);}
};
const int LOG2 = 30, LOG3 = 19, N = 1000000000, inf = 0x3f3f3f3f;
int n, btm, lim[LOG2], f[1 << LOG3], g[1 << LOG3], lst, mem, ans;
ll a[LOG2][LOG3];
void init(int x) {
btm = 0;
memset(lim, 0, sizeof(lim));
a[0][0] = x;
lim[0] = 0;
rep(j, 1, LOG3 - 1) {
a[0][j] = a[0][j - 1] * 3;
if(a[0][j] > n) break;
lim[0] = j;
}
rep(i, 1, LOG2 - 1) {
a[i][0] = a[i - 1][0] * 2;
if(a[i][0] > n) break;
lim[i] = 0;
++btm;
rep(j, 1, LOG3 - 1) {
a[i][j] = a[i][j - 1] * 3;
if(a[i][j] > n) break;
lim[i] = j;
}
}
}
int solve() {
rep(S, 0, (1 << LOG3) - 1) f[S] = +inf;
f[0] = 0;
rep(i, 0, btm) {
rep(j, 0, lim[i]) {
int U = (1 << (lim[i] + 1)) - 1;
rep(S, 0, U) g[S] = +inf;
if(j < lim[i]) {
rep(S, 0, U) {
if((S >> j) & 1) {
chkmin(g[S ^ (1 << j)], f[S]);
chkmin(g[S | (1 << j) | (1 << (j + 1))], f[S] + 1);
}
else chkmin(g[S | (1 << j) | (1 << (j + 1))], f[S] + 1);
}
}
else {
rep(S, 0, U) {
if((S >> j) & 1) {
chkmin(g[S ^ (1 << j)], f[S]);
chkmin(g[S | (1 << j)], f[S] + 1);
}
else chkmin(g[S | (1 << j)], f[S] + 1);
}
}
rep(S, 0, U) f[S] = g[S];
}
}
return *min_element(f, f + (1 << (lim[btm] + 1)));
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
rep(i, 1, n) {
if(i % 2 != 0 && i % 3 != 0) {
if(n / i != lst) {
lst = n / i;
init(i);
ans += (mem = solve());
}
else ans += mem;
}
}
cout << ans << endl;
return 0;
}