# Diverse Trajectory Forecasting with Determinantal Point Processes #paper
1. paper-info
1.1 Metadata
- Author:: [[Ye Yuan]], [[Kris Kitani]]
- 作者机构:: Carnegie Mellon University
- Keywords:: #HMP , #DPP
- Journal::
- Date:: [[2019-12-23]]
- 状态:: #Doing
- 链接:: http://arxiv.org/abs/1907.04967
1.2 Abstract
The ability to forecast a set of likely yet diverse possible future behaviors of an agent (e.g., future trajectories of a pedestrian) is essential for safety-critical perception systems (e.g., autonomous vehicles). In particular, a set of possible future behaviors generated by the system must be diverse to account for all possible outcomes in order to take necessary safety precautions. It is not sufficient to maintain a set of the most likely future outcomes because the set may only contain perturbations of a single outcome. While generative models such as variational autoencoders (VAEs) have been shown to be a powerful tool for learning a distribution over future trajectories, randomly drawn samples from the learned implicit likelihood model may not be diverse -- the likelihood model is derived from the training data distribution and the samples will concentrate around the major mode that has most data. In this work, we propose to learn a diversity sampling function (DSF) that generates a diverse and likely set of future trajectories. The DSF maps forecasting context features to a set of latent codes which can be decoded by a generative model (e.g., VAE) into a set of diverse trajectory samples. Concretely, the process of identifying the diverse set of samples is posed as a parameter estimation of the DSF. To learn the parameters of the DSF, the diversity of the trajectory samples is evaluated by a diversity loss based on a determinantal point process (DPP). Gradient descent is performed over the DSF parameters, which in turn move the latent codes of the sample set to find an optimal diverse and likely set of trajectories. Our method is a novel application of DPPs to optimize a set of items (trajectories) in continuous space. We demonstrate the diversity of the trajectories produced by our approach on both low-dimensional 2D trajectory data and high-dimensional human motion data.
a diverse yet likely set of future trajectories
diversity loss
DPPs
2. Introduction
- 领域
- Forecasting future trajectories of human
- 问题:
- 需要一个生成方法,该方法能够预测未来人体轨迹的多模态。
- 之前方法的缺点:
VAEs:- 随机采样,不能够采样到数据分布中的边缘特征。
VAE是基于条件概率的似然函数做encoder的,如果大多数数据以特定的模式为中心,那么其他模式的数据就很少。
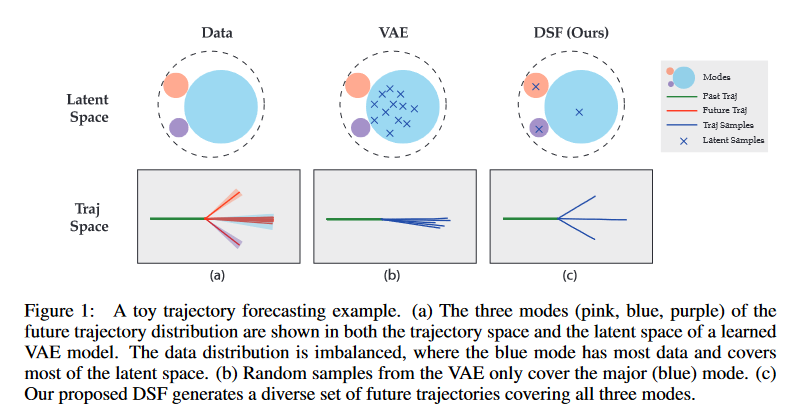
Figure. 1. A toy trajectory forecasting exampling
Source: http://arxiv.org/abs/1907.04967
Figure 1中的a, b说明了该问题。
- 作者的方法:
a diversity sampling function(DSF):能够进行多样化的可靠采样。- We propose a new forecasting approach that learns a diversity sampling function to produce a diverse set of future trajectories;
- We propose a novel application of DPPs to optimize a set of items (trajectories) in continuous space with a DPP-based diversity measure;
3. Approach
在一个预训练好的CVAE模型上,利用CVAE的decoder来产生多样性的生成。
多样性的保证通过一个DSF模型来选择具有多样性的潜在变量。
\(x \in \mathbb{R}^{T\times D}\):在\(T\)时刻(未来-待预测的时刻)的\(D\)维特征向量
\(\varphi=\{h,f\}\):
- \(h\in \mathbb{R}^{H\times D}\):表示历史\(H\)时间步长的信息。
- \(f\):其他边信息
3.1 Learning a CVAE for Future Trajectories
算法流程如下图

Figure.3. Training the cVAE
Source: http://arxiv.org/abs/1907.04967
CVAE:
- encoder: \(q_\phi (z|x,\varphi )\)
- decoder: \(p_\theta(x|z, \varPhi)\)
- loss: variational lower bound:
通过重参数技巧,并且两个高斯分布的KL散度能够直接计算
\[\mathcal{L}_{c v a e}(\mathbf{x}, \psi ; \theta, \phi)=-\frac{1}{V} \sum_{v=1}^{V}\left\|\tilde{\mathbf{x}}_{v}-\mathbf{x}\right\|^{2}+\beta \cdot \frac{1}{D_{z}} \sum_{j=1}^{D_{z}}\left(1+2 \log \sigma_{j}-\mu_{j}^{2}-\sigma_{j}^{2}\right) \]3.2 Diversity Sampling Function(DSF)
只通过CVAE模型,会丢失掉很多边缘特征,以至于无法生成多样化的轨迹。,于是作者提出了一种可学习的多样化采样方法。该方法利用DPP去生成最有效的最优子集。
算法伪代码:

Figure Training the diversity sampling function (DSF)
Source:
DSF:
- \(S_r(\varphi )\): 能够将\(\varphi\)映射成潜在变量集合\(\mathcal{Z}=\{z_1,..,z_N\}\)
- \(DPP kernel\):\(L = Diag(r)\cdot S \cdot Diag(r)\)
-
\(r\):定义了每个轨迹的质量
- \( r_{i}=\left\{\begin{array}{ll} \omega, & \text { if }\left\|\mathbf{z}_{i}\right\| \leq R \\ \omega \exp \left(-\mathbf{z}_{i}^{T} \mathbf{z}_{i}+R^{2}\right), & \text { otherwise } \end{array}\right. \)
-
\(S\):衡量两个不同轨迹的相似度
- \(S_{ij}=exp(-k\cdot d_x^2(x_i, x_j))\)
- \(d_x\):欧式距离
- \(k\) :scaling factor
- \(0 \le S_{ij} \le 1\) and \(s_{ii} = 1\)
- 正定矩阵
- \(S_{ij}=exp(-k\cdot d_x^2(x_i, x_j))\)
-
- Diversity Loss
- 如果使用
DPP log likelihood,表达式如下,该log likelihood会加重对重复项的惩罚,会造成数值问题。- if two trajectories inside Y are very similar, their corresponding rows in L will be almost identical, making det(L(γ)) = λ1λ2 . . . λN ≈ 0 (λn is the n-th eigenvalue). In practice, if the number of modes in the trajectory distribution p(x|ψ) is smaller than |Y|, Y will always have similar trajectories, thus making det(L(γ)) always close to zero. In such cases, optimizing the negative log likelihood causes numerical issues, which is observed in our early experiments.
expected cardinality of the DPP作为衡量多样性的度量。表达式如下- \( \mathbb{E}_{Y\sim \mathcal{P}_L(\mathcal{\gamma } ) }[|Y|] \)
- \( \mathbb{E}[|\boldsymbol{Y}|]=\sum_{n=1}^{N} \frac{\lambda_{n}}{\lambda_{n}+1}=\operatorname{tr}\left(\mathbf{I}-(\mathbf{L}(\gamma)+\mathbf{I})^{-1}\right) \)
- 于是作者定义的
diversity loss为\(\mathcal{L}_{\text {diverse }}(\gamma)=-\operatorname{tr}\left(\mathbf{I}-(\mathbf{L}(\gamma)+\mathbf{I})^{-1}\right)\)
- 如果使用
- Inference
- 推断过程的伪代码如下图

Figure.2. Inference with the DSF
Source: http://arxiv.org/abs/1907.04967
该算法过程的思想就是 利用贪心算法去对submodular function maximum问题进行求解。
submodular function:\(log det(L_{Y_f\cup \{x\}})\)
4. Experiments
实验需要解决的问题:
- 该方法是否能够比原始的
CVAE或者其他的baseline产生更多样性的采样数据? - 该方法在平衡数据和非平衡数据中的表现如何?
- 该方法是否能够处理低维度和高纬度的任务?
multi-modal evaluation:
Figure.4. 多模态说明
Source: http://arxiv.org/abs/1907.04967
在过去时刻具有相同上下文的\(\varphi^{(i)}|_{i=1}^N\) ,我们希望对这些相似的进行评估,而不是对单个进行评估。于是作者进行了如下的数据增强:
\[\mathcal{X}^{(i)}=\{x^{(j)}| \left \| \varphi ^{(j)}-\varphi ^{(i)} \right \|\le \varepsilon \},j=1,...,M \]- 评估指标
Average Displacement Error(ADE):average mean square error (MSE) over all time steps between the ground truth future trajectory x and the closest sample \(\tilde{x}\) in the forecasted set of trajectories \(Y_f\) .Final Displacement Error(FDE):between the final ground truth position xT and the closest sample’s final position \(\tilde{x} ^T\) .Average Self Distance(ASD):average L2 distance over all time steps between a forecasted sample \(\tilde{x}_i\)and its closest neighbor \(\tilde{x}_j\) in \(Y_f\) .Final Self Distance(FSD):L2 distance between the final position of a sample \(\tilde{x}_i ^T\)and its closest neighbor’s final position\(\tilde{x}_j ^T\).
ADE,FDE:用于评估生成未来序列的精确度。
ASD,FSD:用于衡量多样性和非重复性。
- Baseline
- Synthetic 2D Trajectory Data
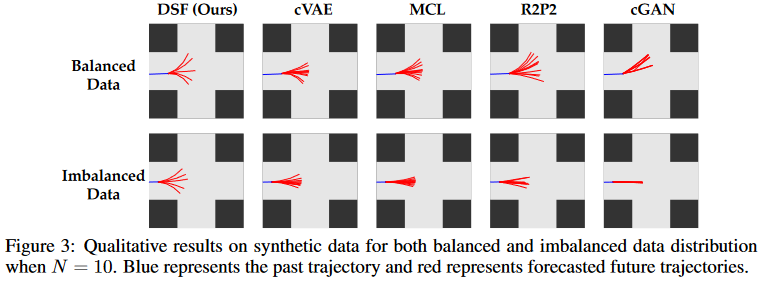
Figure.5. low-dimensional tasks
Source: http://arxiv.org/abs/1907.04967
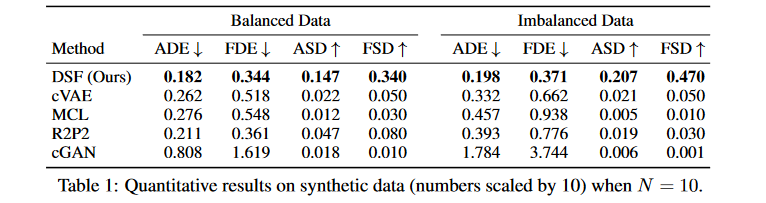
Figure.6. Quantitative results on synthetic data
Source: http://arxiv.org/abs/1907.04967
- Diverse Human Motion Forecasting

Figure.7. Quantitative results on for human motion forecasting
Source: http://arxiv.org/abs/1907.04967
- Additional Experiments with Diversity-based BaseLines
- datasets: Human3.6M
- baselines:
- DSF-NLL:a variant of DSF that uses NLL as the diversity loss instead of the expected cardinality.
- DSF-COS:a DSF variant that uses cosine similarity to build the similarity matrix S for the DPP kernel L.
- DSF-NLL:a variant of the cVAE that samples 100 latent codes and performs DPP MAP inference on the latent codes to obtain a diverse set of latent codes, which are then decoded into trajectory samples.
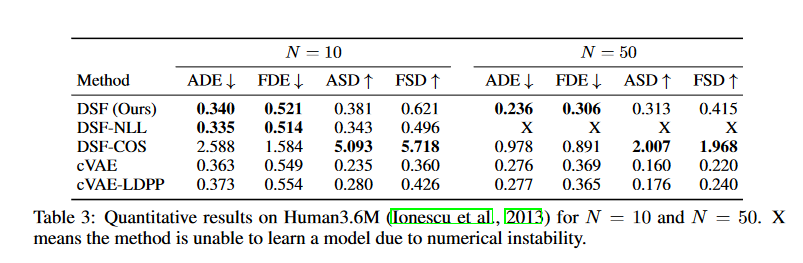
Figure.8. Quantitative results on Human3.6M
Source: http://arxiv.org/abs/1907.04967

Figure.9. Network architectures for synthetic data and human motion
Source: http://arxiv.org/abs/1907.04967
6. 总结
- 利用
cVAE的decoder - 结合
DPPs,利用训练好的decoder来优化多样性采样方法(DSF) - 利用DSF生成的潜在变量依然存在相似性,在测试阶段,通过贪婪算法,选择多样性最大的预测序列子集。