题意

给定一个 \(2\times N\) 的网格，网格上的点和上下左右连边。

要求支持以下几种操作：

• 修改某条边的边权。

• 求满足 \(y\in[l,r]\) 的点构成的点集的最小生成树。

分析

这道题的想法和 P4246 [SHOI2008] 堵塞的交通 很相似。

注意到 \(N, M \leq 6\times 10^4\)，并且查询的是 \(y\in[l,r]\) 的点构成的点集的最小生成树，考虑使用线段树维护。

我们考虑如何合并两个区间。

例如，下图的两个区间：

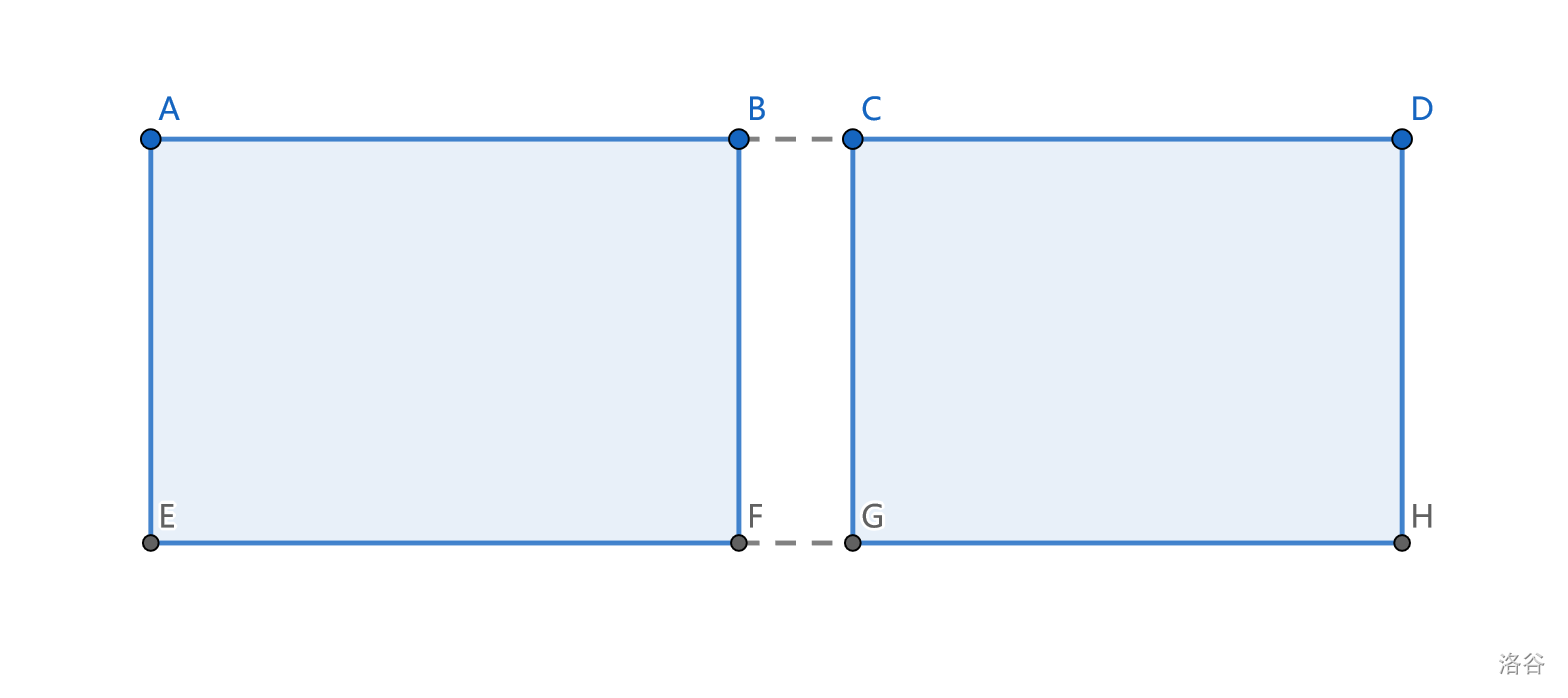
首先，我们将两个区间之间的边 \(BC, FG\) 加入这两个联通块中，让它们成为一个联通块。

因为 \(B\) 和 \(F\) 是联通的，\(C\) 和 \(G\) 是联通的，这样势必会形成一个环。

如图：

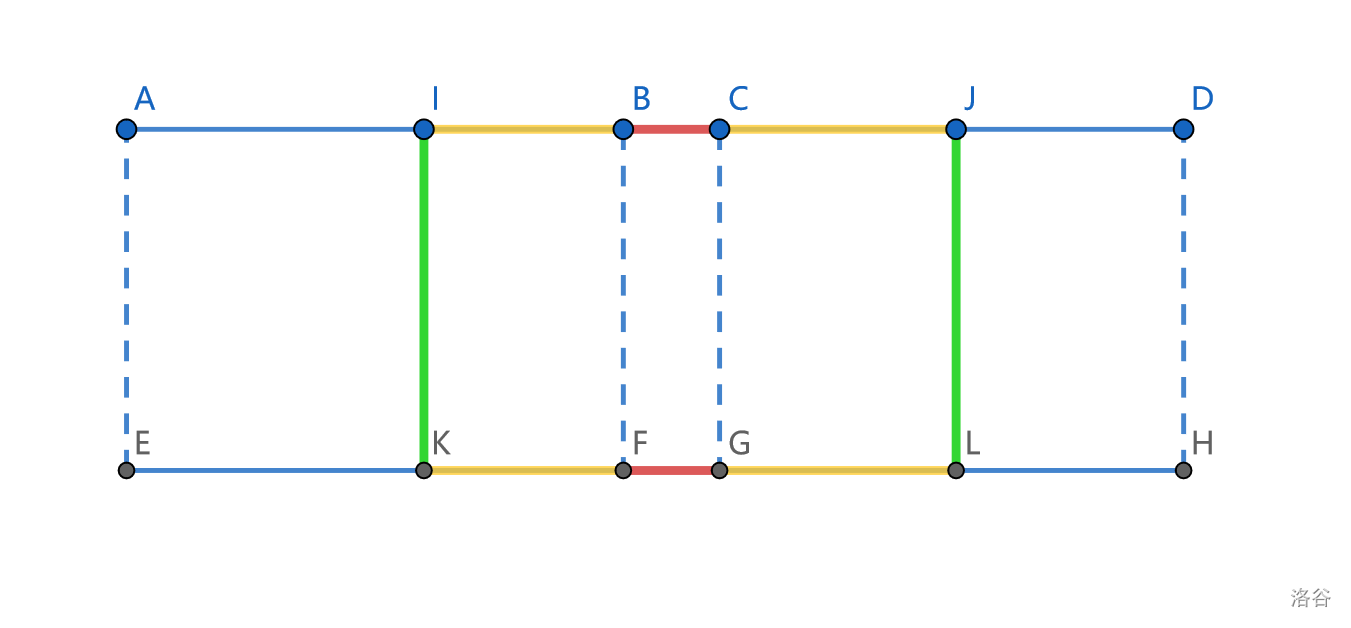
为了让它成为一棵树，我们需要删掉其中的一条边。

并且为了保证它是一棵最小生成树，我们应该删去边权最大的边。

到这里，我们维护的对象就显而易见了。

我们维护以下值：

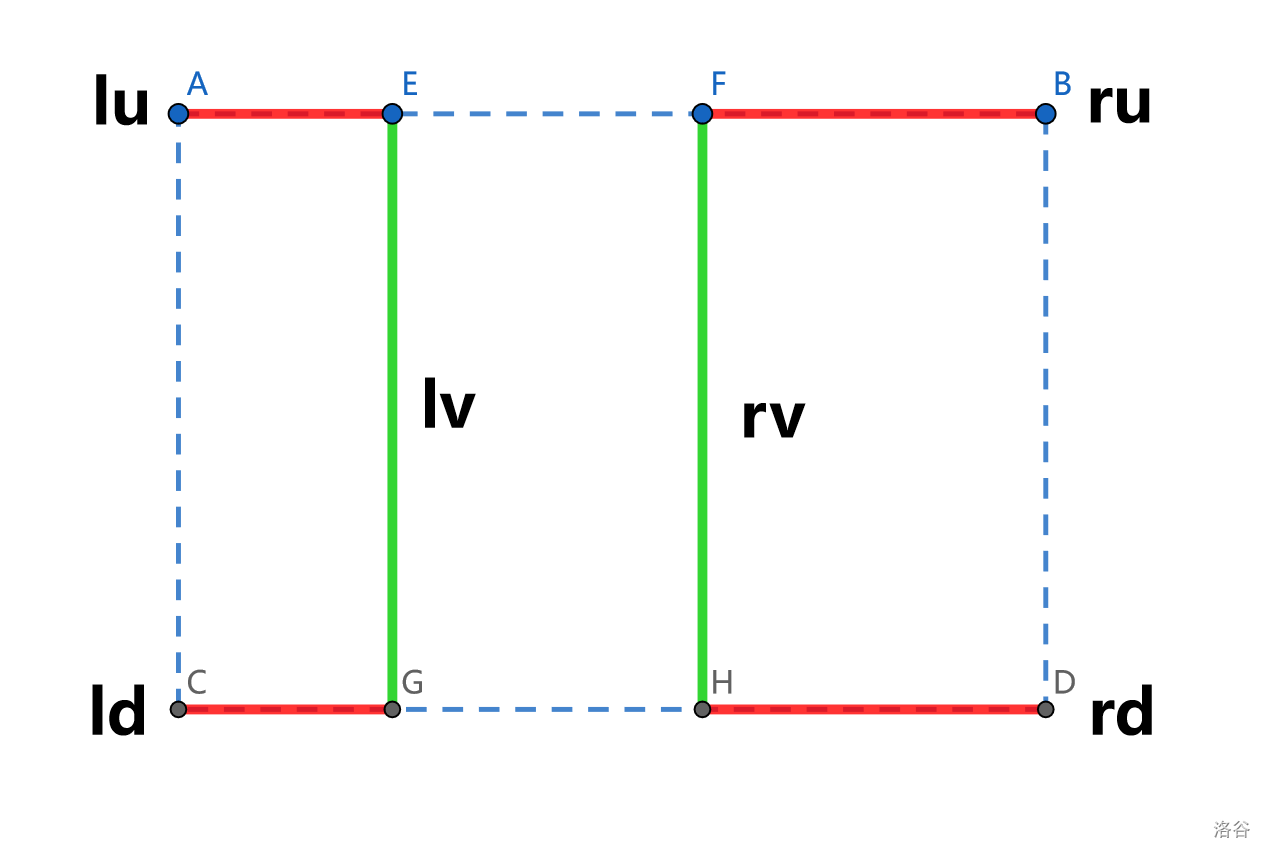
• lu：最左侧的垂直的生成树边上端点到左上角这一段中边的边权的最大值（即 \(AE\) 段中的边权最大值）
• ld：最左侧的垂直的生成树边下端点到左下角这一段中边的边权的最大值（即 \(CG\) 段中的边权最大值）
• ru：最右侧的垂直的生成树边上端点到右上角这一段中边的边权的最大值（即 \(BF\) 段中的边权最大值）
• rd：最右侧的垂直的生成树边下端点到右下角这一段中边的边权的最大值（即 \(DH\) 段中的边权最大值）
• lv：最左侧的垂直的生成树边的边权（即 \(EG\) 的边权）
• rv：最右侧的垂直的生成树边的边权（即 \(FH\) 的边权）
• ans：该段的最小生成树的边权和。

我们再回头看我们要合并的东西：

我们要删除的就是 \(IK,KF,FG,LG,JL,CJ,BC,IB\) 这些段中边权最小的一条边。

发现如果删除的是 \(KF,FG,LG,CJ,BC,IB\) 这些非垂直边，合并出的新段直接继承左右两端的信息即可。

但是如果删去了垂直边，可能出现某一侧区间没有垂直边的情况。

所以我们需要记录一个 cnt 来表示某个区间中有多少条垂直边。

假设左侧失去了垂直边，那么新区间的 lv 就应该是右区间的 lv，其他的信息同理。

Code

#include<bits/stdc++.h>
using namespace std;
#define maxn 60004

/*
lu           ru  vu
-+-+-+-+-+-+--- ==== ---+-+-+
   |       |            |  
  lv       rv           |  
   |       |            |  
-+-+-+-+-+-+--- ==== ---+-+-+
ld           rd  vd
*/

int vu[maxn], vd[maxn];

struct SegT
{
    struct node
    {
        int R, lv, rv, lu, ru, ld, rd, cnt, ans;
        node(int p=0, int v=0) {R=p, lv=rv=ans=v, lu=ru=ld=rd=0, cnt=1;}
        friend node operator+(node a, node b)
        {
            node ret;
            ret.R=b.R;
            ret.ans=a.ans+b.ans+vu[a.R]+vd[a.R];
            ret.cnt=a.cnt+b.cnt;
            int mx=max({vu[a.R], vd[a.R], a.ru, a.rd, b.lu, b.ld, a.rv, b.lv});
            ret.ans-=mx;
            ret.lv=a.lv, ret.rv=b.rv;
            ret.lu=a.lu, ret.ld=a.ld;
            ret.ru=b.ru, ret.rd=b.rd;
            if(mx==a.rv)
            {
                ret.cnt--;
                if(a.cnt==1)
                {
                    ret.lv=b.lv, ret.rv=b.rv;
                    ret.ld=max({a.ld, a.rd, b.ld, vd[a.R]});
                    ret.lu=max({a.lu, a.ru, b.lu, vu[a.R]});
                    ret.ru=b.ru, ret.rd=b.rd;
                }
            }
            else if(mx==b.lv)
            {
                ret.cnt--;
                if(b.cnt==1)
                {
                    ret.lv=a.lv, ret.rv=a.rv;
                    ret.rd=max({b.rd, b.ld, a.rd, vd[a.R]});
                    ret.ru=max({b.ru, b.lu, a.ru, vu[a.R]});
                    ret.lu=a.lu, ret.ld=a.ld;
                }
            }
            return ret;
        }
    }tr[maxn<<2];

    #define lc x<<1
    #define rc x<<1|1
    #define mid ((l+r)>>1)
    #define lson lc, l, mid
    #define rson rc, mid+1, r

    void modify(int x, int l, int r, int p, int v)
    {
        if(l==r) return tr[x]=node(p, v), void();
        if(p<=mid) modify(lson, p, v);
        if(p>mid)  modify(rson, p, v);
        tr[x]=tr[lc]+tr[rc];
    }

    void upd(int x, int l, int r, int p)
    {
        if(l==r) return;
        if(p<=mid) upd(lson, p);
        if(p>mid)  upd(rson, p);
        tr[x]=tr[lc]+tr[rc];
    }

    auto query(int x, int l, int r, int L, int R)
    {
        if(L<=l&&r<=R) return tr[x];
        if(R<=mid) return query(lson, L, R);
        if(L>mid)  return query(rson, L, R);
        return query(lson, L, R)+query(rson, L, R);
    }
}tr;

int main()
{
    int n, m;
    cin>>n>>m;
    for(int i=1;i<n;i++) cin>>vu[i];
    for(int i=1;i<n;i++) cin>>vd[i];
    for(int i=1, t;i<=n;i++)
    {
        cin>>t;
        tr.modify(1, 1, n, i, t);
    }
    char op;
    int x0, y0, x1, y1, w, L, R;
    while(m--)
    {
        cin>>op;
        if(op=='C')
        {
            cin>>x0>>y0>>x1>>y1>>w;
            if(x0==x1) (x0==1?vu:vd)[min(y0, y1)]=w, tr.upd(1, 1, n, min(y0, y1));
            else tr.modify(1, 1, n, y0, w);
        }
        if(op=='Q')
        {
            cin>>L>>R;
            cout<<tr.query(1, 1, n, L, R).ans<<'\n';
        }
    }
}