!
前置芝士:
二叉树的性质
\(1.\)二叉树中,第\(i\)层最多有\(2i-1\)个结点。
\(2.\)如果二叉树的深度为 \(K\),那么此二叉树最多有 \(2K-1\)个结点。
二叉树中,终端结点数(叶子结点数)为 \(n0\),度为 \(2\) 的结点数为 \(n2\),则 \(n0=n2+1。\)
\(3.\) 的计算方法为:对于一个二叉树来说,除了度为\(0\)的叶子结点和度为\(2\)的结点,剩下的就是度为 \(1\)的结点(设为 \(n1\)),那么总结点 \(n=n0+n1+n2\)。
同时,对于每一个结点来说都是由其父结点分支表示的,假设树中分枝数为 \(B\),那么总结点数 \(n=B+1\)。而分枝数是可以通过 \(n1\) 和 \(n2\) 表示的,即 \(B=n1+2*n2\)。所以,\(n\) 用另外一种方式表示为 \(n=n1+2*n2+1\)。
两种方式得到的 \(n\) 值组成一个方程组,就可以得出 \(n0=n2+1\)。
eg:
本题为较简单的树形dp
如此题若用
\(ls:p<<1\)
\(r:sp<<1|1\)
二叉树如果退化成一条链那需要开\(2^{5×10^5}\) 肯定会炸
所以可以直接记下ls与rs的编号(就像线段树的动态开点)
[ZJOI2006]三色二叉树
题目描述
一棵二叉树可以按照如下规则表示成一个由 \(0\)、\(1\)、\(2\) 组成的字符序列,我们称之为“二叉树序列 \(S\)”:
\[S= \begin{cases} 0& \text表示该树没有子节点\\ 1S_1& 表示该树有一个节点,S_1 为其子树的二叉树序列\\ 2S_1S_2& 表示该树由两个子节点,S_1 和 S_2 分别表示其两个子树的二叉树序列 \end{cases}\]例如,下图所表示的二叉树可以用二叉树序列 \(S=\texttt{21200110}\) 来表示。
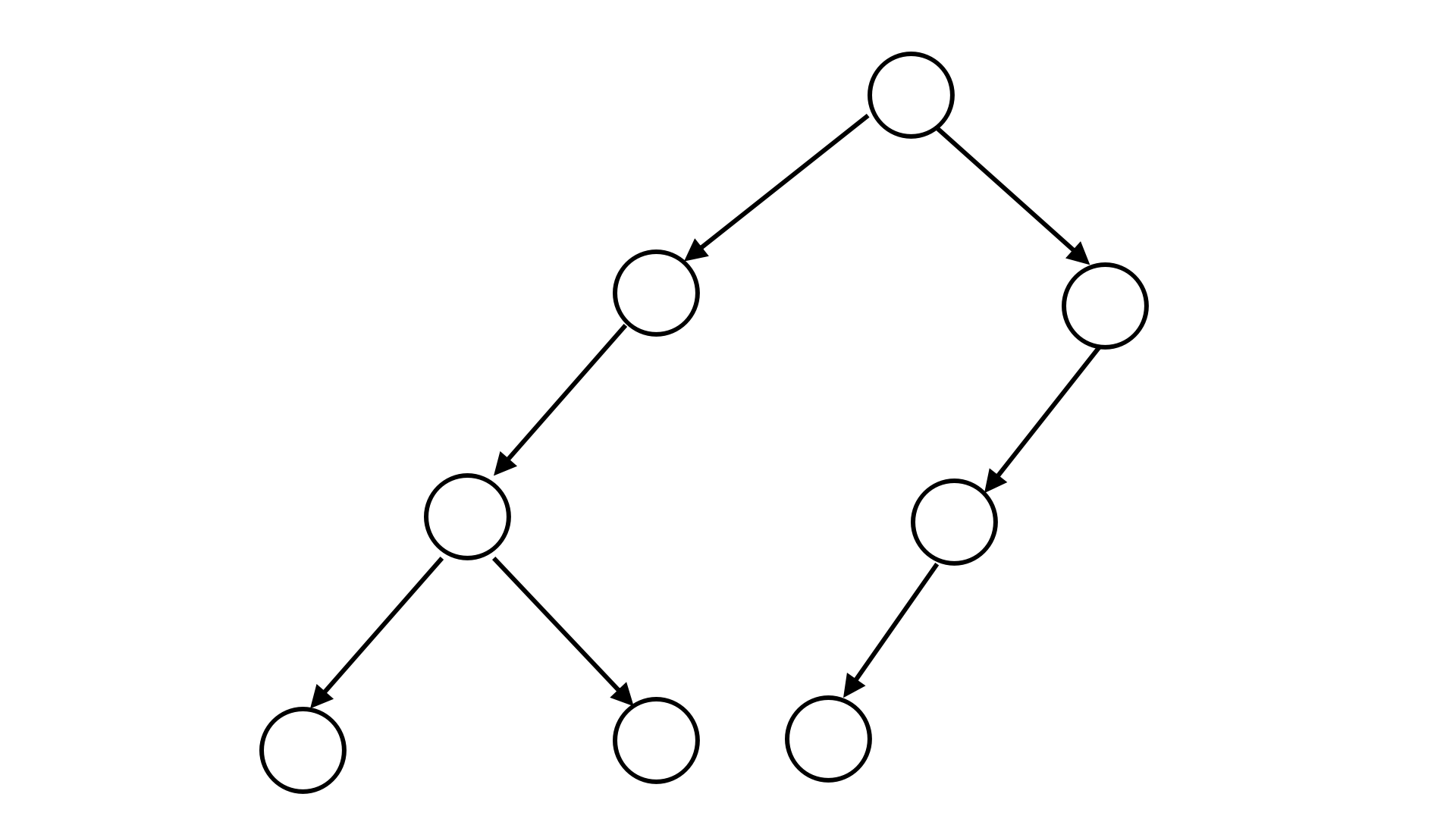
你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且,一个节点与其子节点的颜色必须不同,如果该节点有两个子节点,那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列,请求出这棵树中最多和最少有多少个点能够被染成绿色。
输入格式
输入只有一行一个字符串 \(s\),表示二叉树序列。
输出格式
输出只有一行,包含两个数,依次表示最多和最少有多少个点能够被染成绿色。
样例 #1
样例输入 #1
1122002010
样例输出 #1
5 2
提示
数据规模与约定
对于全部的测试点,保证 \(1 \leq |s| \leq 5 \times 10^5\),\(s\) 中只含字符 0 1 2。
标程:
#include<bits/stdc++.h>
using namespace std;
#define ls a[p].lson
#define rs a[p].rson
const int N = 5e5+9;
int n;
int f[N][3],ff[N][3];
struct node
{
int id,lson,rson;
}a[N];
int tot;
char s[N];
int k;
void build(int p)
{
a[p].id = s[++k]-'0';
if(a[p].id==1)
{
ls = ++tot;
build(ls);
}
else if(a[p].id == 2)
{
ls = ++tot;
rs = ++tot;
build(ls);
build(rs);
}
}
void dfs(int p)
{
if(a[p].id == 1)
{
dfs(ls);
f[p][0] = max(f[ls][1],f[ls][2])+1;
f[p][1] = max(f[ls][0],f[ls][2]);
f[p][2] = max(f[ls][0],f[ls][1]);
ff[p][0] = min(ff[ls][1],ff[ls][2])+1;
ff[p][1] = min(ff[ls][0],ff[ls][2]);
ff[p][2] = min(ff[ls][0],ff[ls][1]);
}
else if(a[p].id == 2)
{
dfs(ls),dfs(rs);
f[p][0] = max(f[ls][1]+f[rs][2],f[ls][2]+f[rs][1])+1;
f[p][1] = max(f[ls][0]+f[rs][2],f[ls][2]+f[rs][0]);
f[p][2] = max(f[ls][1]+f[rs][0],f[ls][0]+f[rs][1]);
ff[p][0] = min(ff[ls][1]+ff[rs][2],ff[ls][2]+ff[rs][1])+1;
ff[p][1] = min(ff[ls][0]+ff[rs][2],ff[ls][2]+ff[rs][0]);
ff[p][2] = min(ff[ls][1]+ff[rs][0],ff[ls][0]+ff[rs][1]);
}
else if(!a[p].id)
{
f[p][0] = 1;
ff[p][0] = 1;
}
}
int main()
{
scanf("%s",s+1);
build(++tot);
dfs(1);
printf("%d ",max(f[1][0],max(f[1][1],f[1][2])));
printf("%d",min(ff[1][0],min(ff[1][1],ff[1][2])));
return 0;
}