还是先复习,没有连续更新的原因是因为有一天满课,有一个家里有事情没有心情弄,不说了,好好干吧!
T31--扩展欧几里得
一.题目:
from Crypto.Util.number import *
flag = b'******'
m1 = bytes_to_long(flag[:len(flag)//2])
m2 = bytes_to_long(flag[len(flag)//2:])
assert 18608629446895353521310408885845687520013234781800558*m1-14258810472138345414555137649316815272478951117940067*m2 == 1
关键步骤:
assert 18608629446895353521310408885845687520013234781800558*m1-14258810472138345414555137649316815272478951117940067*m2 == 1
代码解释:
m1 = bytes_to_long(flag[:len(flag)//2])
m2 = bytes_to_long(flag[len(flag)//2:])
这段代码是Python语言编写的,主要用于将一个字节序列(bytes 类型)flag分成两部分,并将这两部分分别转换成长整型(int 类型,在Python 3中通常被称为“长整型”以区别于Python 2中的int和long,但实际上在Python 3中统一为int类型,可以处理任意大小的整数)。这种转换通常用于加密、解密、数据处理等领域,特别是在处理加密数据时,将字节序列转换为整数是一种常见做法。
下面是对这两行代码的详细解释:
flag[:len(flag)//2]
- 这部分代码使用了Python的切片操作。
flag是一个字节序列(bytes类型),len(flag)计算了flag的长度(即其中包含的字节数)。 len(flag)//2计算了flag长度的一半,注意这里使用了整除(//),意味着如果flag的长度是奇数,结果会向下取整。flag[:len(flag)//2]截取了flag从索引0开始到其长度一半(不包括一半处的索引)的子序列。
bytes_to_long(...)
- 这不是Python标准库中的一个函数,但可以假设它是一个自定义函数或来自某个第三方库,用于将字节序列转换为长整型(在Python 3中为
int)。 - 该函数的作用是将传入的字节序列作为二进制数据,将其转换为一个相应的长整型数。这通常是通过将字节序列视为一个大的二进制数,并直接将其转换为整数来实现的。
m1 = bytes_to_long(flag[:len(flag)//2])
- 这行代码首先使用切片操作从
flag中截取前半部分,然后将这部分转换为长整型,并将结果赋值给变量m1。
flag[len(flag)//2:]
- 这部分代码再次使用切片操作,但这次是从
flag长度的一半(包括一半处的索引,如果flag长度是奇数,则这一位也会被包括在内)到flag的末尾。
m2 = bytes_to_long(flag[len(flag)//2:])
- 这行代码将
flag的后半部分转换为长整型,并将结果赋值给变量m2。
总之,这两行代码将字节序列flag分为等长的两部分(如果flag的长度是奇数,则前半部分会比后半部分少一个字节),并将这两部分分别转换成长整型数,存储在变量m1和m2中。

二.解题思路以及代码
1.前置基础
欧几里得算法(辗转相除法)
解决问题:
将求两个数的最大公约数的时候转换为求比原来两个数小的最大公约(因)数
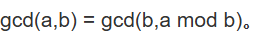
图解

举例
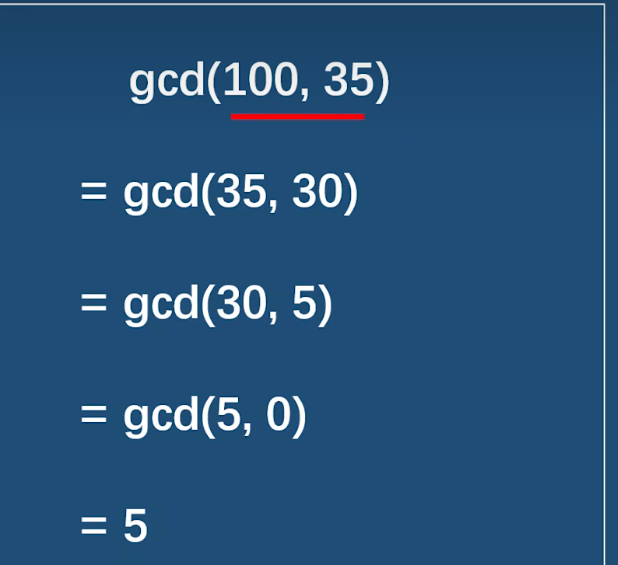
数学符号解释
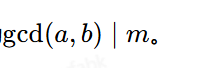
代表能整除m
扩展欧几里得算法
求出s和t(看懂下图)

s与t 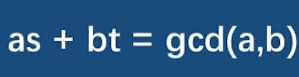

详细的算法自己去看
2.解题代码
from Crypto.Util.number import *
def extgcd(a, b):
if b == 0:
return a, 1, 0
g, x, y = extgcd(b, a%b)
return g, y, x - (a//b)*y
solve = extgcd(18608629446895353521310408885845687520013234781800558,14258810472138345414555137649316815272478951117940067)
a = abs(solve[1])
b = abs(solve[2])
for _ in range(10):
b += 18608629446895353521310408885845687520013234781800558
a += 14258810472138345414555137649316815272478951117940067
if b'NSSCTF' in long_to_bytes(a):
print(long_to_bytes(a)+long_to_bytes(b))
break
T32.高次Rabin
一.题目
from Crypto.Util.number import *
from gmpy2 import *
flag = b'NSSCTF{******}'
p = getPrime(256)
q = getPrime(256)
assert p%4 == 3 and q%4 == 3
n = p*q
e = 4
m = bytes_to_long(flag)
c = powmod(m, e, n)
print(f'p = {p}')
print(f'q = {q}')
print(f'e = {e}')
print(f'c = {c}')
'''
p = 59146104467364373868799971411233588834178779836823785905639649355194168174467
q = 78458230412463183024731868185916348923227701568297699614451375213784918571587
e = 4
c = 1203393285445255679455330581174083350744414151272999693874069337386260499408999133487149585390696161509841251500970131235102423165932460197848215104528310
'''
关键步骤:
assert p%4 == 3 and q%4 == 3
e = 4
可以看到rabin算法,但是e不是2,e=4,
二.wp
解题思路
将

解题代码
from Crypto.Util.number import *
p = 59146104467364373868799971411233588834178779836823785905639649355194168174467
q = 78458230412463183024731868185916348923227701568297699614451375213784918571587
e = 4
c = 1203393285445255679455330581174083350744414151272999693874069337386260499408999133487149585390696161509841251500970131235102423165932460197848215104528310
n = p*q
def rabin(c):
mp = pow(c, (p + 1) // 4, p)
mq = pow(c, (q + 1) // 4, q)
yp = inverse(p,q)
yq = inverse(q,p)
r = (yp * p * mq + yq * q * mp) % n
r_ = n - r
s = (yp * p * mq - yq * q * mp) % n
s_ = n - s
return r,r_,s,s_
c_list = rabin(c)
for c in c_list:
cc = rabin(c)
for c in cc:
flag = long_to_bytes(c)
if b'NSSCTF' in flag:
print(flag)
#NSSCTF{9c66047c-72da-49b6-9856-00fd46969fc7}
T41.Schemidt-Samoa非对称密码
一.题目:
from Crypto.Util.number import *
flag = b'NSSCTF{******}'
p = getPrime(512)
q = getPrime(512)
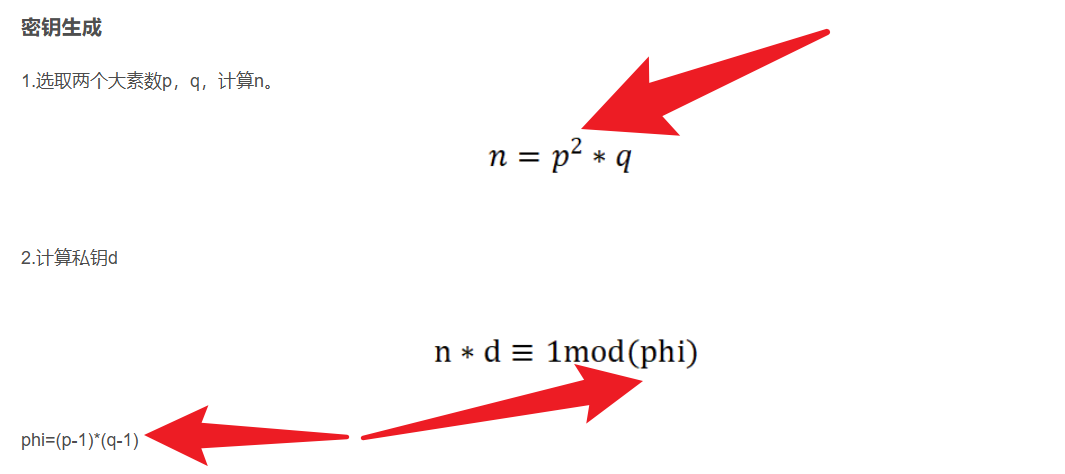
n = p*p*q
e = n
c = pow(bytes_to_long(flag), e, n)
d = inverse(e, (p-1)*(q-1))
print(f'n = {n}')
print(f'd = {d}')
print(f'c = {c}')
'''
n = 539403894871945779827202174061302970341082455928364137444962844359039924160163196863639732747261316352083923762760392277536591121706270680734175544093484423564223679628430671167864783270170316881238613070741410367403388936640139281272357761773388084534717028640788227350254140821128908338938211038299089224967666902522698905762169859839320277939509727532793553875254243396522340305880944219886874086251872580220405893975158782585205038779055706441633392356197489
d = 58169755386408729394668831947856757060407423126014928705447058468355548861569452522734305188388017764321018770435192767746145932739423507387500606563617116764196418533748380893094448060562081543927295828007016873588530479985728135015510171217414380395169021607415979109815455365309760152218352878885075237009
c = 192900246089028524753714085947506209686933390275949638288635203069117504901164350538204619142802436833736532680210208373707687461486601253665313637541968852691434282584934523173439632554783111037594035333325446559685553119339191110056283203940511701992217372405369575376549738295022767068810511670144120539082403063406787770958515441813335548550876818218065412869322721395317537328975187612606437225577060414403223288106406471061759010085578263501971809720648827
'''
关键步骤:
n = p*p*q
e = n
d = 58169755386408729394668831947856757060407423126014928705447058468355548861569452522734305188388017764321018770435192767746145932739423507387500606563617116764196418533748380893094448060562081543927295828007016873588530479985728135015510171217414380395169021607415979109815455365309760152218352878885075237009
p ^2*q,但是没有 pq
给了 d
e=n
二.解题思路以及代码
1. 前置知识:
Schmidt-Samoa密码系统,像rabin加密一样,其安全性基于整数因式分解的难度。但 Rabin 解密时会得到四个解,而 Schmidt-Samor 得到的是唯一解。
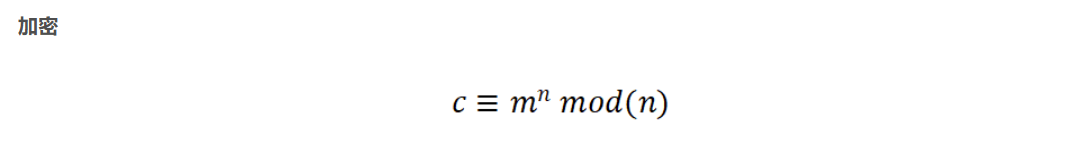
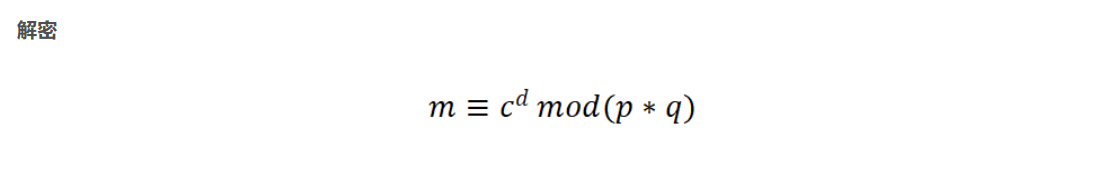
Xeeny 师傅
2. 解题思路
Schmidt-Samoa密码系统
3. 解题代码
from gmpy2 import *
from Crypto.Util.number import *
def getPQ(pub, priv):
return gmpy2.gcd(pub, gmpy2.powmod(2, pub*priv, pub)-2)
def decrypt(pub, priv, enc):
return gmpy2.powmod(enc, priv, getPQ(pub, priv))
n = 539403894871945779827202174061302970341082455928364137444962844359039924160163196863639732747261316352083923762760392277536591121706270680734175544093484423564223679628430671167864783270170316881238613070741410367403388936640139281272357761773388084534717028640788227350254140821128908338938211038299089224967666902522698905762169859839320277939509727532793553875254243396522340305880944219886874086251872580220405893975158782585205038779055706441633392356197489
d = 58169755386408729394668831947856757060407423126014928705447058468355548861569452522734305188388017764321018770435192767746145932739423507387500606563617116764196418533748380893094448060562081543927295828007016873588530479985728135015510171217414380395169021607415979109815455365309760152218352878885075237009
c = 192900246089028524753714085947506209686933390275949638288635203069117504901164350538204619142802436833736532680210208373707687461486601253665313637541968852691434282584934523173439632554783111037594035333325446559685553119339191110056283203940511701992217372405369575376549738295022767068810511670144120539082403063406787770958515441813335548550876818218065412869322721395317537328975187612606437225577060414403223288106406471061759010085578263501971809720648827
pq = getPQ(n, d)
m = decrypt(n, d, c)
print(long_to_bytes(m))
#NSSCTF{864098e7-7ef1-4c7e-90d6-d103d8c272e0}
三.相似题目
[GUET-CTF2019]Uncle Sam
from Crypto.Util.number import *
def generkey(k):
p, q = getPrime(k), getPrime(k)
pubkey = p**2 * q
n = pubkey
l = (p-1)*(q-1) / gcd(p-1, q-1)
privkey = inverse(n, l)
return pubkey, privkey
def encrypt(m, pubkey):
return pow(bytes_to_long(m), pubkey, pubkey)
# pubkey = 2188967977749378274223515689363599801320698247938997135947965550196681836543275429767581633044354412195352229175764784503562989045268075431206876726265968368605210824232207290410773979606662689866265612797103853982014198455433380266671856355564273196151136025319624636805659505233975208570409914054916955097594873702395812044506205943671404203774360656553350987491558491176962018842708476009578127303566834534914605109859995649555122751891647040448980718882755855420324482466559223748065037520788159654436293431470164057490350841209872489538460060216015196875136927502162027562546316560342464968237957692873588796640619530455268367136243313422579857823529592167101260779382665832380054690727358197646512896661216090677033395209196007249594394515130315041760988292009930675192749010228592156047159029095406021812884258810889225617544404799863903982758961208187042972047819358256866346758337277473016068375206319837317222523597
# privkey = 1430375790065574721602196196929651174572674429040725535698217207301881161695296519567051246290199551982286327831985649037584885137134580625982555634409225551121712376849579015320947279716204424716566222721338735256648873164510429206991141648646869378141312253135997851908862030990576004173514556541317395106924370019574216894560447817319669690140544728277302043783163888037836675290468320723215759693903569878293475447370766682477726453262771004872749335257953507469109966448126634101604029506006038527612917418016783711729800719387298398848370079742790126047329182349899824258355003200173612567191747851669220766603
# enc = 1491421391364871767357931639710394622399451019824572362288458431186299231664459957755422474433520889084351841298056066100216440853409346006657723086501921816381226292526490195810903459483318275931326433052468863850690793659405367902593999395060606972100169925074005992478583035226026829214443008941631771292291305226470216430735050944285543542354459162474346521327649934512511202470099020668235115245819634762067338432916012664452035696422865651002305445711778476072004708256200872226475346448360491248823843688268126341094612981308791499434770936360676087490303951728563482686307164877000300082742316368597958297217061375140696272398140310043942637287763946305961019518639745426370821124559939597559475362769382796386720030343305889701616194279058139516811941262747298761646317383112470923295543635754747288259324745583689440061956478083777663996487389553238481759103908588004219390662578446313004404784835263543083088327198
exp1
from gmpy2 import *
from Crypto.Util.number import *
def getPQ(pub, priv):
return gmpy2.gcd(pub, gmpy2.powmod(2, pub*priv, pub)-2)
def decrypt(pub, priv, enc):
return gmpy2.powmod(enc, priv, getPQ(pub, priv))
n= 2188967977749378274223515689363599801320698247938997135947965550196681836543275429767581633044354412195352229175764784503562989045268075431206876726265968368605210824232207290410773979606662689866265612797103853982014198455433380266671856355564273196151136025319624636805659505233975208570409914054916955097594873702395812044506205943671404203774360656553350987491558491176962018842708476009578127303566834534914605109859995649555122751891647040448980718882755855420324482466559223748065037520788159654436293431470164057490350841209872489538460060216015196875136927502162027562546316560342464968237957692873588796640619530455268367136243313422579857823529592167101260779382665832380054690727358197646512896661216090677033395209196007249594394515130315041760988292009930675192749010228592156047159029095406021812884258810889225617544404799863903982758961208187042972047819358256866346758337277473016068375206319837317222523597
d = 1430375790065574721602196196929651174572674429040725535698217207301881161695296519567051246290199551982286327831985649037584885137134580625982555634409225551121712376849579015320947279716204424716566222721338735256648873164510429206991141648646869378141312253135997851908862030990576004173514556541317395106924370019574216894560447817319669690140544728277302043783163888037836675290468320723215759693903569878293475447370766682477726453262771004872749335257953507469109966448126634101604029506006038527612917418016783711729800719387298398848370079742790126047329182349899824258355003200173612567191747851669220766603
c = 1491421391364871767357931639710394622399451019824572362288458431186299231664459957755422474433520889084351841298056066100216440853409346006657723086501921816381226292526490195810903459483318275931326433052468863850690793659405367902593999395060606972100169925074005992478583035226026829214443008941631771292291305226470216430735050944285543542354459162474346521327649934512511202470099020668235115245819634762067338432916012664452035696422865651002305445711778476072004708256200872226475346448360491248823843688268126341094612981308791499434770936360676087490303951728563482686307164877000300082742316368597958297217061375140696272398140310043942637287763946305961019518639745426370821124559939597559475362769382796386720030343305889701616194279058139516811941262747298761646317383112470923295543635754747288259324745583689440061956478083777663996487389553238481759103908588004219390662578446313004404784835263543083088327198
pq = getPQ(n, d)
m = decrypt(n, d, c)
print(long_to_bytes(m))
#flag{61e19444-7afb-11e9-b704-4ccc6adfc6f0}
exp2
from gmpy2 import*
from libnum import*
N = 2188967977749378274223515689363599801320698247938997135947965550196681836543275429767581633044354412195352229175764784503562989045268075431206876726265968368605210824232207290410773979606662689866265612797103853982014198455433380266671856355564273196151136025319624636805659505233975208570409914054916955097594873702395812044506205943671404203774360656553350987491558491176962018842708476009578127303566834534914605109859995649555122751891647040448980718882755855420324482466559223748065037520788159654436293431470164057490350841209872489538460060216015196875136927502162027562546316560342464968237957692873588796640619530455268367136243313422579857823529592167101260779382665832380054690727358197646512896661216090677033395209196007249594394515130315041760988292009930675192749010228592156047159029095406021812884258810889225617544404799863903982758961208187042972047819358256866346758337277473016068375206319837317222523597
#N = p^2*q
d = 1430375790065574721602196196929651174572674429040725535698217207301881161695296519567051246290199551982286327831985649037584885137134580625982555634409225551121712376849579015320947279716204424716566222721338735256648873164510429206991141648646869378141312253135997851908862030990576004173514556541317395106924370019574216894560447817319669690140544728277302043783163888037836675290468320723215759693903569878293475447370766682477726453262771004872749335257953507469109966448126634101604029506006038527612917418016783711729800719387298398848370079742790126047329182349899824258355003200173612567191747851669220766603
c = 1491421391364871767357931639710394622399451019824572362288458431186299231664459957755422474433520889084351841298056066100216440853409346006657723086501921816381226292526490195810903459483318275931326433052468863850690793659405367902593999395060606972100169925074005992478583035226026829214443008941631771292291305226470216430735050944285543542354459162474346521327649934512511202470099020668235115245819634762067338432916012664452035696422865651002305445711778476072004708256200872226475346448360491248823843688268126341094612981308791499434770936360676087490303951728563482686307164877000300082742316368597958297217061375140696272398140310043942637287763946305961019518639745426370821124559939597559475362769382796386720030343305889701616194279058139516811941262747298761646317383112470923295543635754747288259324745583689440061956478083777663996487389553238481759103908588004219390662578446313004404784835263543083088327198
pq = gcd(pow(2,d*N,N)-2,N)
m = pow(c,d,pq)
print(n2s(m))
#'flag{61e19444-7afb-11e9-b704-4ccc6adfc6f0}
T43.模多项式求根
一.题目
from Crypto.Util.number import *
flag = b'NSSCTF{******}'
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 3
m1 = bytes_to_long(flag)
a = getPrime(128)
b = getPrime(128)
m2 = a*m1 + b
c1 = pow(m1, e, n)
c2 = pow(m2, e, n)
print(f'n = {n}')
print(f'a = {a}')
print(f'b = {b}')
print(f'c1 = {c1}')
print(f'c2 = {c2}')
'''
n = 100458074154921630841467009716211081004496986067171453439200150708921645946139163766441611050743248698408002732330100522747315912617782265320913313460939731072047224701193946357341685422329349168512101723657005099845122860786073559690394636750367940135874243034107367507957642817011696553619030089913082650051
a = 235598638113466821523819951671842238817
b = 183046284622289531351267591814278208143
c1 = 59213026759461784288811267183372841532509333531605324857784387344377914885661521950844577998650904368265218037805476510488318417561718106578315758637105422183211905379616339980270327392640886739452625323181466064322246845738001714864060399808732460864513032069624364554351131806580712989439398464697132652674
c2 = 3451970836023636992808694960720139231990590529637727188690993996140273782744393239397467373679391223914185297028545706156586953463105320180151843119949047044046733716896796505869700601788410522957973779842899158545218190431782013633486273807312128458720848868027747769057989052968304813931468091592761421857
'''
关键步骤:
a = getPrime(128)
b = getPrime(128)
m2 = a*m1 + b
c1 = pow(m1, e, n)
c2 = pow(m2, e, n)
二.解题思路以及代码
1. 解题思路
推就完了

2. 解题代码
from gmpy2 import *
from Crypto.Util.number import *
n = 100458074154921630841467009716211081004496986067171453439200150708921645946139163766441611050743248698408002732330100522747315912617782265320913313460939731072047224701193946357341685422329349168512101723657005099845122860786073559690394636750367940135874243034107367507957642817011696553619030089913082650051
a = 235598638113466821523819951671842238817
b = 183046284622289531351267591814278208143
c1 = 59213026759461784288811267183372841532509333531605324857784387344377914885661521950844577998650904368265218037805476510488318417561718106578315758637105422183211905379616339980270327392640886739452625323181466064322246845738001714864060399808732460864513032069624364554351131806580712989439398464697132652674
c2 = 3451970836023636992808694960720139231990590529637727188690993996140273782744393239397467373679391223914185297028545706156586953463105320180151843119949047044046733716896796505869700601788410522957973779842899158545218190431782013633486273807312128458720848868027747769057989052968304813931468091592761421857
def get_m1(a, b, c1, c2, n):
a3 = pow(a, 3, n)
b3 = pow(b, 3, n)
tmp1 = ((c2 + 2*a3*c1 - b3) * b) % n
tmp2 = ((c2 - a3*c1 + 2*b3) * a) % n
tmp3 = invert(mpz(tmp2), mpz(n))
tmp4 = (tmp1 * tmp3) % n
return tmp4
m1 = get_m1(a, b, c1, c2, n)
flag = long_to_bytes(m1)
print(flag)
#b'NSSCTF{76f8044e-7bf9-43cd-885f-22f611628b8b}'
代码解释:(mpz(tmp2)
在Python中,mpz 通常不是直接可见的类或函数名,但它是GMPY2库(GNU Multiple Precision Arithmetic Library的Python接口)中用于表示大整数(multi-precision integers)的内部类型。GMPY2是一个用于高精度算术的Python库,它提供了比Python标准库中的int类型更高的性能和更大的范围。
然而,在GMPY2的Python接口中,你通常不会直接看到或操作mpz类型的对象,因为GMPY2会为你处理这些底层细节。相反,你会使用GMPY2提供的函数和类来创建和操作大整数。
如果你看到mpz(tmp2)这样的表达式,它可能是在讨论GMPY2的内部实现,或者是在查看GMPY2的源代码时遇到的。但在正常的GMPY2使用场景中,你不会直接这样写代码。
在GMPY2中,创建大整数通常很简单,比如:
import gmpy2
# 创建一个大整数
a = gmpy2.mpz(123456789012345678901234567890)
# 或者直接使用Python的int类型,GMPY2会自动处理
b = 123456789012345678901234567890
# 进行大整数运算
c = a + b
print(c)
在这个例子中,gmpy2.mpz()函数可以用来显式地创建一个mpz类型的大整数,但实际上,GMPY2非常智能,它会自动将Python的int类型转换为mpz类型(如果整数太大以至于Python的int类型无法表示),所以你通常不需要显式地调用gmpy2.mpz()。
如果你在处理与GMPY2相关的代码或文档,并且遇到了mpz(tmp2)这样的表达式,它可能是在说明某个变量tmp2被转换或视为一个mpz类型的大整数,但这并不是你在编写GMPY2代码时通常会使用的语法。
(这里有没有都能解出,暂时不清楚什情况)
结语:
对于密码学来说,不思考的学习是毫无意义的,不动脑子渴望进步就是扯淡,拜
标签:进阶,bytes,RSA,long,---,flag,m1,print,import From: https://www.cnblogs.com/yanxiao777/p/18399399
