标签：le int 火把 safe CEOI2023 区间考虑

Day1 T1 A Light Inconvenience (light)

题意：若干个人排成一个队列，保证任何时刻队列中都有至少一个人。每个人手中有一个火把，火把有点亮和熄灭两种状态。
现在进行 \(Q\) 次操作，每次操作形如在队列尾部加入或删除 \(p_0\) 个人，然后你需要选择一个 \(t_0\) 满足 \(t_0 \le p_0\)，然后对于每个火把点亮的人，将他后面的 \(t_0\) 个人的火把也点亮，然后再熄灭任意一些人的火把。此时我们称这次操作结束。
你需要保证，在每次操作结束时，最后一个人的火把是点亮的，并且点亮的火把数不超过 \(150\)。每次操作你需要给出你选择的 \(t_0\)，和当前哪些位置的火把是点亮的。
记 \(N\) 表示任意时刻队列中人数的最大值，保证 \(1 \le N \le 10^{17}, 1 \le Q \le 5 \times 10^4\)。

首先显然，我们每次会选择 \(t_0 = p_0\)，即对于每一个火把是点亮的人，我们会使他点亮右边的尽量多的人，这个很好理解，因为多点亮的火把可以在回合结束时熄灭。

考虑如果只有加入操作的话是好做的，我们只需保证最右边的人火把是亮着的，加入时向右转递，那么容易发现我们还是可以把最右边的人的火把点亮。

但是有删除操作我们就不好做了，考虑如果他将我们最右边的人删掉我们就寄了，那怎么办呢？很容易想到倍增，我们从右往左点亮火把，第 \(i\) 个火把与第 \(i - 1\) 个火把距离 \(2^{i - 1}\)，那么可以保证，无论删除多少个人，我们一定可以点亮最右边的人的火把。

这样构造的话，加入操作也很好维护，我们只需将所有人的火把状态向右平移，多出来的部分依然倍增即可。

但是删除操作又出现了一个问题，考虑直接二进制拆分相当于向左平移，但是火把是不能向左传递的。比如下面这张图：

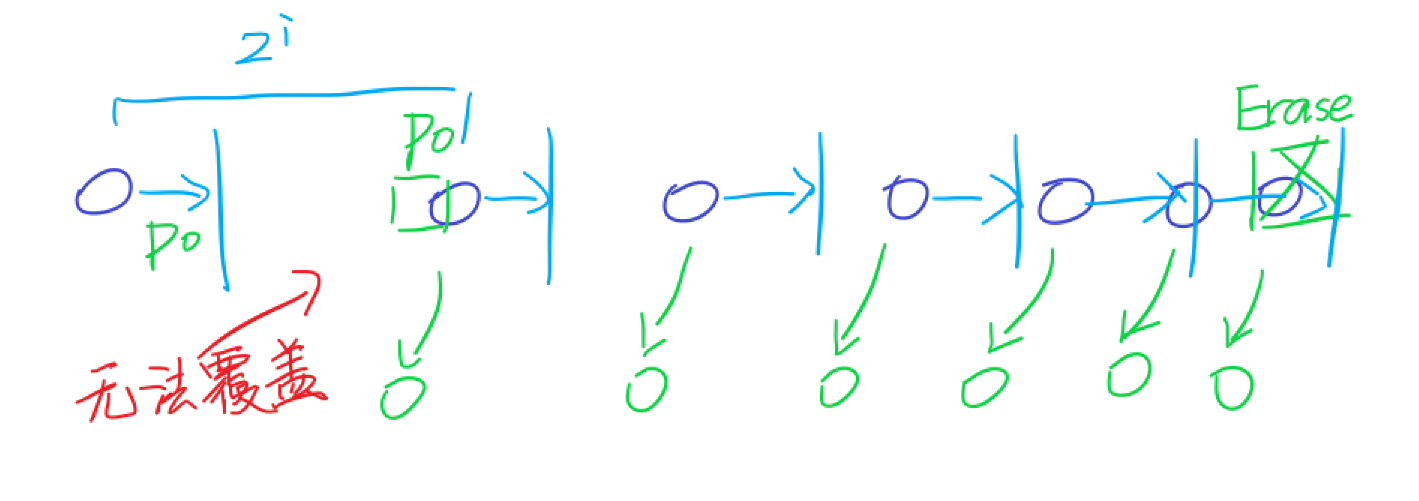
考虑一个点向右能覆盖的位置是 \(p_0\)，即任意给出的删除参数，但是两个位置之间的 gap 是 \(2^i\) 的，这个跟 \(p_0\) 没有半点关系，那么当 \(i\) 较大，\(p_0\) 较小的时候就会出现问题。

所以我们考虑贪心一下，改造这个构造方法：如果前面的数无法覆盖这个期望位置，就跳到上一种方案的第一个在它右边的位置。具体而言：

我们还是从右往左考虑点亮若干火把，设第 \(i\) 个点亮的火把与第 \(1\) 个点亮的火把之间的距离，显然 \(d_1 = 0\)，并且我们可以归纳的证明最右边的火把一定可以被点亮。
考虑已经点亮了 \([1, i]\) 中的所有火把，现在考虑加入第 \(i + 1\) 根火把，我们当然希望 \(d_{i + 1} = 2(d_i + 1)\)。
但是我们前面说明了，这样并不总是可行的，考虑令操作之前点亮的火把位置构成的序列为 \(f\)（从左到右标号），考虑找到最大的 \(j\)，满足 \(f_j\) 大于我们期望的位置，如果期望位置不可行则跳到 \(f_j\)，

可以证明，这样构造在回合结束时火把数量不超过 \(2 \log n + O(1)\)。下面使一个感性的证明：

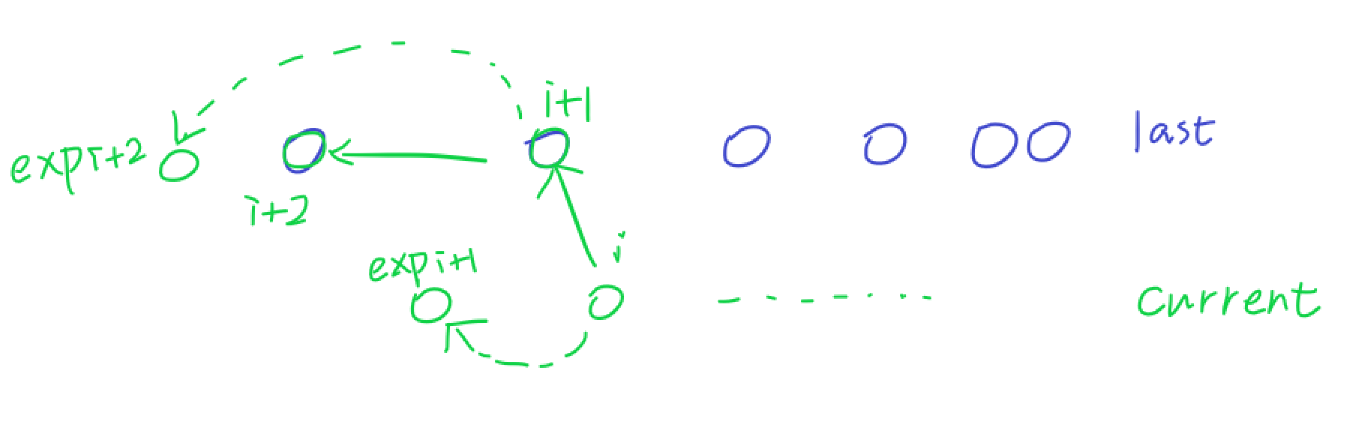
考虑 \(i + 1\) 是否跳到了期望位置 \(exp_{i + 1}\)，如果跳到了那么 \(d_{i + 1} = 2(d_{i} + 1)\)，当前火把离最右端火把远了一倍。
否则没跳到 \(exp_{i + 1}\)，考虑下一步怎么跳，如果跳到了 \(exp_{i + 2}\) 那么是一样的，当前火把离最右端火把又远了一倍。
那么我们可以说明 \(i + 2 < exp_{i + 1}\) 的，否则会直接从 \(i\) 跳到 \(i + 2\)。
那么说明第 \(i + 2\) 步跳到的位置一定比第 \(i + 1\) 步的期望位置更优，此时我们也离最右端的火把远了一倍。

我们发现每跳两步会距离最右端的火把远一倍，所以最多跳 \(2 \log n + O(1)\) 步从 \(n\) 跳到 \(1\)。

Code(std)

#include <algorithm>
#include <vector>
#include "light.h"

using namespace std;
using LL = long long;

LL N = 1;
vector<LL> act = {1};

void prepare () {}

pair<LL, vector<LL>> solve (LL p) {
  vector<LL> ret = {N};
  LL x = N;
  while (x > 1) {
    x -= min(x - 1, N - x + 2);
    int i = upper_bound(act.begin(), act.end(), x) - act.begin() - 1;
    if (x - act[i] > p)
      x = act[i + 1];
    ret.insert(ret.begin(), x);
  }
  swap(ret, act);
  return {p, act};
}

pair<LL, vector<LL>> join (LL p) {
  N += p;
  return solve(p);
}

pair<LL, vector<LL>> leave (LL p) {
  N -= p;
  return solve(p);
}

Day1 T2 Bring Down the Grading Server (grading-server)

题意：Alice 和 Bob 两个人用电脑博弈，Alice 的电脑算力为 \(c_1\)，防火墙数为 \(f_1\)，Bob 的电脑有算力 \(c_2\)，防火墙数 \(f_2\)。
两个人轮流进行以下操作之一，第一个满足 \(c \le 0\) 的人负，以先手为例：

击破对方的一个防火墙，使 \(f_2\) 减小 \(1\)（\(f_2 = 0\) 时无法进行该操作）。

用自己的算力攻击对方的系统，使 \(c_2\) 减小 \(\max(c_1 - f_2S, 0)\)。

后手的操作同理。给定参数 \(S\)，进行 \(Q\) 次询问，每次给出 \(c_1, f_1, c_2, f_2\)，问 Alice 和 Bob 谁能赢，
令 \(N = \max(c_1, f_1, c_2, f_2)\)，保证 \(1 \le S \le 3 \times 10^4, 1 \le N \le 10^{12}, 1 \le Q \le 2.5 \times 10^5\)。

神秘题，先咕着。以后有时间再改。

Day1 T3 Brought Down the Grading Server? (balance)

题意：给定一个 \(N\) 行 \(S\) 列的矩阵，矩阵的值域为 \([1, T]\)，你可以对矩阵的每一列分别进行重排，使得对于任意一个数字，它在任意两列的出现次数之差不超过 \(1\)，你需要构造出方案。保证 \(S\) 可以表示为 \(2^k\)，其中 \(k\) 为正整数的形式。可以证明一定有解。
\(1 \le N, S, T \le 10^5, 1 \le NS \le 5 \times 10^5\)。

首先考虑 \(S = 2\) 的情况，那么题意就是有一个 \(N\) 行 \(2\) 列的矩阵，对于每一行可以选择是否 \(\text{swap}\)，使得对于每个数字，它在第一列和第二列出现次数之差不超过 \(1\)。

考虑建立图论模型，对于一行中两个数字 \((a, b)\)，我们在 \(a\) 和 \(b\) 之间连一条无向边，问题转化为将这个无向图定向，我们规定从左向右定向表示不交换，从右往左定向表示交换（或者根据数字大小决定，这个更加好写一些），我们要求所有点入度和出度之差不超过 \(1\)。

经典地转化为欧拉回路问题。建立超级源点 \(S\)，对于图上每个奇点向 \(S\) 连边，由于无向图的欧拉回路定向后，所有点入度和出度相等，所以补不超过一条边后所有点入度和出度之差不超过 \(1\)。

接下来考虑 \(S\) 为任意 \(2^k\) 的情况，我们可以分治解决，此时 \(2^k\) 给出了一个很好的性质——分治后得到一棵满二叉树，这说明任意时刻左右区间长度是相同的。

对于每一行，我们将左区间和右区间中的元素两两配对，类似的，这样做相当于刻画了一个限制：对于任意一个数字，它在左区间和右区间出现次数相同。我们一直分治做下去，直到到达了一个叶子结点。

并且我们可证明，只要我们保证，对于一个数，它在分治每一层满足左右区间出现次数之差不超过 \(1\)，那么任选两个分治树上的叶子，它的出现次数之差也不超过 \(1\)，这个是很好证明的：

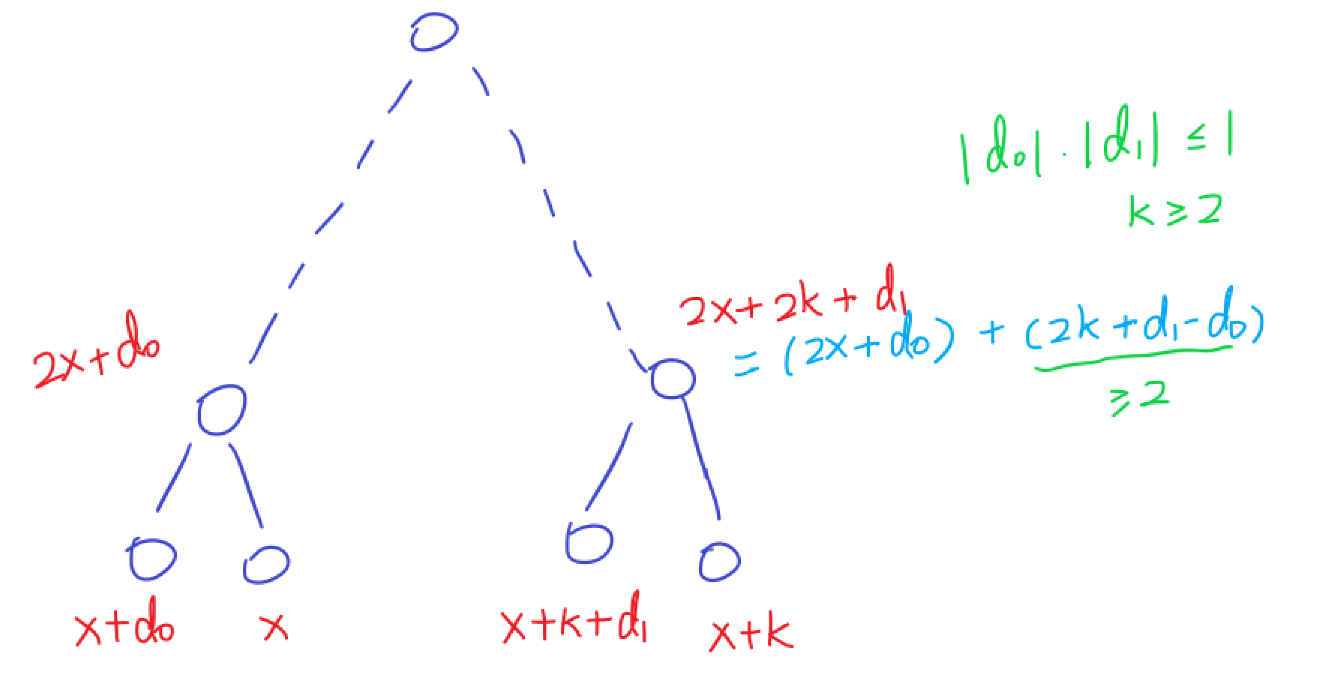
考虑反证，假设固定一个数字 \(v\)，在满二叉树上，称一个叶子的权值为这个数字在该处的出现次数，一个结点的子树大小为子树内所有叶子的权值和，那么存在任意两个叶子权值之差不小于 \(2\)，考虑设其中一个权值为 \(x\)，另一个权值为 \(x + k\)，其中 \(k \ge 2\)，我们只需证明一定存在二叉树上的一个结点，它的左右儿子子树大小之差不小于 \(2\)。
找出权值为 \(x\) 的结点的兄弟，权值设为 \(x + d_0\)，另一个结点的兄弟权值设为 \(x + k + d_1\)，注意到 \(|d_0|, |d_1| \le 1\)，否则在该处已经不合法。
接下来考虑它们父亲的权值，分别可以表示为 \(2x + d_0\) 和 \(2x + 2k + d_1\)，令 \(x' = 2x + d_0\)，\(k' = 2k + d_1 - d_0\)，那么两个父亲结点的权值可以表示为 \(x'\) 和 \(x' + k'\)，容易发现 \(k' \ge 2\)。
我们将原问题 \((x, x + k)\) 归约到了子问题 \((x', x' + k')\)，且子问题的限制不弱于原问题，考虑一直做下去直到找到 \(\text{LCA}\)，此时一定会出现不合法的情况。

时间复杂度 \(O(NS \log S)\)。

Code

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 1e5 + 5, M = 5e5 + 5; 

int n, s, t, E;
vector<int> v[N], ans[N], id[N];
vector<pair<int, int>> e[M];
vector<pair<int, int>>::iterator it[M];
int dir[M * 2];

void Dfs (int u, int la) {
  while (it[u] != e[u].end()) {
    pair<int, int> t = *it[u]++;
    int v = t.first, id = t.second;
    if (dir[id] != -1) continue; 
    dir[id] = (u < v);
    Dfs(v, id);
  }
}

void Solve (int l, int r) {
  if (l == r - 1) return;  
  int mid = (l + r) >> 1;
  vector<int> p; 
  for (int i = 1; i <= n; ++i) {
    for (int j = l; j < r; ++j) {
      p.push_back(v[i][j]);
    }
  }
  sort(p.begin(), p.end());
  p.resize(unique(p.begin(), p.end()) - p.begin());
  for (int i = 1; i <= n; ++i) {
    for (int j = l; j < r; ++j) {
      v[i][j] = lower_bound(p.begin(), p.end(), v[i][j]) - p.begin() + 1; 
    }
  }
  t = p.size(), E = 0; 
  fill(e + 1, e + t + 2, vector<pair<int, int>>());
  for (int i = 1; i <= n; ++i) {
    for (int j = l, k = mid; j < mid; ++j, ++k) {
      if (v[i][j] == v[i][k])
        id[i][j] = 0; 
      else {
        id[i][j] = ++E;
        e[v[i][j]].push_back({v[i][k], E});
        e[v[i][k]].push_back({v[i][j], E});
      }
    }
  }
  ++t;
  for (int i = 1; i < t; ++i) {
    if (e[i].size() & 1) {
      ++E;
      e[i].push_back({t, E});
      e[t].push_back({i, E});
    }
  }
  fill(dir + 1, dir + E + 1, -1);
  for (int i = 1; i <= t; ++i) {
    it[i] = e[i].begin();
  }
  for (int i = 1; i <= t; ++i) {
    if (it[i] != e[i].end())
      Dfs(i, 0);
  }
  for (int i = 1; i <= n; ++i) {
    for (int j = l, k = mid; j < mid; ++j, ++k) {
      if (id[i][j] && (dir[id[i][j]] ^ (v[i][j] < v[i][k])))
        swap(v[i][j], v[i][k]), swap(ans[i][j], ans[i][k]);
    }
  }
  Solve(l, mid), Solve(mid, r);
}

int main () {
  cin.tie(0)->sync_with_stdio(0);
  cin >> n >> s >> t;
  fill(v + 1, v + n + 1, vector<int>(s));
  fill(id + 1, id + n + 1, vector<int>(s));
  for (int i = 1; i <= n; ++i) {
    for (auto &x : v[i])
      cin >> x;
  }
  copy(v + 1, v + n + 1, ans + 1);
  Solve(0, s); 
  for (int i = 1; i <= n; ++i) {
    for (int j = 0; j < s; ++j) {
      cout << ans[i][j] << ' ';
    } 
    cout << '\n';
  }
  return 0;
}

Day2 T1 Tricks of the Trade (trade)

题意：给定一个序列两个长度为 \(n\) 的序列 \(a, b\)，你需要选一个长度至少为 \(k\) 的区间 \([l, r]\)，收益为区间中 \(b\) 的前 \(k\) 大值减去 \(a\) 的总和。求最大收益，并输出哪些位置可能在某一最优方案中成为 \(b\) 的前 \(k\) 大值。
\(1 \le n \le 2.5 \times 10^5, 1 \le a_i, b_i \le 10^9\)。

一道和这个很像的题目：JOISC2019 J - ケーキの貼り合わせ (Cake 3)。

我们定义一个区间的价值为 \(g(l, r) = f(l, r) - a_r + a_{l - 1}\)，其中 \(f(l, r)\) 表示序列 \(b\) 上区间 \([l, r]\) 中的前 \(k\) 大值之和，这里默认对 \(a\) 做了前缀和。那么第一问就是选一对 \(l, r\) 使得 \(g(l, r)\) 最大。

为了使用一些决策单调性技巧快速计算，我们需要证明 \(g(l, r)\) 满足四边形不等式，即对于任意 \(a \le b \le c \le d\)，有

\[g(a, c) + g(b, d) \ge g(a, d) + g(b, c) \]

由于 \(g\) 中 \(a\) 的部分可以被消掉，所以我们只需证明：

\[f(a, c) + f(b, d) \ge f(a, d) + f(b, c) \]

这个东西感觉挺显然的，你考虑无论前 \(k\) 大值在后一种方案中的分布位置如何，前一种方案都可以做一个一模一样的出来，所以前一种方案一定不劣。

然后第一问基本上就做完了，我们可以直接套路地分治做，然后对于一个区间地价值主席树即可维护。另一种方法是考虑莫队，有一个结论是你在决策单调性的分治树上，每次计算区间价值时直接移动端点，端点移动次数总和是 \(O(n \log n)\) 的，现在只需维护集合前 \(k\) 大值，平衡树或 \(\text{set}\) 即可。时间复杂度 \(O(n \log^2 n)\) 或 \(O(n \log n \log V)\)。

接下来考虑第二问怎么做，容易想到我们可以将所有价值最大的区间找出来，每一个形如 \((l, r, v)\)，表示有一种最优方案是选区间 \([l, r]\)，并且区间 \([l, r]\) 中第 \(k\) 大数为 \(v\)。对于区间 \([l, r]\) 中的某个 \(i\)，如果 \(b_i \ge v\) 那么它可能成为前 \(k\) 大值。

我们把一个 \((l, r, v)\) 看作一次区间 checkmin，考虑将所有最优区间按 \(v\) 从大到小排序，那么可以将区间 checkmin 变成区间赋值，我们只需最后遍历线段树做单点查询即可。

但是现在的问题是最优区间是 \(O(n^2)\) 级别的，直接找肯定不行。所以我们接下来考虑缩小最优区间的范围。

假设 \(a < b < c < d\)，且 \([b, c]\) 和 \([a, d]\) 都是最优区间，根据我们前面说明的四边形不等式，有 \([a, c], [b, d]\) 也是最优区间（考虑设最大价值为 \(w\)，\(g(a, c) + g(b, d) \ge g(b, c) + g(a, d) = 2w\)，且 \(g(a, c) \le w, g(b, d) \le w\)，则 \(g(a, c) = g(b, d) = w\)）。

并且考虑设一个区间 \([l, r]\) 的第 \(k\) 小值是 \(v_{l, r}\)，显然有 \(v_{a, c} \le v_{a, d}, v_{b, d} \le v_{a, d}\)，此时考虑用 \([a, c], [b, d]\) 两个区间替换 \([a, d]\) 一定不劣，所以这样包含另外一个最优区间的最优区间 \([a, d]\) 是“无用的”，我们可以直接忽略。

考虑对于每一个可能成为最优区间右端点的位置 \(i\)，找到最大的 \(p_i\) 满足 \([p_i, i]\) 是最优区间，这个在分治的时候控制一下取最大决策点即可，那么考虑上一个右端点 \(j\) 满足 \([p_j, j]\) 也是最优区间，只有区间 \([p_j, p_i]\) 内的左端点是“有用的”，否则它包含最优区间 \([p_j, j]\)。这样最优区间数就被缩减到了 \(O(n)\)。

时间复杂度 \(O(n \log^2 n)\) 或 \(O(n \log n \log V)\)。

Code

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
using LL = long long;

const int N = 2.5e5 + 5, M = 18;
const LL Inf = 1e18;

int n, k; 
LL a[N], f[N];
int b[N], rt[N], p[N];

struct S {
  int l, r, v;
}; 

namespace Seg {
  const int T = N * 32;
  const int V = 1e9;

  int tot, lc[T], rc[T], siz[T];
  LL sum[T];

  void Add (int &k, int t, int x, int L = 1, int R = V) {
    k = ++tot;
    siz[k] = siz[t] + 1;  
    sum[k] = sum[t] + x;
    if (L == R) return; 
    int mid = (L + R) >> 1;
    if (x <= mid) {
      rc[k] = rc[t];
      Add(lc[k], lc[t], x, L, mid);
    }
    else {
      lc[k] = lc[t];
      Add(rc[k], rc[t], x, mid + 1, R);
    }
  }

  LL Query (int lk, int rk, int x, int L = 1, int R = V) {
    if (L == R) return 1ll * x * L;
    int mid = (L + R) >> 1, rcnt = siz[rc[rk]] - siz[rc[lk]];
    if (x <= rcnt)
      return Query(rc[lk], rc[rk], x, mid + 1, R);
    else 
      return Query(lc[lk], lc[rk], x - rcnt, L, mid) + sum[rc[rk]] - sum[rc[lk]]; 
  }

  int Query2 (int lk, int rk, int x, int L = 1, int R = V) {
    if (L == R) return L; 
    int mid = (L + R) >> 1, rcnt = siz[rc[rk]] - siz[rc[lk]];
    if (x <= rcnt) 
      return Query2(rc[lk], rc[rk], x, mid + 1, R);
    else
      return Query2(lc[lk], lc[rk], x - rcnt, L, mid);
  }

  LL Query_kmax (int l, int r, int k) {
    return Query(rt[l - 1], rt[r], k);
  }

  int Query_kth (int l, int r, int k) {
    return Query2(rt[l - 1], rt[r], k);
  }
}

LL G (int l, int r) {
  return Seg::Query_kmax(l, r, k) - a[r] + a[l - 1];
}

void Solve (int l, int r, int L, int R) {
  if (l > r) return; 
  int mid = (l + r) >> 1, mp = L;
  LL mv = -Inf;
  for (int p = L; p <= min(mid - k + 1, R); ++p) {
    LL v = G(p, mid);
    if (v >= mv)
      mv = v, mp = p; 
  }
  f[mid] = mv, p[mid] = mp;
  Solve(l, mid - 1, L, mp);
  Solve(mid + 1, r, mp, R);
}

namespace Seg2 {
  #define lc (k << 1)
  #define rc ((k << 1) | 1)

  const int T = N * 4;
  int tag[T];

  void Build () {
    fill(tag, tag + (n * 4) + 1, -1);
  }

  void Node_assign (int k, int x) {
    tag[k] = x; 
  }

  void Pushdown (int k) {
    if (tag[k] != -1) {
      Node_assign(lc, tag[k]);
      Node_assign(rc, tag[k]);
      tag[k] = -1;
    }
  }

  void Assign (int k, int l, int r, int x, int L = 1, int R = n) {
    if (l <= L && r >= R) {
      Node_assign(k, x);
      return; 
    }
    Pushdown(k);
    int mid = (L + R) >> 1;
    if (l <= mid) {
      Assign(lc, l, r, x, L, mid);
    }
    if (r > mid) {
      Assign(rc, l, r, x, mid + 1, R);
    }
  }

  void Dfs (int k, int L = 1, int R = n) {
    if (L == R) {
      cout << (tag[k] != -1 && tag[k] <= b[L] ? '1' : '0'); 
      return; 
    }
    Pushdown(k);
    int mid = (L + R) >> 1;
    Dfs(lc, L, mid);
    Dfs(rc, mid + 1, R);
  }

  #undef lc 
  #undef rc
}

int main () {
  cin.tie(0)->sync_with_stdio(0);
  cin >> n >> k;
  for (int i = 1; i <= n; ++i) {
    cin >> a[i], a[i] += a[i - 1];
  }
  for (int i = 1; i <= n; ++i) { 
    cin >> b[i];
    Seg::Add(rt[i], rt[i - 1], b[i]);
  } 
  Solve(k, n, 1, n);
  LL ans = -Inf;
  for (int i = k; i <= n; ++i) {
    ans = max(ans, f[i]);
  }
  cout << ans << '\n';
  int la = 0; 
  vector<S> sv;
  for (int i = k; i <= n; ++i) {
    if (f[i] == ans) {
      int &j = p[i];
      for (int t = la; t <= j; ++t) {
        if (G(t, i) == ans)
          sv.push_back(S({t, i, Seg::Query_kth(t, i, k)}));
      } 
      la = j;
    }
  }
  auto cmp = [&](S a, S b) -> bool {
    return a.v > b.v;
  }; 
  sort(sv.begin(), sv.end(), cmp);
  Seg2::Build();
  for (auto s : sv) {
    Seg2::Assign(1, s.l, s.r, s.v);
  }
  Seg2::Dfs(1), cout << '\n';
  return 0; 
}

Day2 T2 The Ties That Guide Us (incursion)

题意：给定一棵树 \(n\) 个结点的树 \(T_1\) 和一个 \(T_1\) 上的关键点 \(safe\)，你需要给每一个点 \(i\) 标一个权值 \(v_i\)，需要满足 \(0 \le v_i < v_{\max}\)。
现在将 \(T_1\) 任意重标号得到 \(T_2\)，再将 \(T_2\) 的形态给你，并且你一个点 \(u\) 和 \(u\) 的权值，你需要从 \(u\) 走到 \(T_2\) 上与 \(safe\) 对应的点 \(\hat{safe}\)，你每次可以将 \(u\) 移动到一个与 \(u\) 相邻的点，并且得到这个相邻点的权值，要求访问的点数不超过 \(\text{dist}(u, safe) + 30\)，可以在任意时刻到达 \(safe\) 并结束程序。
\(n \le 4.5 \times 10^4, v_{\max} \ge 2\)。保证 \(T_1\) 和 \(T_2\) 上每个点度数 \(\le 3\)。

\(v_{\max} = 2\) 的情况，实际上就是只能对点进行 \(01\) 染色。

首先我们做一些观察：发现无用的移动（远离 \(\hat{safe}\)）最多只能有 \(15\) 次，而这个 \(15\) 很容易使我们联想到 \(\log n\)。

考虑一个弱化版本：假设我们知道 \(T_1\) 与 \(T_2\) 的某个点有对应关系，记其在 \(T_1\) 上编号为 \(r\)，考虑以 \(r\) 为根，做如下染色：

在 \(safe\) 到 \(r\) 的路径上染色成 \(1\)，其他点染色成 \(0\)。

考虑在 \(T_2\) 上还是钦定 \(r\) 的对应点为根，你以某一点作为起点，先不断向上跳，跳到一个颜色为 \(1\) 的点，然后再向下跳，尝试每个儿子，如果是 \(1\) 就递归到这个儿子继续向下跳，直到每个儿子都是 \(0\)，此时当前所在的点就是 \(\hat{safe}\)。

跳儿子的过程可以考虑重链剖分优化，每次先跳重儿子，由于轻边的个数是 \(\log n\)，并且除根以外每个点至多两个儿子，所以错误移动次数大致是 \(\log n\) 的。

现在考虑如何找对应点，下面我们讲解两种方法。

第一种是我和大多数选手的做法，考虑套用我们在做树的同构的时候，将无根树变成有根树的方法，那就是直接钦定重心为根。

如果重心是一个，那就是前面的情况，直接做完了。但如果有两个重心就会出现问题。

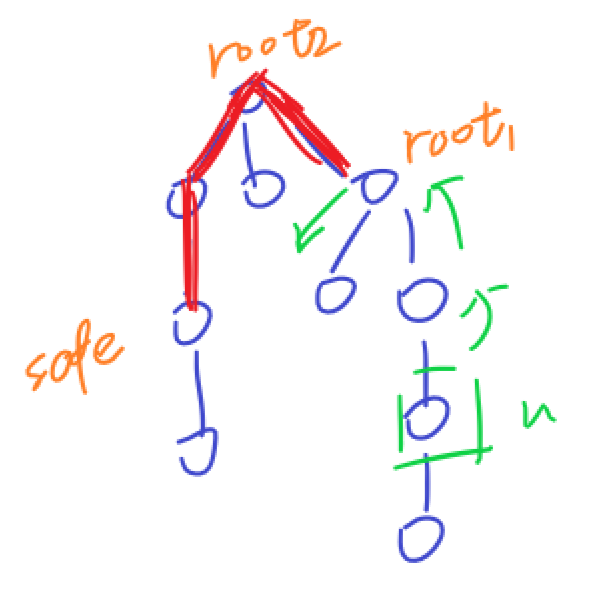
考虑如上情况，假设我们在 \(T_1\) 上找重心找到了 \(root_1\)，于是我们将 \(safe\) 到 \(root_1\) 的路径权值设为 \(1\)（图上标红），然后你在 \(T_2\) 上找的重心是 \(root_2\)，从 \(u\) 开始走，注意到你走到 \(root_1\) 就会向下跳，那么你就寄了。

当然可以大力分讨一下，试着将两个重心染成不同颜色。但是这样很麻烦，而且不够优雅。

正解其实很简单，只要在 \(T_1\) 上选重心时选靠近 \(safe\) 的就行，记为 \(root_1\)，另一个重心记为 \(root_2\)，这样考虑割掉两个重心之间的边，将一棵树划分成两个点集，选靠近 \(safe\) 的重心为根相当于保证 \(root_1\) 和 \(safe\) 在一个点集中。此时如果 \(u\) 和 \(root_1\) 在一个点集中，那么它和 \(root_2\) 永远不会相遇，这当然是正确的。否则由于 \(safe\) 和 \(root_1\) 在同一点集，那么容易 \(root_2\) 所在点集中所有点不会被染成 \(1\)，并且 \(root_1\) 是 \(root_2\) 的父亲，所以从 \(u\) 跳到 \(root_2\) 后会继续跳到 \(root_1\)，这样也是正确的。

第二种做法来自 CEOI 官方题解，考虑拉出任意一条直径，取它的中点作为根。可以证明，能够成为直径中点的点不超过 \(2\) 个（考虑反证，如果超过两个的话尝试两两配对，可以得到一条更长的直径）。

这个做法也存在直径中点不唯一，无法区分的情况，解决方法也是一样的，钦定离 \(safe\) 近的那个直径中点作为根就行了。

Code(std)

#include <bits/stdc++.h>
#include "incursion.h"
using namespace std;

int n;
vector<vector<int>> adj;
vector<int> parent;
vector<int> depth;
vector<int> subtree_size;

int visit (int v);

void dfs (int from, int d = 0) {
  depth[from] = d;
  for (int j : adj[from]) {
    if (j == parent[from]) continue;
    parent[j] = from;
    dfs(j, d + 1);
    subtree_size[from] += subtree_size[j];
  }
}

int find_center (int treasure_pos) {
  parent.assign(n, -1);
  depth.assign(n, -1);
  subtree_size.assign(n, 0);

  dfs(treasure_pos);
  int end1 = 0;
  for (int i = 1; i < n; ++i)
    if (depth[i] > depth[end1]) end1 = i;

  parent[end1] = -1;
  dfs(end1);
  int end2 = 0;
  for (int i = 1; i < n; ++i)
    if (depth[i] > depth[end2]) end2 = i;

  int center = end2;
  while (depth[center] * 2 > depth[end2] + 1) center = parent[center];

  subtree_size.assign(n, 1);
  parent[center] = -1;
  dfs(center);
  return center;
}

void to_adj_list (const vector<pair<int, int>>& edges) {
  n = edges.size() + 1;
  adj.assign(n, {});
  for (auto [a, b] : edges) {
    --a;
    --b;
    adj[a].push_back(b);
    adj[b].push_back(a);
  }
}

vector<int> mark (vector<pair<int, int>> F, int safe) {
  --safe;
  to_adj_list(F);
  find_center(safe);
  vector<int> ties(n, 0);
  do {
    ties[safe] = 1;
    safe = parent[safe];
  } while (safe != -1);
  return ties;
}

void locate (vector<pair<int, int>> F, int curr, int t) {
  --curr;
  to_adj_list(F);
  find_center(0);
  while (t == 0 && parent[curr] != -1) {
    curr = parent[curr];
    assert(curr != -1);
    t = visit(curr + 1);
  }
  for (;;) {
    sort(adj[curr].begin(), adj[curr].end(), [&](int a, int b) { return subtree_size[a] > subtree_size[b]; });
    bool found = false;
    for (int j : adj[curr]) {
      if (j == parent[curr]) continue;
      t = visit(j + 1);
      if (t) {
        found = true;
        curr = j;
        break;
      }
      t = visit(curr + 1);
    }
    if (!found) return;
  }
}

Day2 T3 How to Avoid Disqualification in 75 Easy Steps (avoid)

可能另一个较为著名的形式是 ZROI 2779（正睿 2023 NOIP 赛前 20 天冲刺集训 Day13 T4），下面以该版本进行讲解。

题意：有两个隐藏的数字 \(a, b\)，保证 \(1 \le a, b \le N\)。你需要构造一系列询问，每次询问包含一个数字集合，你可以知道 \(a, b\) 中是否存在至少一个数在集合。你需要确保你可以通过这些询问找到这个无序对 \((a, b)\)，需要保证询问次数 \(m \le m_{\max}\)。
\(N = 1000, m_{\max} \ge 26\)。

容易发现题意等价于构造 \(N = 1000\) 个不超过 \(m_{\max}\) 位的二进制数 \(x_1, x_2, \ldots, x_N\)，满足任意选两个 \((a, b)\) 满足 \(a \le b\)，得到的 \(x_a \ \text{OR} \ x_b\) 不同，其中 \(\text{OR}\) 表示按位或运算。

这道题目非常有意思，在 2023 年由 xtq 从 CEOI 搬到 ZROI 给我们考，然后 xtq 放了一个假的做法在题解区，我们一整个机房对着研究了一个下午，最多只能达到 \(N = 930\)，于是大家都放弃了，后来打开 xtq 的 std 发现他的也过不了，最后他唱歌谢罪了。

下面是该题目的若干做法：

Solution 1

直接嗯做，每次随一个数放到最后面，写的好看大概能过 \(m = [28, 30]\)，加一些奇奇怪怪的优化，比如 \(\text{popcount}\) 不在某个合理的范围内肯定是不优的，大概可以过 \(m = 27\)，这是赛时我们大多数人的做法。

Solution 2

该做法就是 xtq 在原题解中的做法（后来换了），其实这个做法是比较优的，但是距离 AC 可能还差一点。然后被我们喷的理由是，题解最后有一句“很简单啊！”。真是简简又单单了。

讲一下具体怎么做，你考虑一次性加入所有数的话，可能有一些数在一开始就是比较劣的，然后它就会一直影响整个方案。

所以我们可以先对于 \(m = 21/22\) 做随机加数，直到加不动了为止（在实现上可以刻画为连续随机 \(Cnt\) 个数全部加入失败，其中 \(Cnt\) 为设定的某一参数），这时我们新开一个位，为当前的所有数在这一位补一个 \(0/1\)，其中你可以设一个合适的 \(0\) 与 \(1\) 的比例。这样一个很劣的数它的影响就会减少。

考虑为这个做法拼上前面 \(\text{popcount}\) 的优化，在 \(m = 26\) 时大概可以做到 \(N = 700\)。

接下来就是我们机房发挥人类智慧的时候了。下面是若干可能的优化方法：

考虑记录每个数和其他数冲突的次数，如果一个数和其他数冲突次数很多，我们就认为它肯定不优，对于这样的数随机删除一些。
用双端队列维护当前所有的数，如果卡壳了就随机 pop 掉前面的若干个数。
在加位的时候不是要补 \(0/1\) 吗，考虑这个时候定比例可能不合适，考虑稍微搜索或者三分一下，把最优的那个拿出来继续做。
不是可以加位吗？那为什么不能删位呢？也是考虑随机删掉一位看看优不优之类的，或者随机对某一位重构。

还有很多做法，反正我们每人都写了一堆玄学优化然后拼起来，最优秀的是 hjc 的，他在 \(m = 26\) 时达到了 \(N = 930\)，但是还是没有过。

Solution 3

CEOI 的官方题解是模拟退火，但是我们机房都不太相信模拟退火，所以这个送给大家自己研究。

Solution 4

这个是 maoyiting 的做法和 xtq 后来补上去的新题解。

这个做法代码实现上很简单，大概就是固定 \(\text{popcount} = 8\)，然后强制两两 \(\text{OR}\) 起来 \(\text{popcount} > 10/11\)，但是我们机房的人并不知道为什么这样限制可以过，感觉也是枚举出来的结果。

标签：le,int,火把,safe,CEOI2023,区间,考虑
From： https://www.cnblogs.com/hztmax0/p/18394906

CEOI2023