cf_补题计划_Edu_163_DE

D. Tandem Repeats?
呃

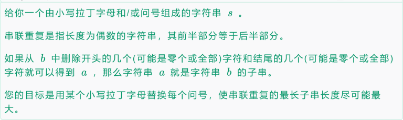
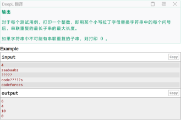
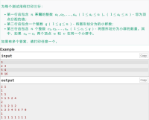
从复杂度来说，可以进行\(n^2\)的操作，呃因为是子串数量级也是\(n^2\),考虑是否子串之间可以相互转移，这个很类似求最长回文串(对于最长回文串我们枚举中点,向外延申即可，因为对于同一个中心可以转移)，而对于串联重复串，前一部分等于后一部分，我们可以考虑固定长度，那么长度一样的字串就可以转移。

跟回文串的处理差不多

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pb push_back
#define pii pair<int, int>
#define all(a) a.begin(), a.end()
#define debug(x) cout << #x << " = " << x << endl
#define sz(a) ((int)a.size())
const int mod = 998244353, N = 505, G = 3;
void solve()
{
    ll ans = 0, n;
    string a;
    cin >> a;
    n = a.length();
    a = ' ' + a;
    for (ll k = n; k >=1; k--)
    {
        ll sum = 0;
        for (int i = 1; i + k <= n; i++)
        {
            if (a[i] == a[i + k] || a[i] == '?' || a[i + k] == '?')//如果相等就+1
                sum++;
            else
                sum = 0;
            if (sum >= k){
                cout << k * 2 << endl;
                return;
            }
        }
    }
    cout << 0 << endl;
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

E. Clique Partition

呃，大概意思是将n个数，每个数给个数，然后在把他们分成m块，每块里面满足\(|i-j|+|a_i-a_j|<=k\)，然后让m尽可能的小。

然后我们发现i,j尽量的越接近会让|i-j|+|a_i-a_j|更小，更容易满足小于等于k的要求，所以每块的选取应该是连续的，然后大力guess

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pb push_back
#define pii pair<int, int>
#define all(a) a.begin(), a.end()
#define debug(x) cout << #x << " = " << x << endl
#define sz(a) ((int)a.size())
const int mod = 998244353, N = 2e5 + 10, G = 3;
ll d[N], c[N];
void solve()
{
    ll n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
        d[i] = 0;
    for (int i = 1; i <= n; i++)
    {
        c[i] = (i - 1) / k + 1;
        d[c[i]]++;
    }
    ll sum = 0;
    for (int i = 1; i <= n; i++)
    {
        if (c[i] != c[i - 1])
            sum = 0;
        sum++;
        if (sum <= d[c[i]] / 2)
            cout << (c[i] - 1) * 2 * k + 1 + d[c[i]] / 2 - i << ' ';
        else
            cout << (c[i] - 1) * 2 * k + 1 + d[c[i]] / 2 + d[c[i]] - i << ' ';
    }
    cout << endl;
    cout << (n - 1) / k + 1 << endl;
    for (int i = 1; i <= n; i++)
        cout << c[i] << ' ';
    cout << endl;
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}