Develop

题目链接：luogu AGC035E

题目大意

一开始有 -1e18~1e18 的所有整数，然后你每次操作可以在 1~N 中选一个还在的数 x，擦掉他，然后查看 x-2,x+K，如果没有就把数加上。
然后问你你操作若干次之后，剩下的数有多少中情况。

思路

考虑先把有跟没有互换。
然后发现如果我们要 \(x,x-2\) 同时都出现，那我们一定要先弄 \(x\)，再弄 \(x-2\)，不然会把 \(x-2\) 擦掉。

然后对于这个关系我们建一条边 \(x\rightarrow x-2\)，同理有 \(x\rightarrow x+k\)。
那也就是说我们要选一些点集，使得不存在环。
（因为只有是 DAG 你才能安排出顺序）

然后我们按 \(k\) 的奇偶性进行讨论。
如果 \(k\) 是偶数，那形成的环就是 \(x,x+2,...,x+k,x\) 这样的。
那就是我们把位置奇偶分别做一次，就不能出现连续的 \(k/2\) 个都选你的情况，直接 \(f_{i,j}\) 前 \(i\) 个位置，最后选了连续的 \(j\) 个的情况，直接 DP 即可。

如果 \(k\) 是奇数，那考虑环是什么样的。
会发现可以形如在偶数的下标跳若干个 \(2\)，然后跳一下 \(k\)，在奇数的部分跳一段 \(2\)，再跳 \(k\)。

（盗用一张图就是这样的：）

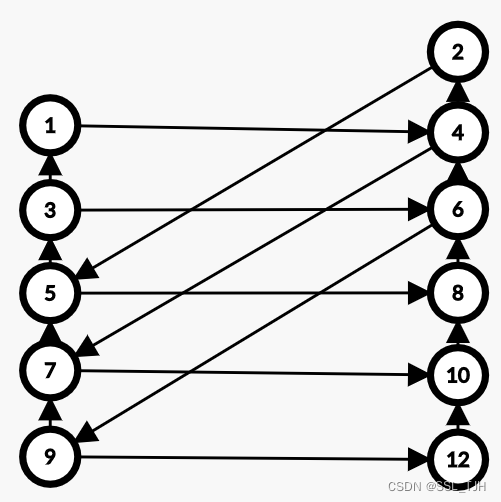
然后你把 \(x,x+k\) 分在同一层，那我们可以理解为一个环是这样的一条路径：
往上，往右，往上。
然后两次往上的和 \(k+1\)，也就是总共的长度是 \(k+1\)。
那你也可以 DP，设 \(f_{i,j,k}\) 为前 \(i\) 层当前的路径长度是 \(j\)，右边一条值的路径的长度是 \(k\)。

然后转移一下即可。

代码

#include<cstdio>
#include<iostream>
#define ll long long

using namespace std;

const int N = 155; 
int n, K;
ll mo, f[N][N], g[N << 1][N][N];

void slove1() {
	f[0][0] = 1;
	for (int i = 0; i < n; i++)
		for (int j = 0; j <= K / 2; j++) {
			if (!f[i][j]) continue;
			if (j + 1 <= K / 2) (f[i + 1][j + 1] += f[i][j]) %= mo;
			(f[i + 1][0] += f[i][j]) %= mo;
		}
	ll ans1 = 0, ans2 = 0;
	for (int i = 0; i <= K / 2; i++) (ans1 += f[n / 2][i]) %= mo, (ans2 += f[(n + 1) / 2][i]) %= mo;
	printf("%lld", ans1 * ans2 % mo);
}

//i - i+K
void slove2() {
	g[0][0][0] = 1; int nxt = 0;
	for (int i = 0; i < n + K - 1; i += 2) { nxt = i + 2;
		for (int j = 0; j <= K + 1; j++)
			for (int k = 0; k <= n; k++)
				(g[i + 2][0][0] += g[i][j][k]) %= mo;
		if (i + 2 <= n) {
			for (int j = 0; j <= K + 1; j++)
				for (int k = 0; k <= n; k++)
					(g[i + 2][0][k + 1] += g[i][j][k]) %= mo;
		}
		if (i + 2 >= 1 + K) {
			for (int j = 1; j < K + 1; j++)
				for (int k = 0; k <= n; k++)
					(g[i + 2][j + 1][0] += g[i][j][k]) %= mo;
			for (int k = 0; k <= n; k++)
				(g[i + 2][0][0] += g[i][0][k]) %= mo;//1 0
		}
		if (i + 2 <= n && i + 2 >= 1 + K) {
			for (int j = 0; j < K + 1; j++) {
				for (int k = 0; k < n && k < K; k++) {
					(g[i + 2][max(k + 2, j + 1)][k + 1] += g[i][j][k]) %= mo;
				}
			}
		}
	}
	ll ans = 0;
	for (int j = 0; j <= K + 1; j++)
		for (int k = 0; k <= n; k++)
			(ans += g[nxt][j][k]) %= mo;
	printf("%lld", ans);
}

int main() {
	scanf("%d %d %lld", &n, &K, &mo);
	
	if (K & 1) slove2();
		else slove1();
	
	return 0;
}