题解:P10358 [PA2024] Obrazy
题目传送门
即当最小的画框都不可能覆盖整个矩形墙面时,输出 −1。
[PA2024] Obrazy
题目背景
PA 2024 3C
题目描述
题目译自 PA 2024 Runda 3 Obrazy,感谢 Macaronlin 提供翻译
给定尺寸为 $h\times w$ 的矩形墙面,以及 $n$ 种尺寸的正方形画框,每种尺寸画框都有无穷多个。对于任意两种不同尺寸的画框,其中一个尺寸的边长总能整除另一个尺寸的边长。
现用这些画框完全覆盖墙面,而且画框之间不能重叠,只能边缘相接,请求出最少需要购买多少个画框?如果不可能完全覆盖墙面,则程序应输出 $-1$。
输入格式
第一行两个整数 $h$ 和 $w\ (1\le h,w\le 10^9)$,表示墙面大小。
第二行一个整数 $n\ (1\le n\le 30)$,表示画框个数。
第三行 $n$ 个整数 $d_1,d_2,\ldots,d_n\ (1\le d_i\le 10^9,d_i<d_{i+1})$,表示每个正方形画框的大小,保证 $d_{i+1}$ 能被 $d_i$ 整除。
输出格式
输出一行一个整数,如果可以完全覆盖墙面,输出最少要购买多少画框,否则输出 $-1$。
样例 #1
样例输入 #1
6 10
3
1 3 6
样例输出 #1
9
样例 #2
样例输入 #2
3 3
1
2
样例输出 #2
-1
提示
在第一个样例中,Byteasar 可以用九个画框(六个 $1\times 1$、两个 $3\times 3$ 和一个 $6\times 6$)覆盖一面墙,具体如下:
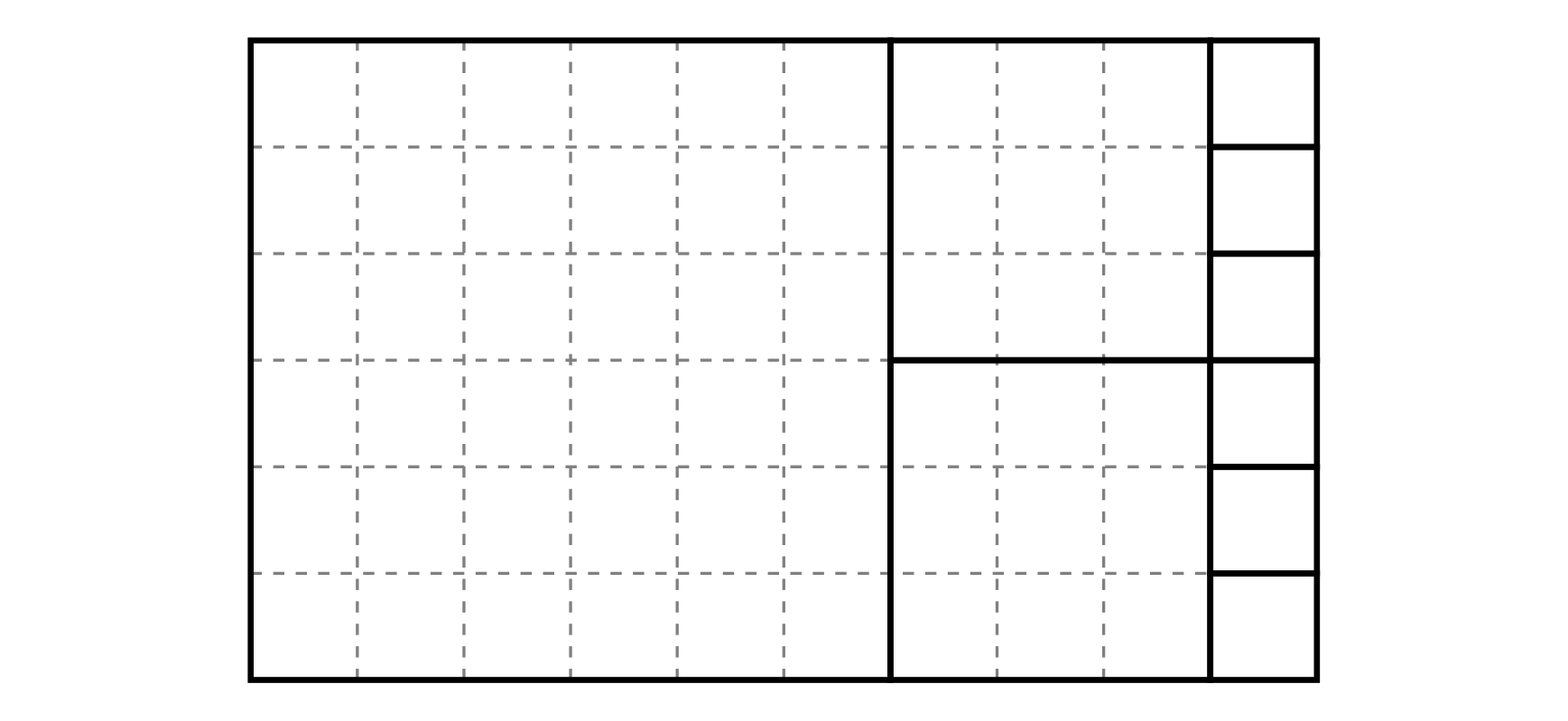
在第二个样例中,无法完全覆盖墙面。
--------------------分割线--------------------
意思
用最少的方块贴最大的墙,无遗漏重叠。
过程
我们先看图

特判
因为其中一个尺寸的边长总能整除另一个尺寸的边长。
也就是说,只要连最小的方块都不能整除(正好铺满)边长,就输出 -1 。
否则用大的尽量替换小的
怎么说呢,建议降橙。
代码不重要,主要是思路
#include <bits/stdc++.h>
using namespace std;
const int N = 35;
long long h, w, n, d[N], ans;
int main(){
cin >> h >> w >> n;
for(int i = 1; i <= n; i++) cin >> d[i];
if((h % d[1]) || (w % d[1])){
cout << -1;
return 0;
}
ans = h / d[1] * w / d[1];
for(int i = 2; i <= n; i++) ans -= (((d[i] / d[i - 1]) * (d[i] / d[i - 1]) - 1) * (h / d[i]) * (w / d[i]));
cout << ans;
return 0;
}