首页 > 其他分享 >数据结构（二）- 线性表

数据结构（二）- 线性表

时间：2024-08-19 15:06:12浏览次数：10  
标签：线性表 int 元素 list 指针 printf 数据结构 linear

数据结构（二）- 线性表

数据结构三要素——逻辑结构、数据的运算、存储结构；

存储结构不同运算实现的方式不同；

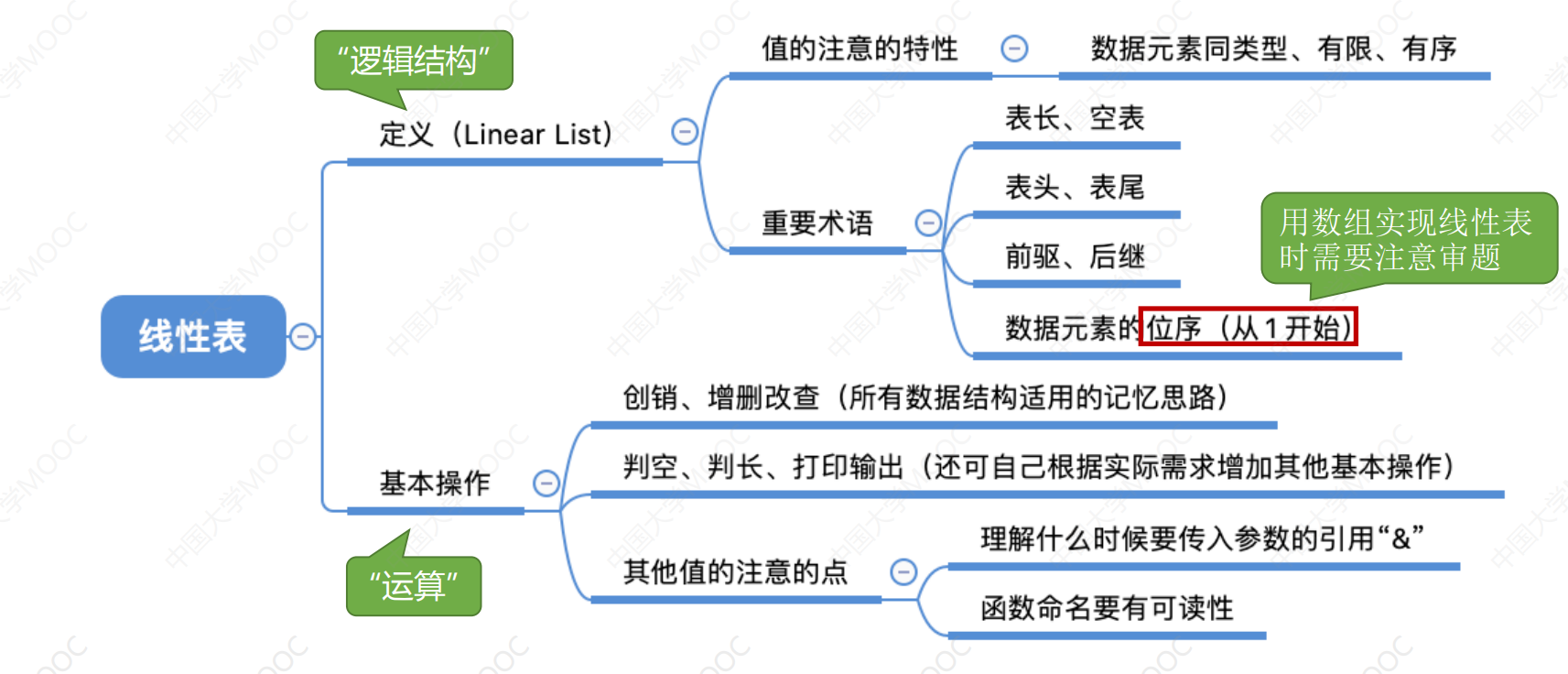
image-20240814181910728

1. 线性表的定义

image-20240814180242739

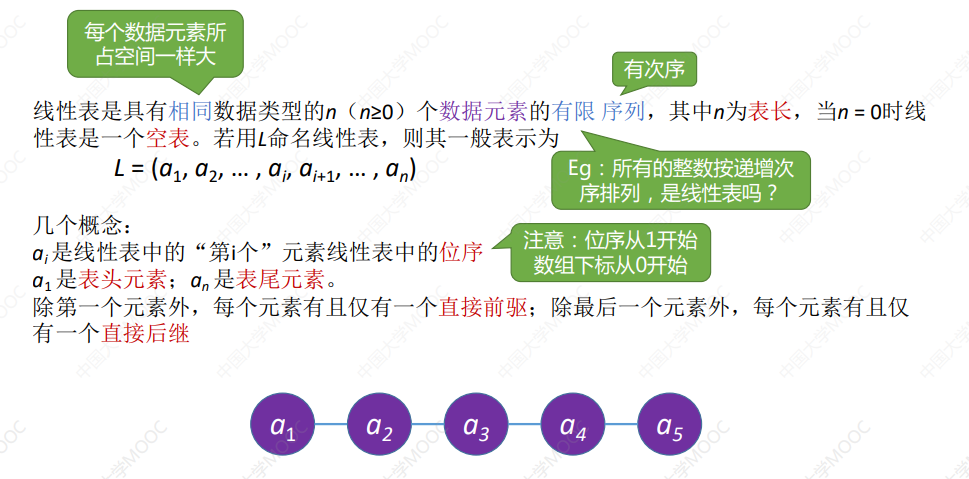
定义：线性表是具有相同数据类型的 n(n>0) 个数据元素的有限序列，其中 n 为表长，当n=0线性表是一个空表。一般表示为

L = (a1, a2, … , ai, ai+1, … , an)
// 位序从 1 开始, 数组下标从 0 开始;

image-20240814180605175

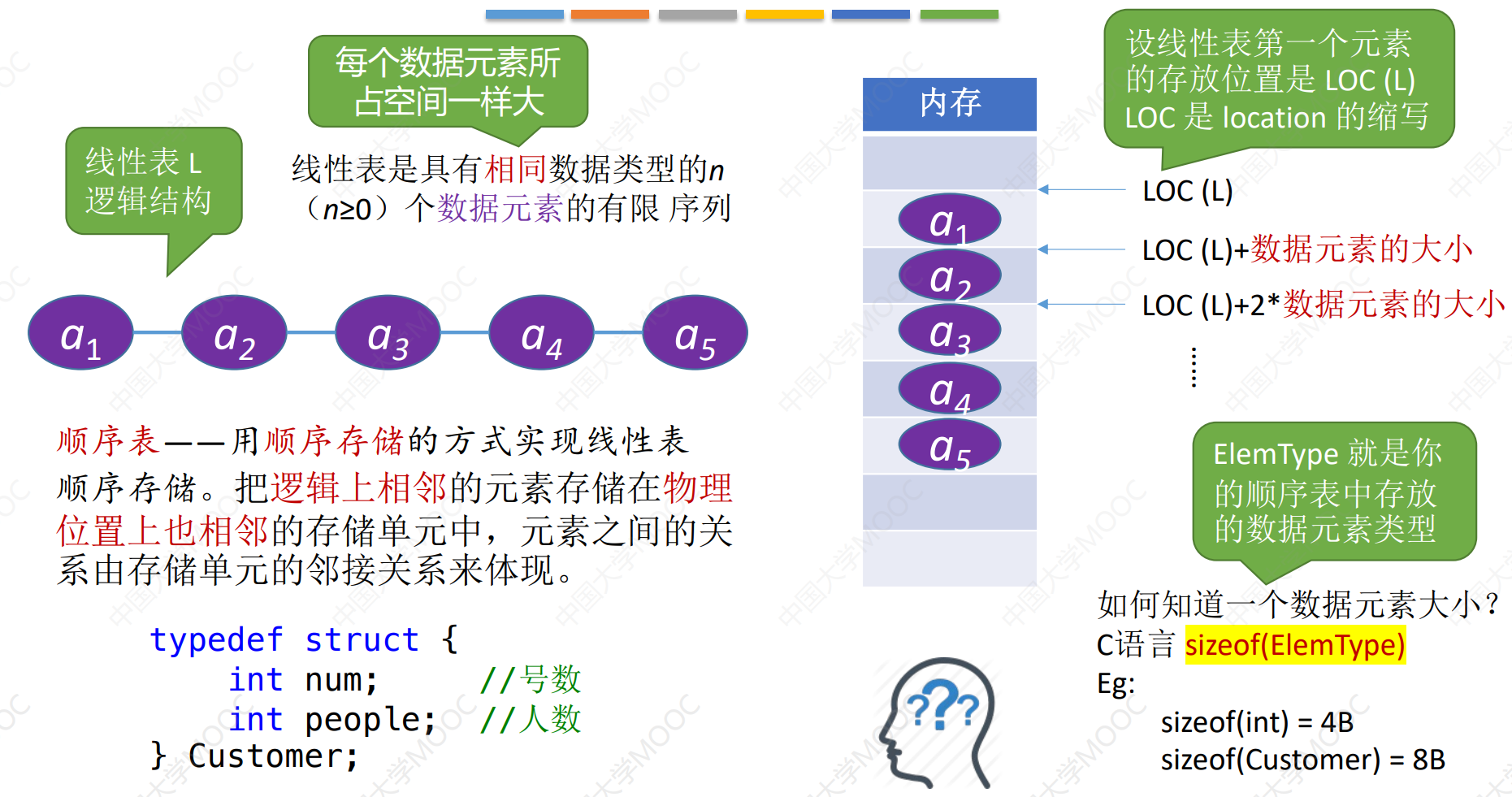
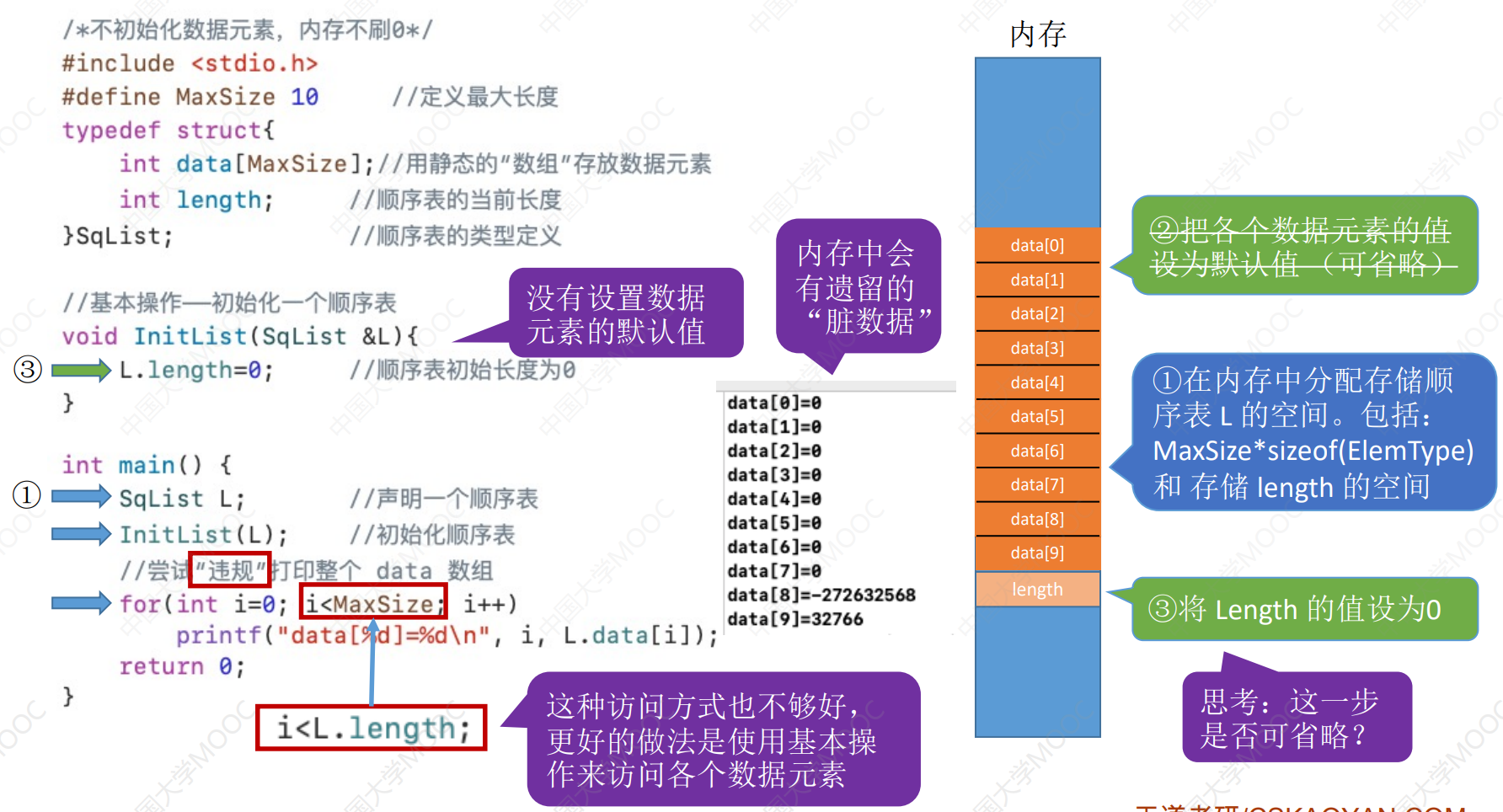
顺序表：用顺序存储的方式实现线性表 顺序存储。把逻辑上相邻的元素存储在物理 位置上也相邻的存储单元中，元素之间的关 系由存储单元的邻接关系来体现

image-20240814182212852

初始化相关的元素

声明相关的结构体与函数，在common.h声明变量和常量；

// common.h
// Created by 86152 on 2024/8/14.
//

#ifndef PRO_LINEAR_LIST_COMMON_H
#define PRO_LINEAR_LIST_COMMON_H

#include <stdlib.h>
#include <stdio.h>

#define MaxSize 10  // define 后面不需要加分号;

typedef struct SqList {
    int data[MaxSize];  // 使用静态数组存放数据元素;
    int length;  // 顺序表的当前长度
} SqList, *L;  // 顺序表类型的定义
void InitList(L L);

#endif //PRO_LINEAR_LIST_COMMON_H

初始化线性表的函数；

// linear_list.c 
// Created by 86152 on 2024/8/14.
//
#include "common.h"

/// 初始化线性表;
/// \param L 线性表结构体指针;
void InitList(L L) {
    for (int i = 0; i < MaxSize; i++) {
        L->data[i] = 0;  // 初始化将元素初始化为 0 
        L->length = 0;
    }
}

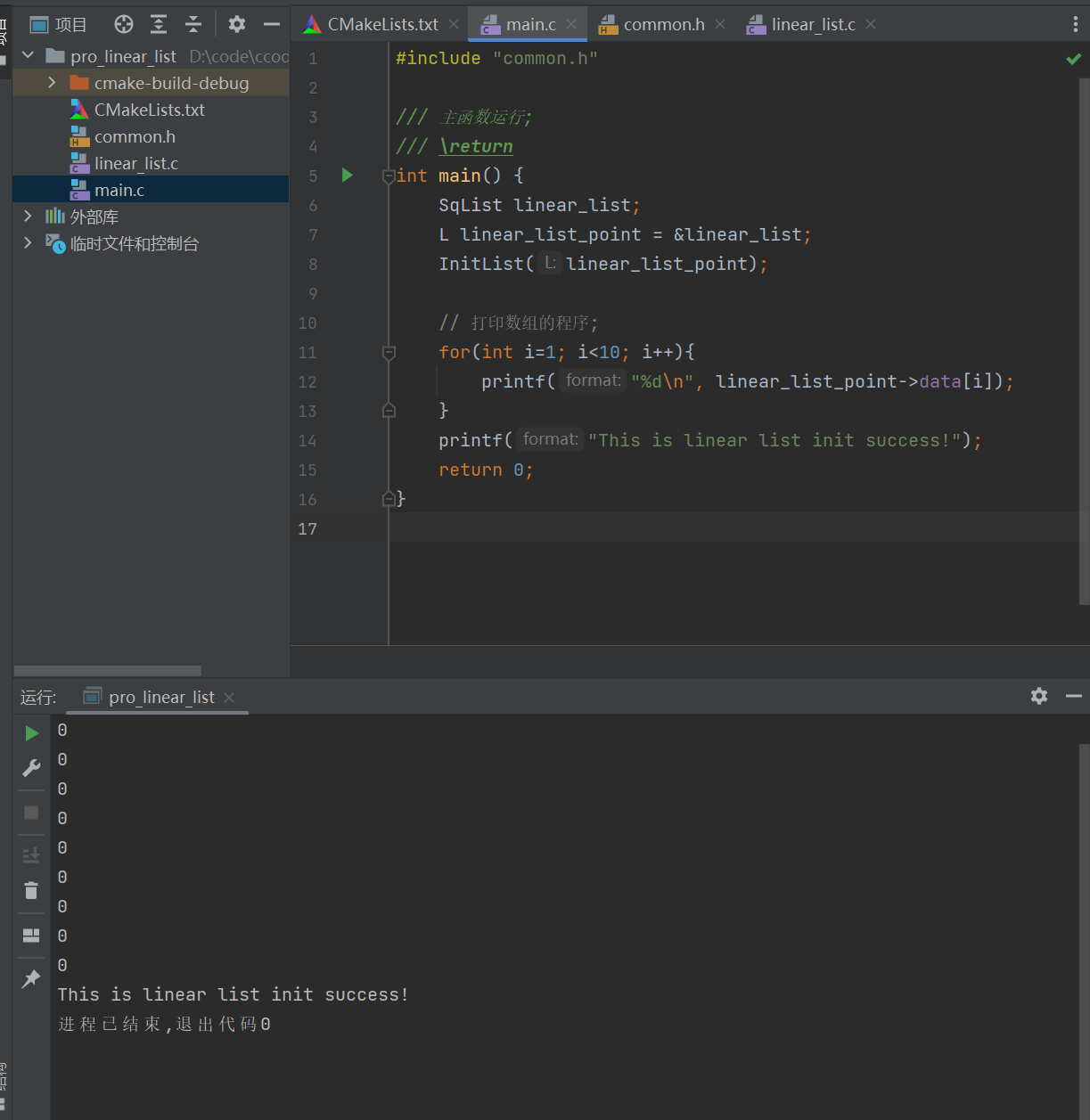
主函数运行

// main.c 
#include "common.h"

/// 主函数运行;
/// \return
int main() {
    SqList linear_list;
    L linear_list_point = &linear_list;
    InitList(linear_list_point);

    // 打印数组的程序;
    for(int i=1; i<10; i++){
        printf("%d\n", linear_list_point->data[i]);
    }
    printf("This is linear list init success!");
    return 0;
}

image-20240814205847329

image-20240814212714570

补充：

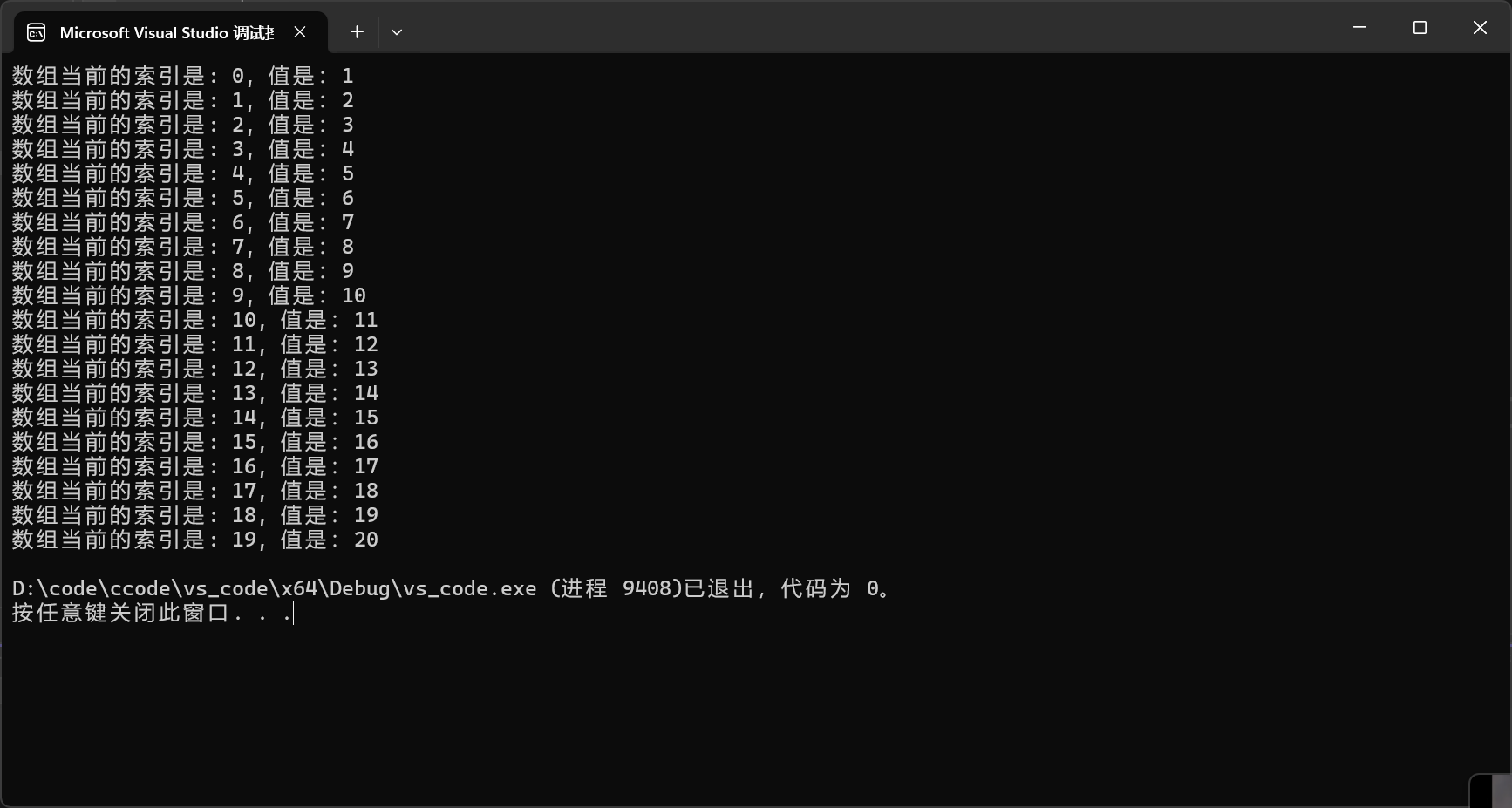
void define_arr(int len) {
	// 定义并打印指定长度的数组;
	int* arr = (int*)malloc(len * sizeof(int));  // 使用 malloc 申请内存空间, 在强制转换成为整形的指针类型;
	if (arr == NULL) {
		// 分配内存之后, 检查返回值是否是 NULL ， malloc 函数执行失败返回值是 NULL
		printf("Memory allocation failed\n");
		printf("内存分配失败！\n");
	}

	// 数组是连续的内存位置, 因此不需要进行数组的定义;
	for (int i = 0; i < len; i++) {
		// 向数组中循环插入元素;
		arr[i] = i+1;
	}

	// 打印结果数组;
	for (int i = 0; i < len; i++) {
		printf("数组当前的索引是: %d, 值是：%d\n", i, arr[i]);
	}

	// 使用完成之后, 释放内存;
	free(arr);
	arr = NULL; // 将指针设置成为 NULL ， 避免指针成为悬垂指针

}

int main() {
    define_arr(20);
    return 0;
}

image-20240819110942498

悬垂指针（Dangling Pointer）是指一个指针变量，它指向的内存已经被释放或者不再有效，但指针本身仍然保留了之前指向的内存地址。由于该内存区域可能已经被操作系统回收并分配给其他用途，继续使用悬垂指针访问或修改该内存区域将导致未定义行为，可能引发程序崩溃或数据损坏。

悬垂指针的常见情况包括：

  1. 释放内存后未清零：在使用 free 释放动态分配的内存后，如果没有将指针设置为 NULL，指针仍然指向之前分配的内存地址，此时该指针就成为了悬垂指针。
  2. 函数返回局部变量的地址：如果一个函数返回其局部变量的地址，一旦函数执行完毕，局部变量的生命周期结束，其内存可能被回收，此时返回的地址指向的就是一个悬垂指针。
  3. 使用已经被释放的内存：在内存被 free 释放后，如果再次使用这块内存（例如通过之前保存的指针），那么这个指针就是悬垂的。
  4. 对象生命周期结束：在某些编程语言中，对象可能在特定时间点被自动销毁。如果在此之后仍然持有对象的引用或指针，那么这个引用或指针就是悬垂的。

为了避免悬垂指针，可以采取以下措施：

  • 在释放内存后立即将指针设置为 NULL。
  • 避免返回局部变量的地址，可以使用动态分配的内存或引用传递。
  • 使用智能指针（如 C++ 中的 std::unique_ptr 或 std::shared_ptr）来自动管理内存，它们在适当的时候会自动释放内存并防止悬垂指针的产生。
  • 确保在对象生命周期结束后不再使用其引用或指针。

悬垂指针是编程中常见的错误之一，正确管理内存和指针是编写健壮程序的关键。

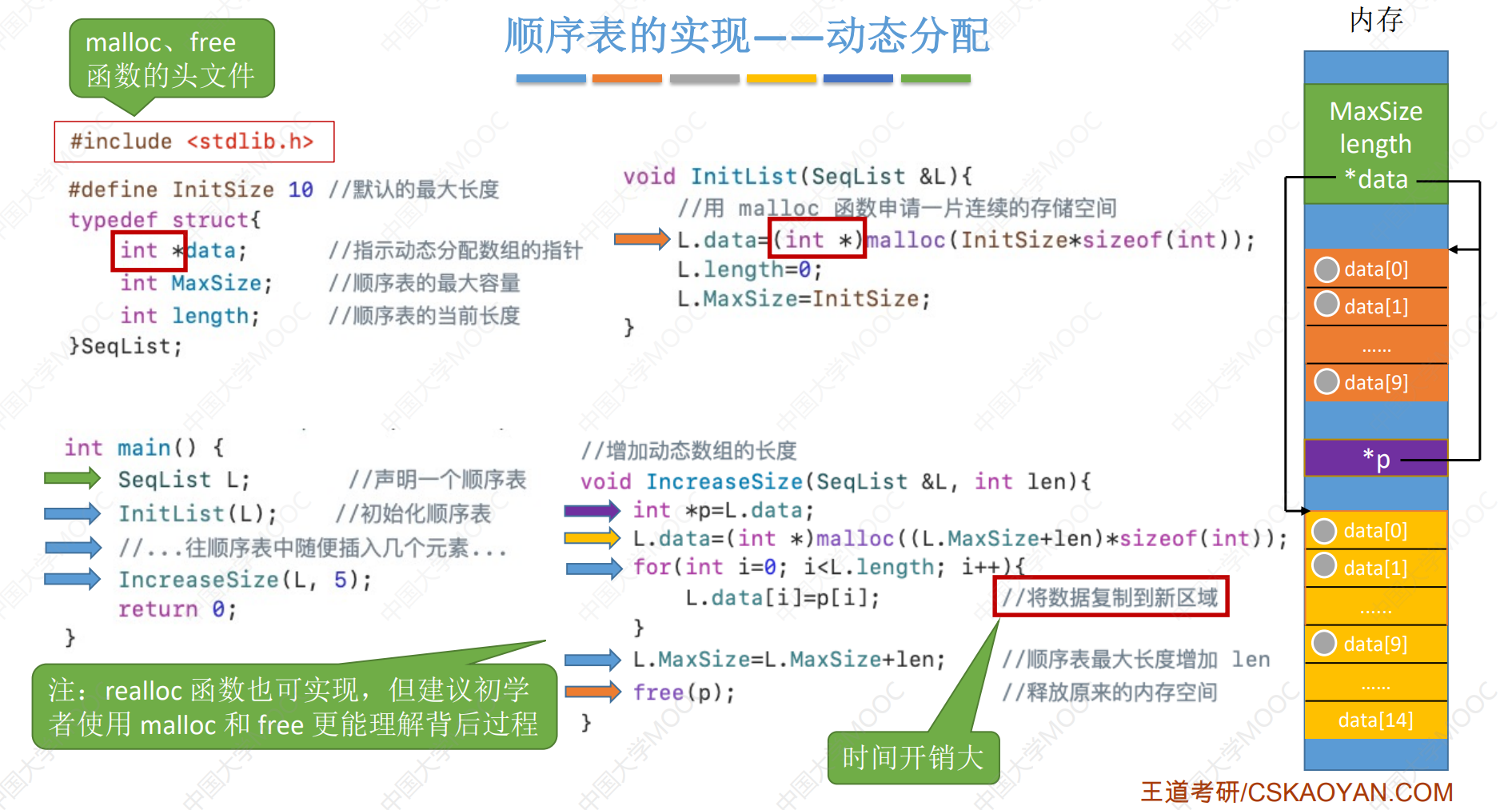
使用动态分配长度的方式定义线性表

typedef struct SeqList {
    int *data;
    int SizeMax;  // 顺序表的最大容量;
    int length;  // 顺序表当前最大长度;
} SeqL, *P;

/// 使用动态分配内存的方式进行分配;
/// \param P
void InitListChange(P P) {
    P->data = (int *) malloc(P->SizeMax * sizeof(int));
    P->length = 0;
    P->SizeMax = MaxSize;
}

void IncreaseSize(P P, int len) {
    int *p = P->data;  // 定义整形的指针, 并且将指针指向结构体中的指针
    // 将整形的内存长度加上指定的长度, 使用 malloc 函数申请内存, 并且转换成整形的指针;
    P->data = (int *) malloc((P->SizeMax + len) * sizeof(int));
    // 循环
    for (int i = 0; i < P->length; i++) {
        P->data[i] = p[i];  // 数据复制到新的区域;
    }
    P->SizeMax = P->SizeMax + len;  // 长度增加到 len;
    free(p);  // 释放申请的内存空间;
}

image-20240814220305732

2. 线性表的基本操作

InitList(&L)：初始化表。构造一个空的线性表L，分配内存空间。

DestroyList(&L)：销毁操作。销毁线性表，并释放线性表L所占用的内存空间。

以上两种主要是，从无到有，从有到无的操作；

ListInsert(&L,i,e)：插入操作。在表L中的第i个位置上插入指定元素e。

ListDelete(&L,i,&e)：删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值。

LocateElem(L,e)：按值查找操作。在表L中查找具有给定关键字值的元素。

GetElem(L,i)：按位查找操作。获取表L中第i个位置的元素的值。

其他常用操作：

  • Length(L)：求表长。返回线性表L的长度，即L中数据元素的个数。
  • PrintList(L)：输出操作。按前后顺序输出线性表L的所有元素值。
  • Empty(L)：判空操作。若L为空表，则返回true，否则返回false。

技巧：

  • 对数据的操作（记忆思路） —— 创销、增删改查

  • C语言函数的定义 —— <返回值类型> 函数名 (<参数1类型> 参数1，<参数2类型> 参数2，……）

  • 实际开发中，可根据实际需求定义其他的基本操作

  • 函数名和参数的形式、命名都可改变（Reference：严蔚敏版《数据结构》）

  • 什么时候要传入引用“&” —— 对参数的修改结果需要带回来。

2.1 顺序表的插入

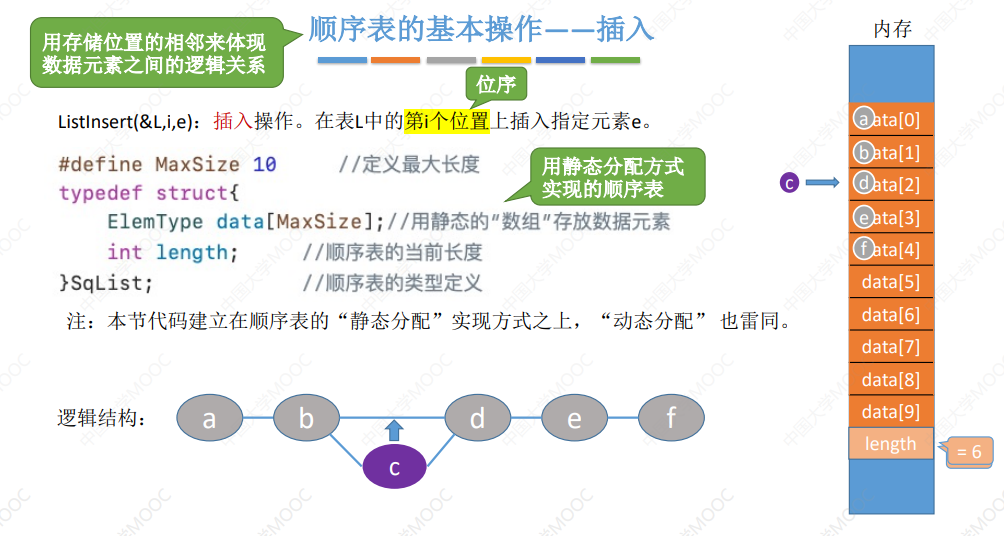
image-20240814221652086

#define MaxSize 10  // define 后面不需要加分号;

typedef struct SqList {
    int data[MaxSize];  // 使用静态数组存放数据元素;
    int length;  // 顺序表的当前长度
} SqList, *L;  // 顺序表类型的定义

/// 初始化线性表;
/// \param L 线性表结构体指针;
void InitList(L L) {
    for (int i = 0; i < MaxSize; i++) {
        L->data[i] = 0;
        L->length = i+1;
	}
}

/// 在顺序表的第 i 个位置插入指定元素 e;
/// \param L struct &SqList  顺序表的指针;
/// \param i int, 指定的位置;
/// \param e int, 需要插入的元素;
void ListInsert(L L, int i, int e){
    printf("start\n");
    printf("length: %d\n", L->length);
    for(int j=L->length;j<=i; j--){
        printf("now info %d\n", L->length);
        // 将插入元素的位置后的元素全部往后移动
        L->data[j]=L->data[j-1]; // 后移末尾元素;
    }
    printf("end for\n");
    // 赋值元素到指定的位置
    L->data[i-1]=e;  // 使用索引将元素进行赋值;
    L->length++; // 顺序表整体长度 +1
}


int main() {
    SqList linear_list;
    // 定义顺序表结构体的指针;
    L linear_list_point = &linear_list;
    // 初始化顺序表
    InitList(linear_list_point);
    // 在指定的位置进行插入;
    ListInsert(linear_list_point, 3, 6);


    // 打印数组的程序, 数组索引从 0 开始;
    for (int i = 0; i < 10; i++) {
        printf("index: %d, %d\n", i, linear_list_point->data[i]);
    }
    printf("This is linear list init success!");
    return 0;
}

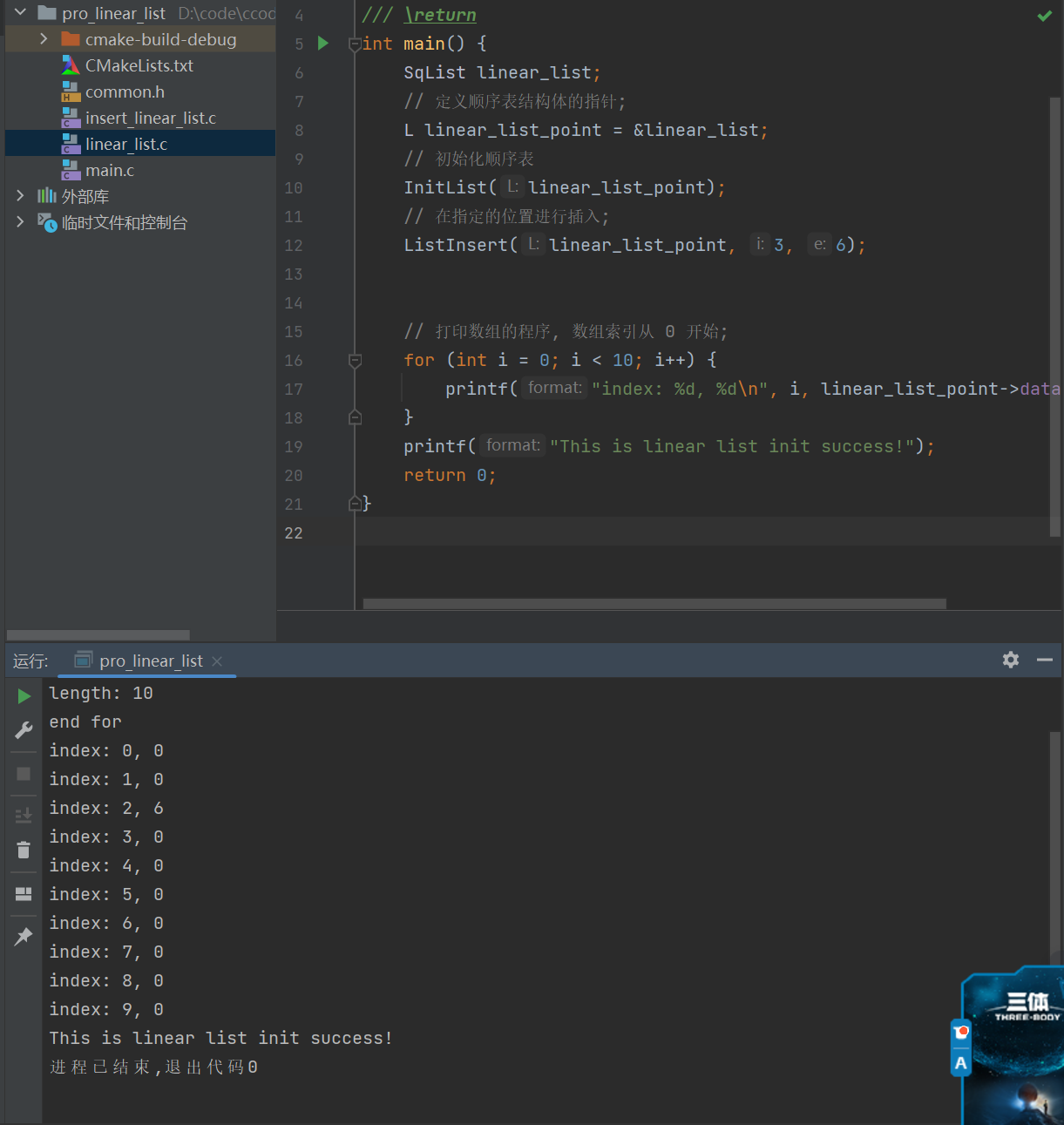
image-20240818185704370

当前的程序虽然能够完成元素的插入，但是程序的健壮性不够好，例如我们直接插入线性表最大值范围之外的数字就会保存，好的算法通常会具备处理异常的情况，虽然 C 语言没有提供相关的异常处理的语句，我们需要使用条件语句进行判断处理；

/// 在顺序表的第 i 个位置插入指定元素 e;
/// \param L struct &SqList  顺序表的指针;
/// \param i int, 指定的位置;
/// \param e int, 需要插入的元素;
void ListInsert(L L, int i, int e) {
    if (i < 1 || i > L->length + 1) {
        // return false;  c 语言中没有 bool 形的变量;
        printf("Error input param i\n");
        return;
    }
    if (i > MaxSize) {
        // 当前存贮空间已满, 不能进行插入;
        printf("Error input param i\n");
        return;
    }
    printf("start\n");
    printf("length: %d\n", L->length);
    for (int j = L->length; j <= i; j--) {
        printf("now info %d\n", L->length);
        // 将插入元素的位置后的元素全部往后移动
        L->data[j] = L->data[j - 1]; // 后移末尾元素;
    }
    printf("end for\n");
    // 赋值元素到指定的位置
    L->data[i - 1] = e;  // 使用索引将元素进行赋值;
    L->length++; // 顺序表整体长度 +1
}

加上条件判断直接规避错误参数的处理；

线性表插入元素的时间复杂度

  • 最好情况：新元素插入到表尾，不需要移动元素；i=n+1循环 0 次，最好时间复杂度：O(1)；

  • 最坏情况：新元素插入到表头，需要将原有的 n 个元素全部向后移动，i=1，循环 n 次，最坏时间复杂度：O(n)；

  • 平均复杂度：假设新元素插入到任何一个位置的概率相同，即i=1,2,3...，length + 1的概率相同都是1/n+1，平均时间复杂度：O(n)；

    image-20240818191920233

2.2 顺序表的删除

删除的操作是删除表中的第 i 个位置的元素，并用 e 返回删除元素的值，不在结尾的话需要将后续的位置进行前移；

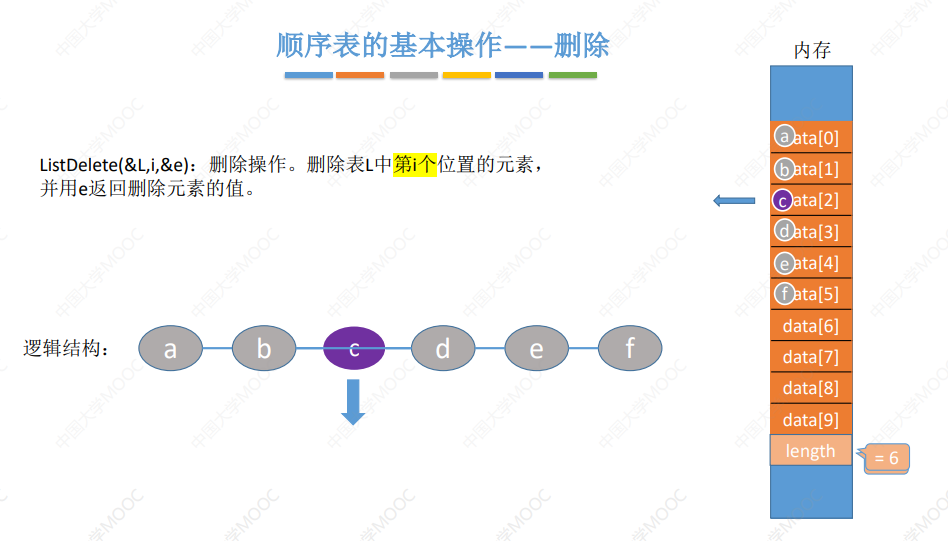
image-20240818192405247

void ListDelete(L L, int i, int *e) {
    if (i < 1 || i > L->length) {
        return;  // 判断 i 的范围是否有效;
    }
    *e = L->data[i - 1];  // 取出要删除的元素, 赋值给指针并传递给原来的参数;
    for (int j = i; j < L->length; j++) {
        // 将元素的位置进行向前的移动;
        L->data[j - 1] = L->data[i];
    }
    L->length--;  // 删除一个元素, 线性表的长度减一;
}


/// 主函数运行;
/// \return
int main() {
    SqList linear_list;
    // 定义顺序表结构体的指针;
    L linear_list_point = &linear_list;
    // 初始化顺序表
    InitList(linear_list_point);
    // 在指定的位置进行插入;
    ListInsert(linear_list_point, 1, 6);
    ListInsert(linear_list_point, 2, 6);
    ListInsert(linear_list_point, 3, 5);

    // 删除第三个元素;
    int e; // 定义一个元素用来接收被删除的元素;
    ListDelete(linear_list_point, 3, &e);

    printf("delete element is : %d\n", e);

    // 打印数组的程序, 数组索引从 0 开始;
    for (int i = 0; i < 10; i++) {
        printf("index: %d, %d\n", i, linear_list_point->data[i]);
    }
    printf("This is linear list init success!");
    return 0;
}

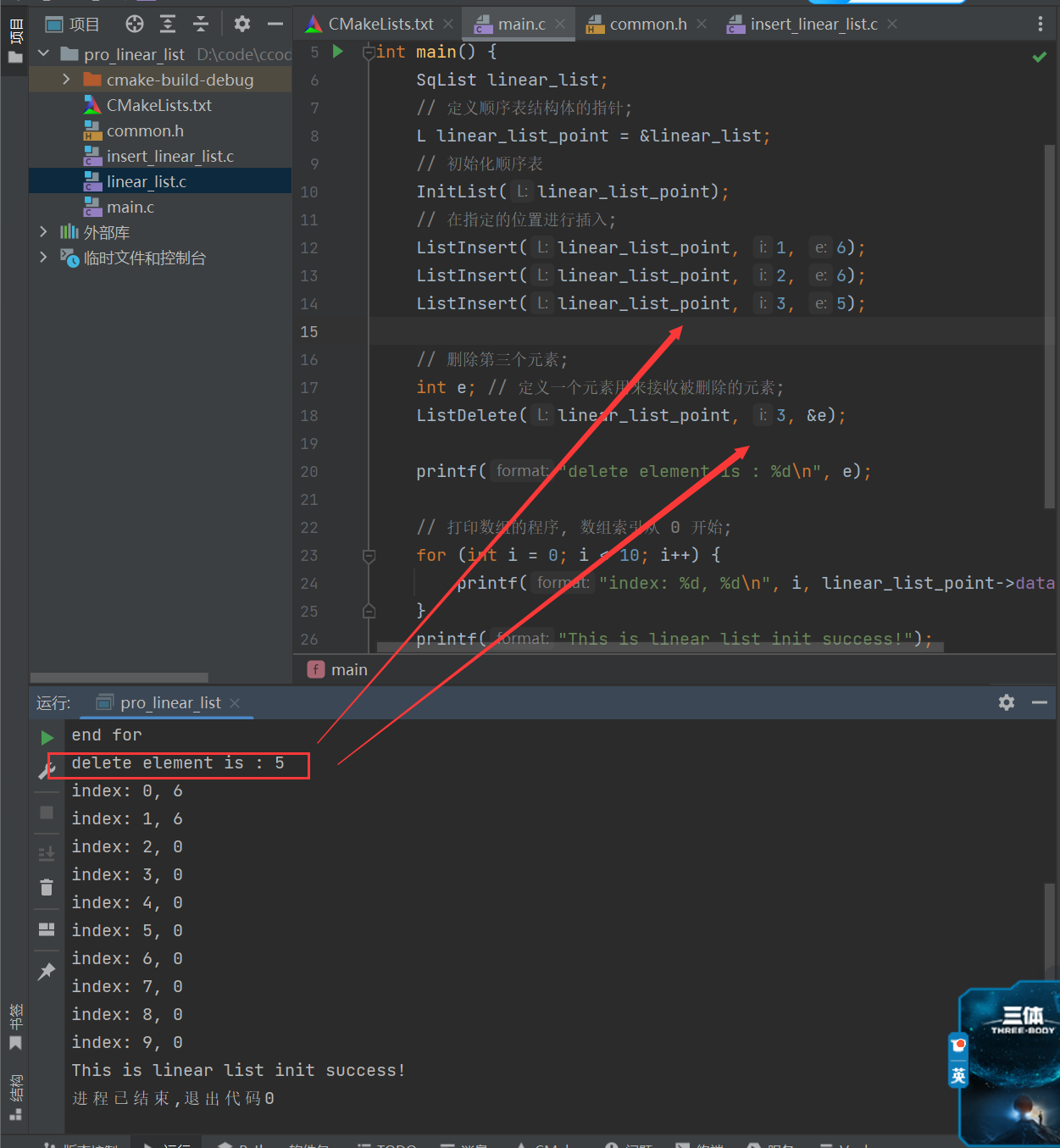
image-20240818224218641

  • 最好情况：删除表尾元素，不需要移动其他元素，i=n，循环 0 次；最好时间复杂度：O(1)；

  • 最坏情况：删除表头的元素，后面所有的元素都需要向前移动，i=1，循环 n-1次，最坏时间复杂度：O(n)；

  • 平均情况：假设删除任何一个元素的概率相同，即i=1,2,3...，length 的概率都是1/n；

    image-20240818224843060

2.3 顺序表的查找

顺序表的查找分为按位查找和按值查找两种方式；

  • 按位查找

    按位查找的操作，获取表 L 中第 i 个位置元素的值；

    typedef struct SqList {
    int data[MaxSize];  // 使用静态数组存放数据元素;
    int length;  // 顺序表的当前长度
} SqList, *L;  // 顺序表类型的定义


int IndexGetListItem(SqList List, int i) {
    // 获取线性表的指定位置的元素;
    // 位置-1 获取到数组的下标索引;
    return List.data[i - 1];
}


/// 主函数运行;
/// \return
int main() {
    SqList linear_list;
    // 定义顺序表结构体的指针;
    L linear_list_point = &linear_list;
    // 初始化顺序表
    InitList(linear_list_point);
    // 在指定的位置进行插入;
    ListInsert(linear_list_point, 1, 6);
    ListInsert(linear_list_point, 2, 6);
    ListInsert(linear_list_point, 3, 5);

    // 删除第三个元素;
    int e; // 定义一个元素用来接收被删除的元素;
    ListDelete(linear_list_point, 3, &e);
    // 获取位置 2 的元素;
    int res = IndexGetListItem(linear_list, 2);
    // 打印获取到的元素;
    printf("get element item is value : %d\n", res);

    printf("delete element is : %d\n", e);

    // 打印数组的程序, 数组索引从 0 开始;
    for (int i = 0; i < 10; i++) {
        printf("index: %d, %d\n", i, linear_list_point->data[i]);
    }
    printf("This is linear list init success!");
    return 0;
}

    image-20240819000709338

    按位查找的时候，都需要找到第一个元素从头开始查找，因此时间复杂度是O(1)；

  • 按值查找

    按值查找操作，在表 L 中查找具有给定关键字的元素值；

    int ElemGetList(SqList L, int e) {
    for (int i = 0; i < L.length; i++) {
        if (L.data[i] == e) {
            // 返回元素中的位序;
            return i + 1;
        }
    }
    // 未查找到;
    return 0;
}


int main() {
    SqList linear_list;
    // 定义顺序表结构体的指针;
    L linear_list_point = &linear_list;
    // 初始化顺序表
    InitList(linear_list_point);
    // 在指定的位置进行插入;

    for (int i = 0; i < MaxSize; i++) {
        ListInsert(linear_list_point, i, i * 10);
    }

    // 获取指定元素的位次;
    int response = ElemGetList(linear_list, 20);
    printf("response=%d\n", response);

    // 打印数组的程序, 数组索引从 0 开始;
    for (int i = 0; i < 10; i++) {
        printf("index: %d, %d\n", i, linear_list_point->data[i]);
    }
    printf("This is linear list init success!");
    return 0;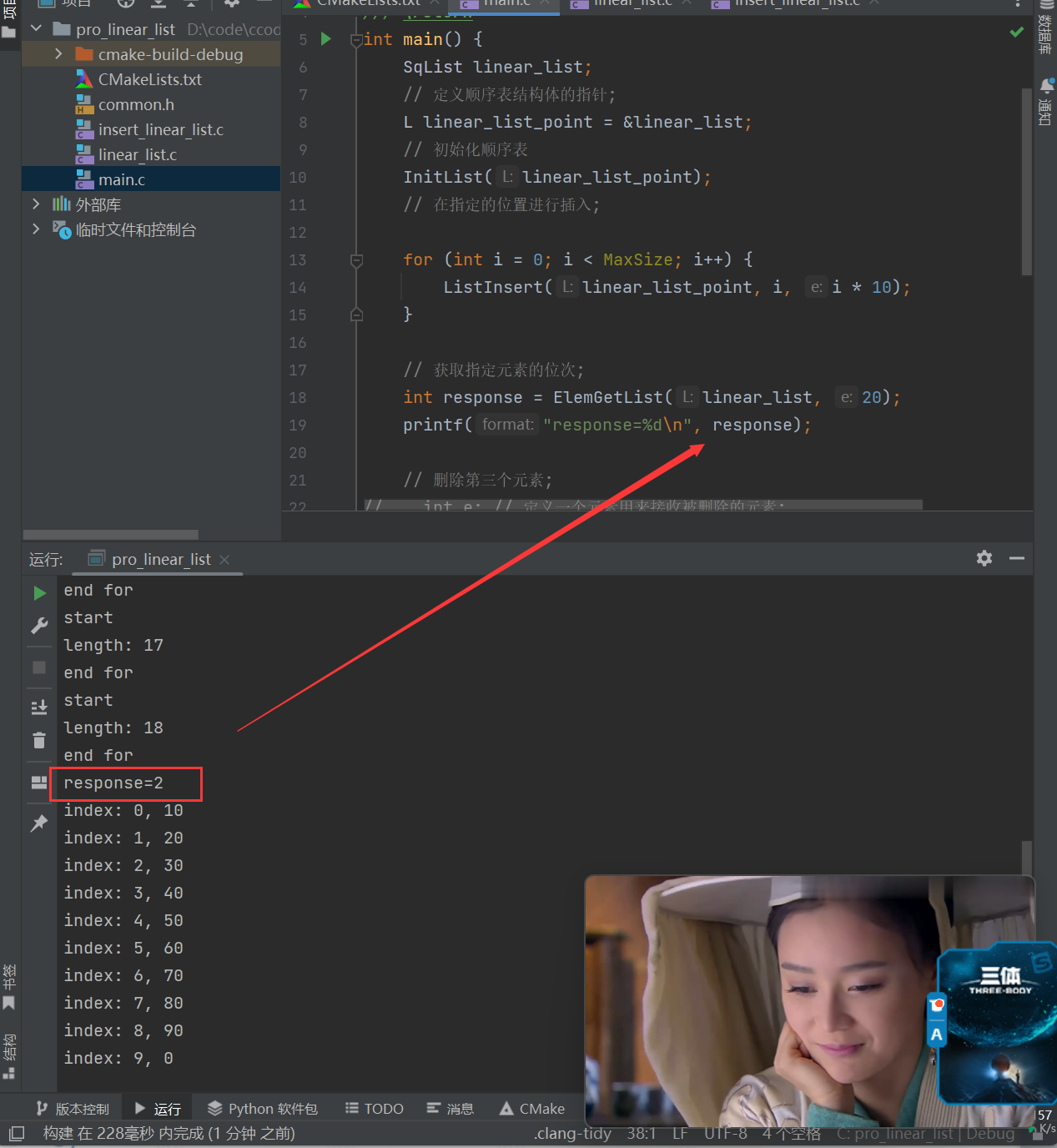
}

    image-20240819115028291

    值查找的时间复杂度：

    • 最好情况，目标元素在表头，循环 1 次， 最好时间复杂度=O(1)；

    • 最坏情况，目标元素在表尾，循环 n 次， 最坏时间复杂度=O(n)；

    • 平均情况，假设目标元素出现在任何一个位置的概率相同，都是1/n，平均时间复杂度=O(n)；

      image-20240819145632327

    补充：

    上述元素进行比较的时候使用的是==，基本数据类型 int、char、double、float 等可以直接运用运算符==比较；但是结构体不能够直接进行比较；

    typedef struct {
	int num;
	int people;
}Customer;

void test_struct() {
	Customer a;
	a.num = 1;
	a.people = 10;
	Customer b;
	b.num = 1;
	b.people = 1;
	// 不能使用 a==b 对结构体进行比较;
	// 结构体需要依次判断结构体的每一项进行比较
	if (a.num == b.num && a.people == b.people) {
		printf("相等\n");
	}
	else {
		printf("不相等\n");
	}
}


int main() {
    test_struct();
    return 0;
}

    image-20240819144837744

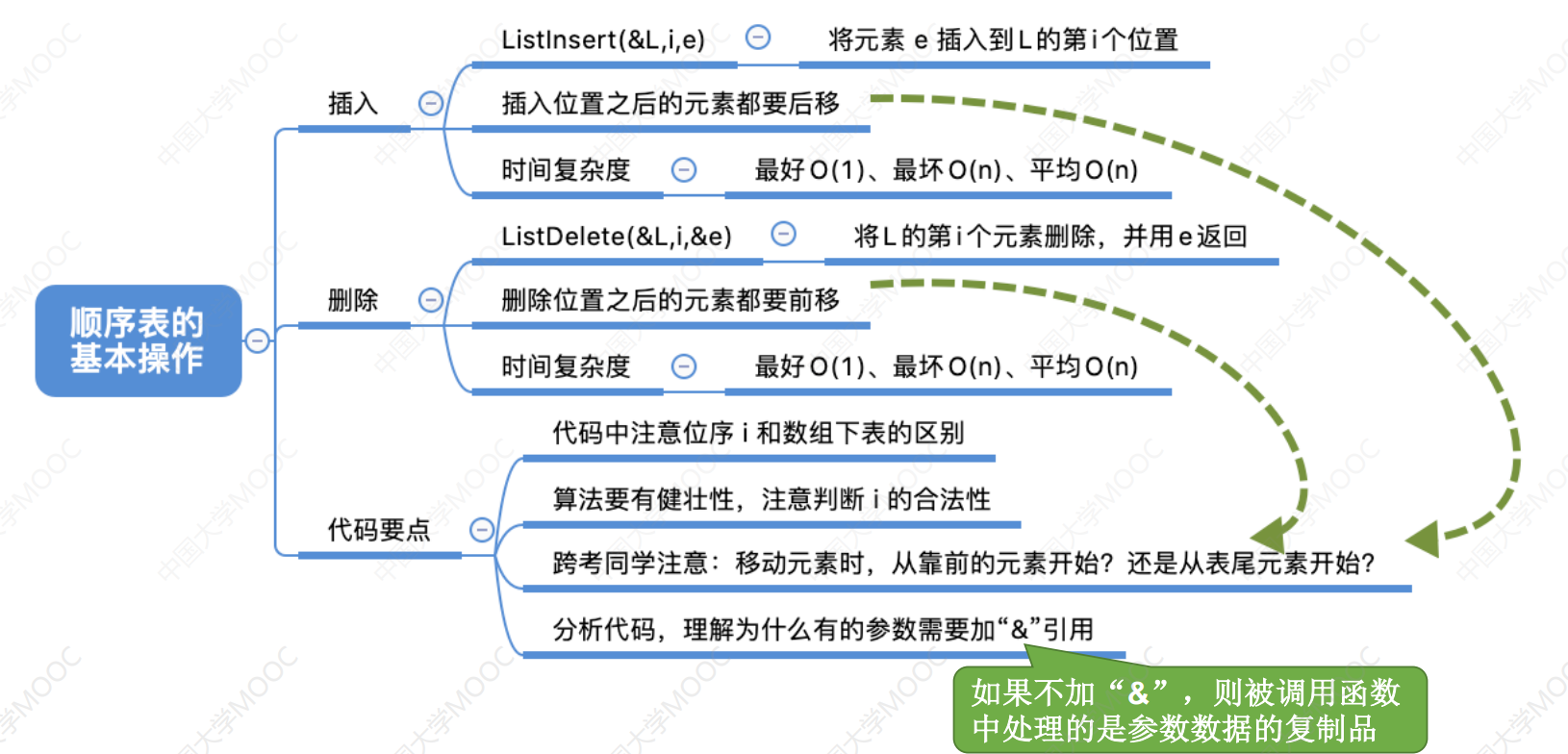
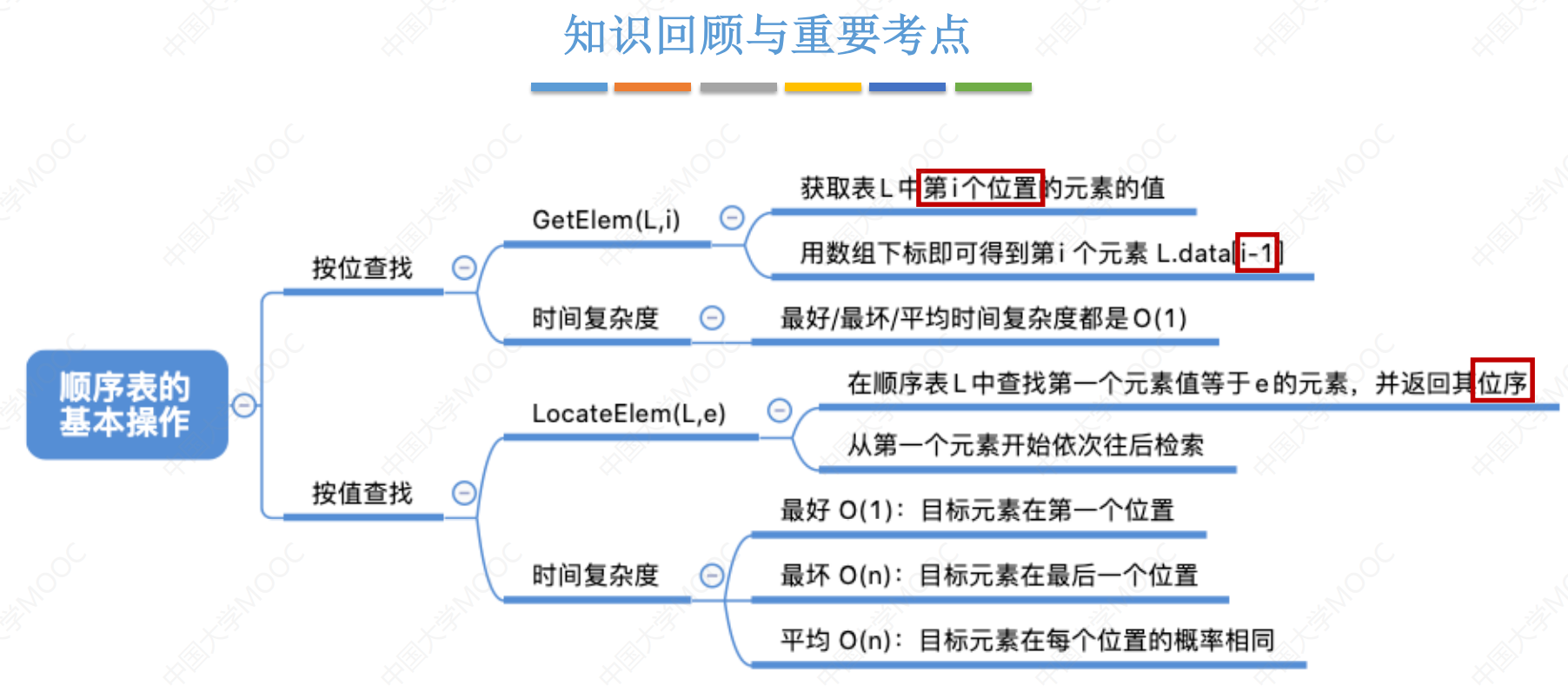
3. 顺序表的特点

  • 随机访问：即可以再O(1)时间内找到第 i 个元素；
  • 存储密度高，每个节点只存储数据元素；
  • 拓展不方便，即便采用动态分配的方式实现，拓展的时间复杂度也比较高；
  • 插入、删除，操作不方便，需要移动大量元素；

image-20240814220746107

image-20240818224943742

image-20240819145709382

度过大难，终有大成。

继续努力，终成大器。

标签：线性表,int,元素,list,指针,printf,数据结构,linear
From： https://www.cnblogs.com/Blogwj123/p/18367320

相关文章

  • 基础数据结构回顾记录
    数组初始化两种方式声明和初始化数组——使用new关键字和使用大括号。refer:https://www.freecodecamp.org/chinese/news/java-array-declaration-how-to-initialize-an-array-in-java-with-example-code/先声明，后赋值//数组声明dateType[]nameOfArray=newdataType......
  • 【数据结构与算法】如何构建最小堆
    最小堆的定义最小堆，作为一种独特且重要的数据结构，它是一种特殊的二叉树。在这种二叉树中，有一个关键的规则：每一个父节点所存储的值，都必然小于或者等于其对应的子节点的值。这一规则确保了根节点总是承载着整个堆中的最小数值。例如，下面这样一个简单的结构就是最小堆：1......
  • 【数据结构】详细剖析链表，带你实现单链表，双向链表，附链表编程练习题
    目录一.链表1.链表的概念及结构2.单链表的实现2.1单链表节点结构2.2动态申请一个节点2.3单链表打印2.4单链表尾插2.5单链表头插2.6单链表尾删2.7单链表头删2.8单链表查找 2.9单链表在pos后一位插入x2.10单链表删除pos后一位的值2.11单链表销毁 ......
  • 知识改变命运 数据结构【链表面试题】
    1.删除链表中等于给定值val的所有节点。OJ链接publicListNoderemoveElements(ListNodehead,intval){if(head==null){returnnull;}ListNodecur=head.next;ListNodepre=head;while(cur!=null){......
  • 数据结构--顺序表
    目录一、引言二、顺序表的基本概念与结构1.概念2.基本结构三、顺序表的分类四、动态顺序表的实现 1.结构定义2.相关功能实现1.初始化2.销毁3.扩容4.打印 5.头插6.尾插 7.头删 8.尾删 9.指定插入 10.指定删除 11.查找  五、完整代码1.SeqList.h2......
  • 【模板】数据结构
    数据结构权值BIT上二分struct{intn,t[N]; intkth(intk){ intp=0;rFor(i,__lg(n),0)if(p+(1<<i)<n&&k>t[p+(1<<i)])p+=1<<i,k-=t[p]; returnp+1; }};zkw线段树李超线段树线段树合并，分裂可持久化\(01......
  • 数据结构----链表
    一丶概念     链表又称单链表、链式存储结构，用于存储逻辑关系为“一对一”的数据。      和顺序表不同同，使用链表存储数据，不强制要求数据在内存中集中存储，各个元素可以分散存储在内存中。二丶特点     特点：内存不连续，通过指针进行连接 ......
  • 数据结构与算法——BFS(广度优先搜索)
    算法介绍：广度优先搜索（Breadth-FirstSearch，简称BFS）是一种遍历或搜索树和图的算法，也称为宽度优先搜索，BFS算法从图的某个节点开始，依次对其所有相邻节点进行探索和遍历，然后再对这些相邻节点的相邻节点进行探索，直到遍历完所有的节点。BFS算法使用队列来辅助实现，将起始节点放入队列......
  • 数据结构中的双向链表
    1.链表的分类链表的结构非常多样，以下情况组合起来就是8种（2x2x2）链表结构：  在带头链表中，除了头结点，其他结点均存储有效的数据。头结点是占位子的，也叫做“哨兵位”。head结点就是头结点。 循环的链表尾结点不为NULL，不循环的链表尾结点为NULL单链表：不带头单向不循环链......
  • 数据结构与算法（五）栈
    一.定义：栈是限定仅在表尾进行插入或删除操作的线性表，因此，对栈来说，表尾端具有其特殊含义，称为栈顶（top），表头端称为栈底（bottom）。不含元素的空表称为空栈。栈是重要的线性结构之一，从数据结构的角度来说，栈也是线性表在理解栈的含义要注意：首先，它是一个线性表，也就是说栈元素具有线性......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99