AC 自动机

前言

我觉得AC自动机这种东西非常抽象，有必要写一篇博客来整理一下，以加深理解。

概况

AC自动机是以 Trie 树的结构为基础，结合 KMP 思想建立的自动机，用于解决多模式串匹配等任务。

一般来说，建立一个AC自动机有两个步骤：

1. 把所有的模式串建成一颗 Trie 树。
2. 用 KMP 的思想对 Trie 树上所有的节点构建失配指针。

字典树构建

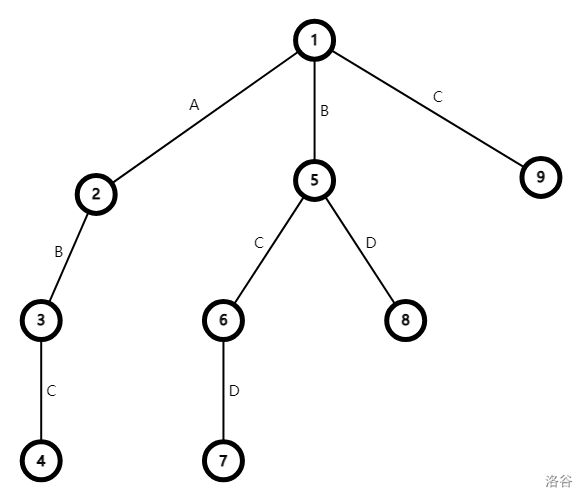
字典树即 Trie 树，它的构建不必多说。拿 ABC、BCD、BD、C 这四个字符串举个例子，构建出来的 Trie 树就是这个样子（如图1），为了方便，我们把每个节点所代表的字符作为它的入度的边的边权。

void insert(char s[]) {
	int u = 1, len = strlen(s);
	for (int i = 0; i < len; i++) {
		int v = s[i] - 'a';
		if (!trie[u][v]) trie[u][v] = ++tot;
		u = trie[u][v];
	}
	cnt[u]++; // 具体看情况
}

失配指针

含义

失配指针即 fail 指针，我们记 $u$ 的 fail 指针为 $fail[u]$。对于 $u$ 节点所对应的字符串而言，AC 自动机上的所有字符串当中，$fail[u]$ 为该字符串的最长后缀。举个例子，图1中，节点 4 对应的字符串为 ABC，它在 AC 自动机上能找到的最长后缀是 BC，所以节点 4 的 fail 指针指向 6。

构建

首先我们显然可以知道，一个节点的 fail 指针指向的点的深度一定是比该点要小的。所以 $fail[1]$ 就是 $root$（也就是 $0$）。

设点 $u$ 下的字符 $i$ 所对应的节点为 $trie[u][i]$。

1. 若存在节点 $trie[u][i]$，则 $fail[trie[u][i]]=trie[fail[u]][i]$。还是拿图1举例子，现在以求出 $fail[3]=5$，那么 $fail[trie[3][C]]=trie[fail[3]][C]$ 即 $fail[4]=6$。
2. 若不存在节点 $trie[u][i]$（即 $trie[u][i]=0$），则 $trie[u][i]=trie[fail[u]][i]$ 。依旧是拿图1举例子，显然节点 $trie[3][D]$ 不存在，而 $fail[3]$ 和 $3$ 所代表的字符串（后缀）是相同的，所以我们从 $3$ 向 $trie[fail[3]][D]$ 连一条边，即从 $3$ 向 $7$ 连一条边，这样节点 $trie[3][D]$ 就存在了。
3. 因为要求出父亲节点的 fail 再求儿子的 fail，所以我们用广搜来实现。

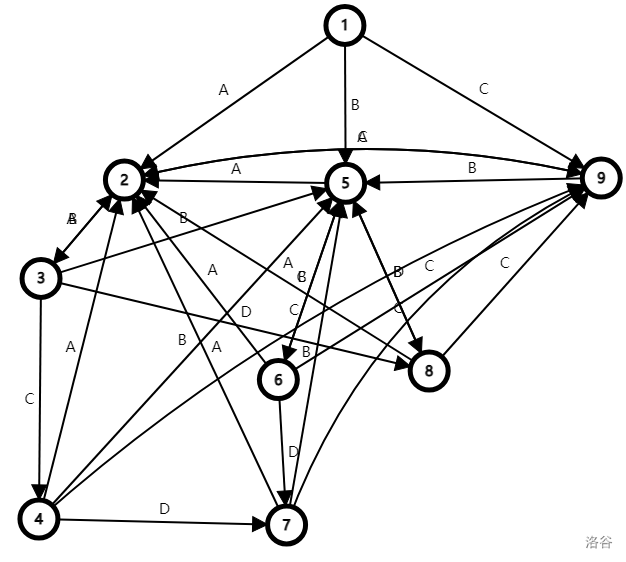
然后我们的 trie 树（图）就会变成这个样子，如图2。虽然很抽象，但凑合着还能看。

void getfail() {
	for (int i = 0; i < 26; i++) trie[0][i] = 1;	// 初始化0的所有儿子都是1
	q.push(1);										// 将根压入队列
	fail[1] = 0;
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; i++) {				// 遍历所有儿子
			if (!trie[u][i]) {						// 如果不存在该节点，对应 2
				trie[u][i] = trie[fail[u]][i];		// 从u向trie[fail[u]][i]连一条边
				continue;
			}
			fail[trie[u][i]] = trie[fail[u]][i];	// 求fail，对应 1
			q.push(trie[u][i]);						// 将实点压入队列
		}
	}
}

怎么用

这还用说吗？看着用呗。

代码

拿例题来说事儿吧。[HDU 2222]Keywords Search

#include <bits/stdc++.h>

using namespace std;

const int N = 1e4 + 10, M = 1e6 + 10;
int n, t;
char s[M];
int trie[M][26], cnt[M], flag[M], fail[M];
int tot;
queue<int> q;
void insert(char s[]) { // 构建trie树
	int u = 1, len = strlen(s);
	for (int i = 0; i < len; i++) {
		int v = s[i] - 'a';
		if (!trie[u][v]) trie[u][v] = ++tot;
		u = trie[u][v];
	}
	cnt[u]++;
}
void getfail() {
	for (int i = 0; i < 26; i++) trie[0][i] = 1;	// 初始化0的所有儿子都是1
	q.push(1);										// 将根压入队列
	fail[1] = 0;
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; i++) {				// 遍历所有儿子
			if (!trie[u][i]) {						// 如果不存在该节点，对应 2
				trie[u][i] = trie[fail[u]][i];		// 从u向trie[fail[u]][i]连一条边
				continue;
			}
			fail[trie[u][i]] = trie[fail[u]][i];	// 求fail，对应 1
			q.push(trie[u][i]);						// 将实点压入队列
		}
	}
}
int query(char s[]) {
	int u = 1, len = strlen(s), ans = 0;
	for (int i = 0; i < len; i++) {
		int v = s[i] - 'a';
		int k = trie[u][v];
		while (k > 1 && flag[k] != -1) {
			ans = ans + cnt[k];
			flag[k] = -1;
			k = fail[k]; // 如果当前节点可以匹配成功的话，那么它的fail一定也可以
		}
		u = trie[u][v];
	}
	return ans;
}
void solve() {
	memset(trie, 0, sizeof(trie));
	memset(flag, 0, sizeof(flag));
	memset(fail, 0, sizeof(fail));
	memset(cnt, 0, sizeof(cnt));
	tot = 1; 			// 这十分重要
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%s", s); // 读入模式串
		insert(s); 		// 把模式串扔到trie树里
	}
	getfail();
	scanf("%s", s);		// 读入文本串
	printf("%d\n", query(s)); // 拿文本串查询
}
int main() {
	scanf("%d", &t);
	while (t--) {
		solve();
	}
	return 0;
}

AC 自动机上 DP

懵了吧？因为 AC 自动机本质上是 trie 树，是一棵树，所以他自然是可以 dp 的。既然它是一棵树，那就可以进行更多的树上操作，比如树剖。

AC 自动机上 dp 一般比较套路。$dp_{i,j}$ 表示当前在 $i$ 节点，且串长为 $j$ 的情况。有时候再加一维表示选了些什么（状压）。

然后就没了。