KMP(Knuth-Morris-Pratt)
用途:
用于一个文本串S内查找一个模式串P 的出现位置,以及求一个字符串的最小循环元长度和最大循环次数。
思路:
\(kmp\)是对原始的在文本串S内查找一个模式串P的出现位置的一种优化。
原始做法
将\(s\)的每一位都与\(p\)的第一位开始匹配。
(匹配到\(s\)的第\(i\)位和\(p\)的第\(j\)位。\(i\),\(j\)从0开始)
if(s[i]==p[j])i++,j++;//匹配成功,同时加1
else i=i-j+1,j=0;//j变成0,匹配的起始点向右移一位
\(kmp\)做法
匹配不成功,\(i\)不变,\(j=nxt[j]\)
\(nxt[j]\)表示\(j\)的最长前后缀,eg. \(abacaba\)中\(aba\)是最长前后缀,\(a\)也是它的前后缀但不是最长的;
这样匹配,合理的运用了前面匹配的信息,只有前后缀才有可能成为答案,理由很显然,这样可以避免一些无用的枚举。
直接求\(nxt\)t的复杂度是\(n^2\),所以考虑优化。
i的前后缀一定是\(i-1\)的前后缀\(+1\),因为将\(i\)掉,剩下的一定满足前后缀。
所以只要不停跳\(i-1\)的前后缀,可以快速求\(nxt\).
void gnxt()
{
int j=0;
int len=strlen(p+1);
for(int i=2;i<=len;i++)
while(j&&p[i]!=p[j+1]) j=nxt[j];//找一个前后缀满足下一位相同
if(p[i]==p[j+1])j++;//符合条件j匹配下一位
nxt[i]=j;//记录
}
return ;
}
模式串与文本串匹配与求\(nxt\) 的过程相似,
int s1=strlen(s+1);
int s2=strlen(p+1);
int i=0,j=0;
for(int i=1;i<=s1;i++)
{
while(j&&s[i]!=p[j+1]) j=nxt[j];
if(s[i]==p[j+1])j++;
if(j==s2)printf("%d\n",i-j+1),j=nxt[j];
}
return ;
EXKMP
用途:
能在 \(O(|a|+|b|)\) 的时间内处理出文本串 \(a\)的所有后缀和模式串 \(b\) 的最长公共前缀。
流程(图片来自洛谷):
求\(nxt[i]\)(\(nxt[i]\)表示模式串\(b\)与模式串\(b\)以\(b[i]\) 开头的后缀的最长公共前缀的长度)如下图
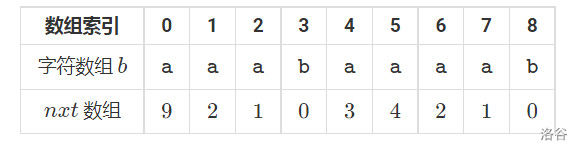
假设求\(nxt[x]\)时所有\(nxt[j](0\le j<x)\) 都已经求出来了。
定义\(p\) 是\(max(i+nxt[i]-1)\),\(k\)是这个最大的\(i\).可知蓝色段相同
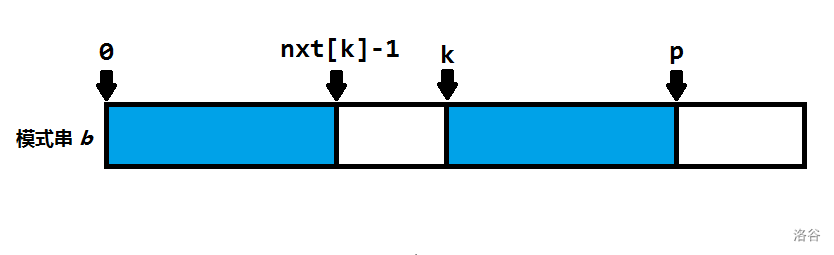
加上当前点\(x\) ,可知绿色段相同
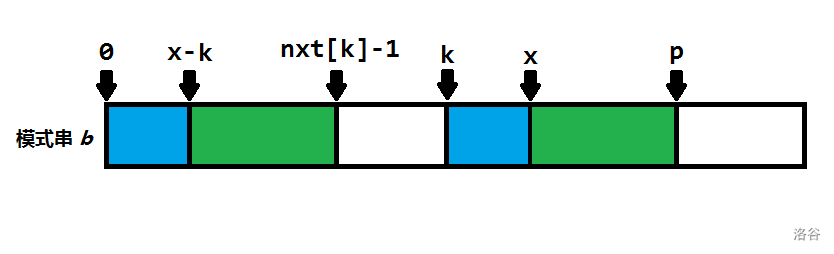
因为绿色段相同,\(nxt[x-k]\) 对计算 \(nxt[x]\) 有帮助。
如果\(x-k+nxt[x-k]-1<nxt[k]-1\) 那么 \(nxt[x]=nxt[x-k]\) (显然灰色部分相同且\(l-1\)到 \(x-k\)的蓝色部分与剩下的绿色不同,不然\(nxt[x-k]\) 应该包括它们)
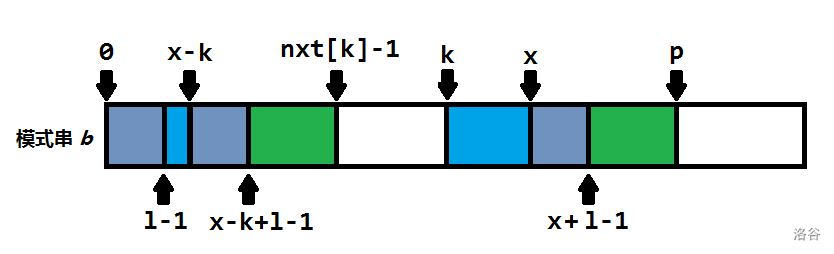
如果比它大,显然 \(nxt[x]>=(nxt[k]-1-(x-k))\) 整个绿色都是公共前缀,\(p\) 的后面不一定相同所以,\(p\) 和\(l-1\)一个一个暴力比较计算\(nxt[x]\) 。
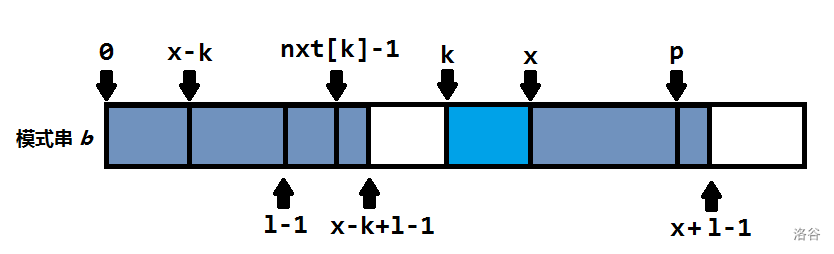
正确性显然,时间复杂度参考\(manacher\) 算法。
void qnxt(char *c)
{
int len = strlen(c);
int p = 0, k = 1, l; //我们会在后面先逐位比较出 nxt[1] 的值,这里先设 k 为 1
//如果 k = 0,p 就会锁定在 |c| 不会被更改,无法达成算法优化的效果啦
nxt[0] = len; //以 c[0] 开始的后缀就是 c 本身,最长公共前缀自然为 |c|
while(p + 1 < len && c[p] == c[p + 1]) p++;
nxt[1] = p; //先逐位比较出 nxt[1] 的值
for(int i = 2; i < len; i++)
{
p = k + nxt[k] - 1; //定义
l = nxt[i - k]; //定义
if(i + l <= p) nxt[i] = l; //如果灰方框小于初始的绿方框,直接确定 nxt[i] 的值
else
{
int j = max(0, p - i + 1);
while(i + j < len && c[i + j] == c[j]) j++; //否则进行逐位比较
nxt[i] = j;
k = i; //此时的 x + nxt[x] - 1 一定刷新了最大值,于是我们要重新赋值 k
}
}
}
- 求\(ext[i]\)
我们用 \(ext[i]\) 表示“模式串 \(b\)” 与 “文本串 \(a\) 以 \(a[i]\) 开头的后缀” 的 “最长公共前缀” 的长度。
与求\(nxt[i]\) 的方法相同,\(nxt[i]\)是自己与自己匹配而已
void exkmp(char *a, char *b)
{
int la = strlen(a), lb = strlen(b);
int p = 0, k = 0, l;//ext[0]!=|c|,所以预处理0,从一开始递推
while(p < la && p < lb && a[p] == b[p]) p++; //先算出初值用于递推
ext[0] = p;
for(int i = 1; i < la; i++) //下面都是一样的逻辑啦
{
p = k + ext[k] - 1;
l = nxt[i - k];
if(i + l <= p) ext[i] = l;
else
{
int j = max(0, p - i + 1);
while(i + j < la && j < lb && a[i + j] == b[j]) j++;
ext[i] = j;
k = i;
}
}
}