国令783号《公平竞争审查条例》已于今年8月1日震撼登场,这一国家级法规的出台,对产业园区这一经济发展的重要载体而言,无疑是一颗投入深水中的重磅炸弹,其引发的连锁反应将深远地重塑产业园区的运营生态,开启一个全新的竞争时代!
条例解析,对产业园区运营的影响
重塑规则,挑战与机遇并存

税收优惠与奖补模式的终结:
国令783号第十条明确规定,政策措施不得含有影响生产经营成本的内容,如给予特定经营者的税收优惠、财政奖励或补贴等。这一条款如同一道紧箍咒,让以往产业园区通过“撒钱”吸引特定企业的老路彻底走到了尽头。产业园区必须摒弃过去依赖简单优惠政策的短视行为,转而注重提升园区的综合竞争力和服务水平,以软实力吸引企业入驻。

行政干预市场的终结:
条例第十一条更是对行政权力划定了明确的界限,禁止政策措施含有影响生产经营行为的内容,如强制或变相强制企业实施垄断行为、超越法定权限制定价格等。这要求产业园区在租赁运营中必须遵循市场规则,尊重企业的自主经营权,通过公平透明的市场环境赢得企业的信任。
公平竞争,市场环境的净化

然而,条例并非一刀切地禁止所有特殊政策。第十二条为产业园区在特定情况下制定和实施特殊政策提供了一定的灵活空间,但前提是必须符合法定条件,且对公平竞争的影响最小。这一条款鼓励产业园区在科技创新、环境保护等社会公共利益领域积极探索,但必须在公平竞争的框架内行事。
简单来说,国令783号《公平竞争审查条例》对产业园区运营影响主要体现在以下三个方面:
01 招商引资模式的转变
随着税收优惠和财政补贴等优惠措施的受限,产业园区需要转变传统的招商引资模式。未来,产业园区将更加注重提升园区的整体竞争力和服务水平,通过优化营商环境、完善基础设施、提供高效服务等方式吸引企业入驻。
02 市场竞争的规范化
条例的实施将促进市场竞争的规范化,防止产业园区通过行政手段干预市场竞争。这将有助于维护企业的自主经营权,促进市场资源的合理配置和高效利用。同时,也将推动产业园区内企业之间的公平竞争,激发市场活力。
03 园区运营的数字化转型
面对新的挑战和机遇,产业园区需要加快数字化转型的步伐。通过引入数字化平台和技术手段,提升园区运营效率和管理水平,实现精细化管理和智能化服务。这不仅有助于提升园区的整体竞争力,还能为园区内企业提供更加便捷、高效的服务。
璞华易商:助力产业园区破局前行
面对《公平竞争审查条例》带来的新挑战和机遇,璞华易商作为产业园区运营管理平台,凭借其强大的数字化能力和专业的服务能力,为产业园区提供了全方位的助力。
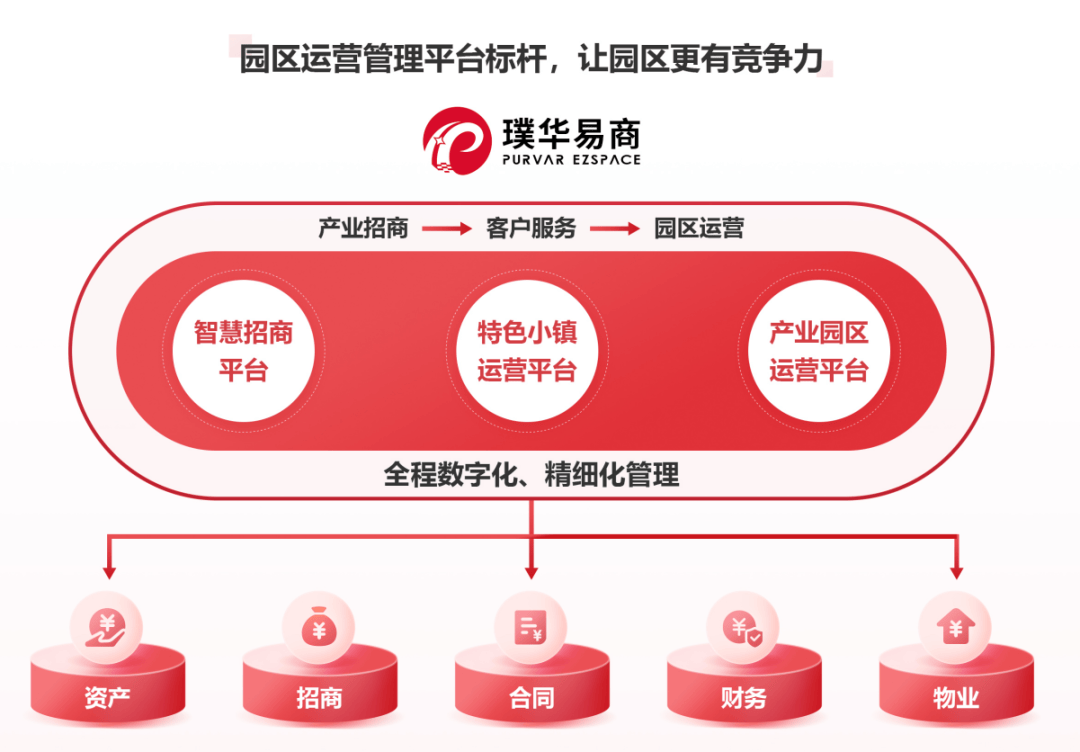
01 全流程数字化整合,提升运营效率
璞华易商通过集成客户管理、房源管理、租赁合同、财务应收、物业管理等功能于一体,实现了园区运营的全流程数字化整合。这不仅大幅提升了管理效率,还通过精细化管理全面提升了园区的经营效益。自动化与智能化服务更是让园区运营如虎添翼,减少了人工操作,提高了数据处理的准确性和效率。
02 促进公平竞争与合规经营
璞华易商平台协助园区管理者更好地理解和执行《公平竞争审查条例》等相关政策,确保园区的运营行为合规合法。透明化的租赁合同签订和租金确定过程减少了信息不对称和潜在的不公平竞争行为,维护了园区内企业的合法权益。
03 优化资源配置与提升竞争力
璞华易商通过精准的市场动态分析和资源配置建议,帮助园区管理者更好地把握市场机遇和租赁趋势。同时,平台提供的全方位服务如物业管理、财务咨询等也提升了园区的服务品质,增强了企业的满意度和忠诚度。
04 助力产业园区转型升级
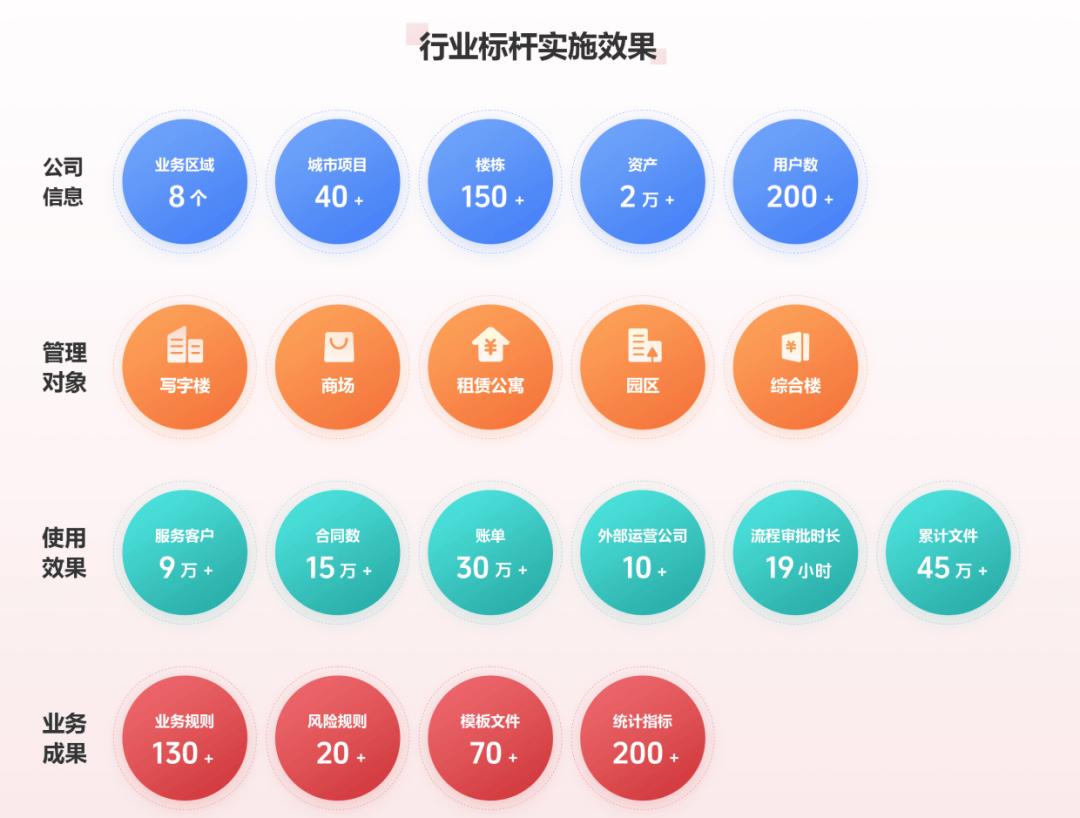
在数字化转型的大潮中,璞华易商为产业园区提供了强有力的支持。璞华易商提供第三数据源接入8+、文件内容自动采集、账单自动生成等服务,提供动态管理空间资源的在租、空置状态,提供动态租金定价策略10+、合同条款参数配置30+、自动生成账单模板10+、统计指标项100+,实现用户的数据录入、整理、分析工作效率提升,实现租赁运营工作协同、决策智能的能力提升。

通过数字化转型和创新服务模式的探索与实践,产业园区可以更加高效地管理运营、提升服务品质、降低运营成本,从而在激烈的市场竞争中脱颖而出。
国令783号《公平竞争审查条例》的出台标志着产业园区运营进入了一个全新的时代。面对新的挑战和机遇,产业园区需要与时俱进、勇于创新。而璞华易商作为产业园区租赁运营平台的佼佼者,将携手产业园区共同迎接这个新时代的挑战与机遇!
志合者,不以山海为远。数字化转型、智能化升级的道路上需要同路人,我们将与广大用户一路前行。如果您有什么需求或者疑问,请随时与我们联系。
标签:数字化,产业园,783,条例,国令,运营,公平竞争,园区 From: https://www.cnblogs.com/purvar/p/18350766