后缀数组(suffix array)是一个通过对字符串的所有后缀经过排序后得到的数组。后缀数组被 Manber 和 Myers 于1990年提出, 作为对后缀树的一种替代, 更简单以及节省空间。它们也被Gaston Gonnet 于1987年独立发现, 并命名为“PAT数组”。
后缀数组有很多奇妙的性质, 这些性质可以帮助解决很多字符串问题(然后出串串题虐死别人)。
板子题:
\(O(n \log^2 n)\) 做法
后缀 \(i\) 代指以第 \(i\) 个字符开头的后缀, 也称 \(suff(i)\), 本文规定字符串下标从 \(1\) 开始, 后文都将使用数组式下标。
首先朴素的想, 将 \(n\) 个后缀直接塞进 string 数组内大力 sort, 很不幸 STL 提供的 string 类型比较字典序的复杂度为 \(O(n)\), 我们只能得到 \(O(n^2 \log n)\) 的暴力。
回想一下我们比较字符串的字典序的过程:
1.从第一个字符开始比较。
2.如果当前字符不相等,就直接比较这两个字符,即可得出答案。
3.否则,继续比较下一个字符。
这个过程实际上就是在寻找两个字符串的最长公共前缀,而下一个字符就一定不相等。最长公共前缀是具有单调性的,哈希上二分一下就能 \(O(\log n)\) 比较字典序,这样我们的算法就优化到了 \(O(n \log^2 n)\)。这个复杂度已经可以通过洛谷的模板题了(代码)。
复杂度瓶颈在排序和求 \(LCP\), 不好优化, 考虑另一种 \(O(n \log^2 n)\) 的做法:
先按照每个后缀的第一个字符排序。对于每个字符,我们按照字典序给一个排名(当然可以并列), 这里称作关键字。
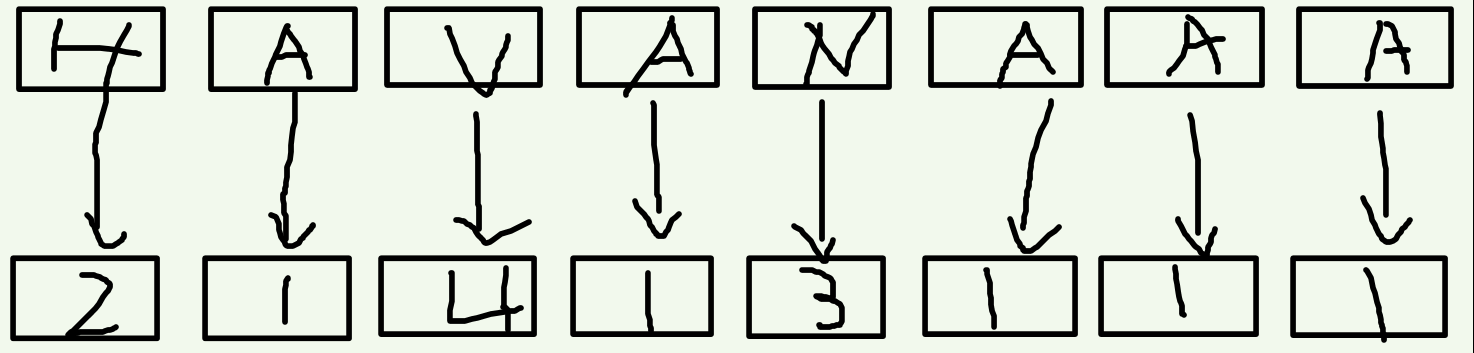
接下来我们再把相邻的两个关键字合并到一起,就相当于根据每一个后缀的前两个字符进行排序。想想看,这样就是以第一个字符(也就是自己本身)的排名为第一关键字,以第二个字符的排名为第二关键字,把组成的新数排完序之后再次标号。没有第二关键字的补零。
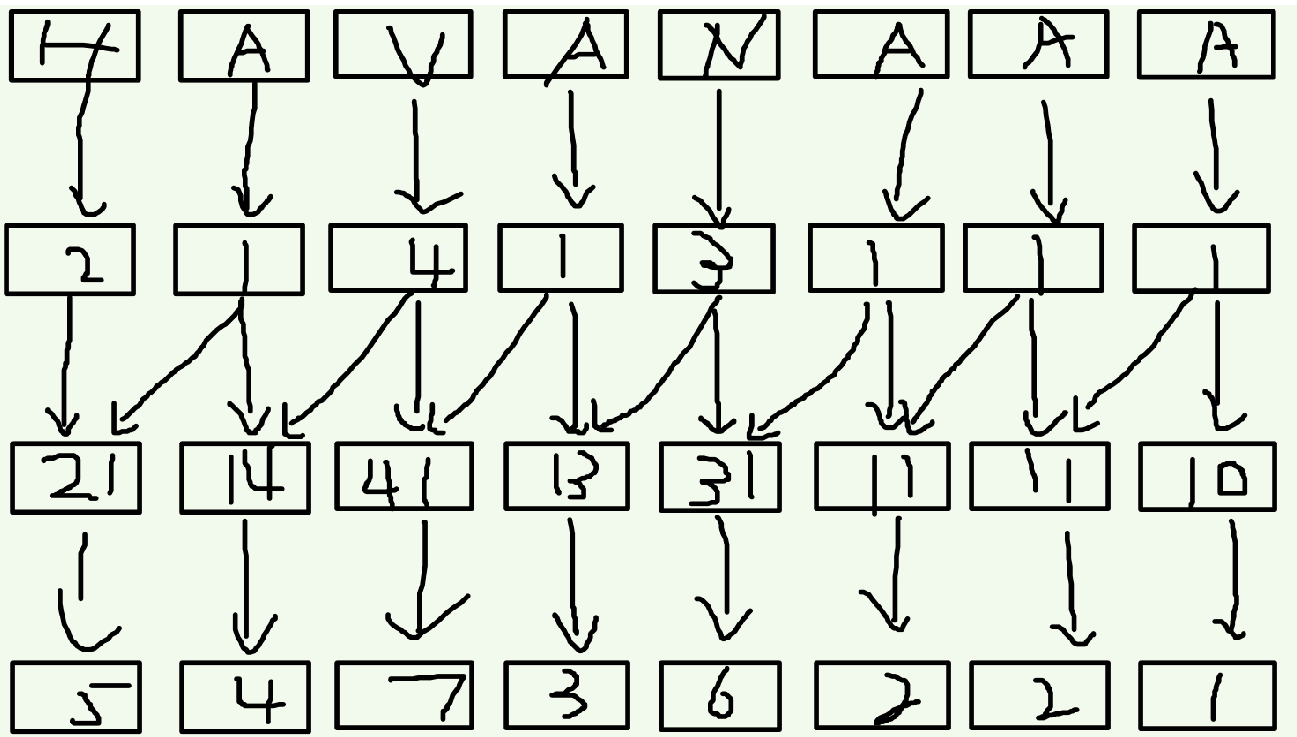
既然是倍增,就要有点倍增的样子。接下来我们对于一个在第 \(i\) 位上的关键字,它的第二关键字就是第 \(i+2\) 位置上的,联想一下,因为现在第 \(i\) 位上的关键字是 \(suff(i)\) 的前两个字符的排名,第 \(i+2\) 位置上的关键字是 \(suff(i+2)\) 的前两个字符的排名,这两个一合并,不就是 \(suff(i)\) 的前四个字符的排名吗?方法同上,排序之后重新标号,没有第二关键字的补零。同理我们可以证明,下一次我们要合并的是第 i 位和第 i+4 位,以此类推即可……

那么我们什么时候结束呢?很简单,当所有的排名都不同的时候我们直接退出就可以了,因为已经排好了。最多倍增 \(O(\log n)\) 次,使用 sort 排序,总复杂度 \(O(n \log^2 n)\)。
这种方法的常数远小于上一种方法, 因为倍增中每次排序都会使后缀数组更有序, sort 越有序跑得越快, 有序后可以提前退出, 所以跑不满 O(n \log^2 n) (代码)。
\(O(n \log n)\) 做法
复杂度还是一样, 复杂度瓶颈是倍增和排序好像也没啥变化, 除了常数变小, 这种做法还有什么好处吗?
当然有!排序的关键字变为了上一次排序的排名, 排名是 \(O(n)\) 的, 聪明的同学们应该立刻想到计数排序。关键字有两个也好办, 多关键字计数排序就是基数排序, 常数个关键字的基数排序时间复杂度还是 \(O(n)\), 排序两次就成了。
因为两次计数排序需要很多转换, 代码里很多层循环, 总复杂度是常数略大的 \(O(n \log n)\), 并没有与上面的小常数 \(O(n \log^2 n)\) 拉开太大差距。
\(O(n)\) 做法
还没有学,先在这里挖个坑,以后学了再补。
参考:
标签:字符,Suffix,后缀,复杂度,关键字,Array,排序,log From: https://www.cnblogs.com/xm-blog/p/18340581