这是一篇大量利用 STL 的题解。
1、题意转化
原题说了非常多的路径费用定义,不妨直接画图来研究一下:
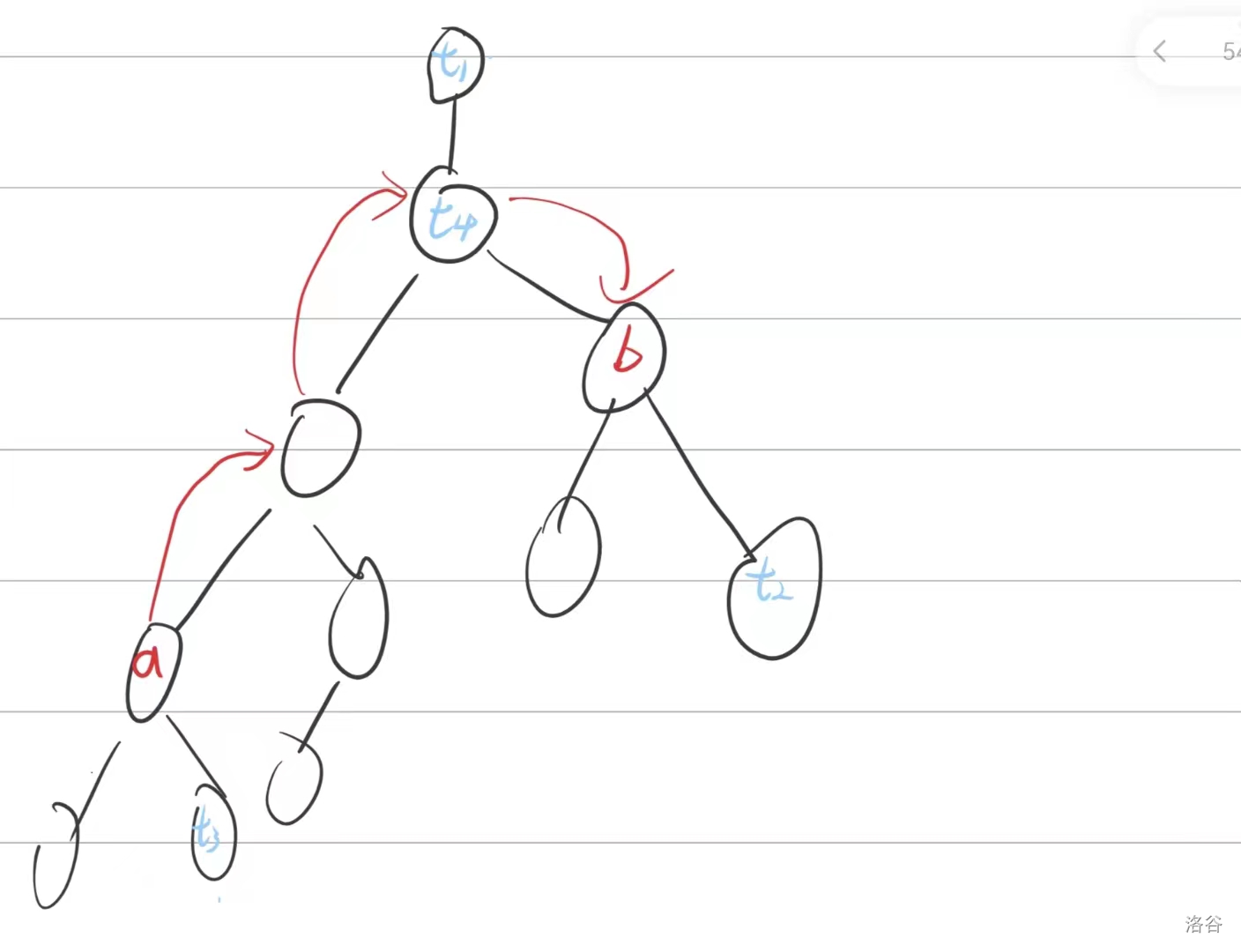
手摸一下可以发现,对于上图中 \(t_1\)、\(t_2\)、\(t_3\)、\(t_4\)四个点,所谓的 \(dis_{t,a}\) 与 \(dis_{t,b}\) 的异或值,不正是在 \(a\) 到 \(b\) 的路径上的挖掉一个点后的所有点权的总异或和吗?以 \(t_1\) 为例子,其到 \(a\) 与 \(b\) 的最近公共祖先 \(t_4\) 的这段路,在总答案的异或和中,其实是被异或了两次,即消去了。(不了解异或性质的可自行百度)。
那么,原问题其实可以转化为:询问树上的一对点,将其简单路径上挖去一个点(包括端点)的值,问是否可以使其总异或和为 \(k\)。
如果一个个暴力删除路径上的点,显然时间复杂度是不可能过得去的。正难则反,不妨如此考虑:路径总异或和 \(tot\) 和目标 \(k\) 其实是确定的,因此我们可以求出目标删除值为 \(d = tot ⨁ k\)。
现在,问题就转化了为求一段路径上是否有权值为 \(d\) 的点。
2、实现
对于路径总异或和,我们可以使用树链剖分与前缀和(或线段树)解决。如何查询是否存在权值 \(d\) 成为主要问题。
不妨考虑树链剖分的实现过程:每次选中一条链,将当前点跳到链顶,以此往复。需要注意的是,一条链中的点的 dfn 序是连续的。那这就给了我们一个思路。
首先,使用 map 对所有权值离散化。然后,对于每个权值,用 multiset 维护其对应的所有点的 dfn 序,以此存储所有权值所出现在的位置。
接下来就好办了。在树链剖分上跳的过程中,对目标权值的 multiset 进行二分查找,判断是否有对应的点存在当前这条链上即可。
3、注意事项
- 注意 \(LCA(a,b)\) 的权值其实被计算了两次,要将其补回来。
- 对 multiset 和 set 使用 lower_bound 或 upper_bound 函数时,因使用其自带的那种,不能使用头文件中的通用函数,否则时间复杂度会退化成 \(O(N)\)。
- 在树链剖分上跳之前直接求出目标值 \(d\) 的对应离散化编号,而不是边跳边求。否则时间复杂度也会退化,有可能导致超时。
上代码:
#include <bits/stdc++.h>
using namespace std;
#define N 1000010
#define ll long long
template <class T>
inline void read(T& a){
T x = 0, s = 1;
char c = getchar();
while(!isdigit(c)){ if(c == '-') s = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + (c ^ '0'); c = getchar(); }
a = x * s;
return ;
}
struct node{
int u, v;
ll w;
int next;
} t[N << 1];
int head[N];
int bian = 0;
inline void addedge(int u, int v, ll w){ // 双向边
t[++bian] = (node){u, v, w, head[u]}, head[u] = bian;
t[++bian] = (node){v, u, w, head[v]}, head[v] = bian;
return ;
}
int n, Q;
multiset <int> G[N];
ll a[N];
int dfn[N], top[N], son[N], siz[N], deth[N];
int fa[N], id = 0, rev[N];
ll sum[N]; // 树上前缀和数组
void dfs1(int u, int father){
deth[u] = deth[father] + 1;
siz[u] = 1;
fa[u] = father;
sum[u] = a[u] ^ sum[father];
int maxn = -1e9;
for(int i = head[u]; i; i = t[i].next){
int v = t[i].v;
if(v != father){
dfs1(v, u);
siz[u] += siz[v];
if(siz[v] > maxn){
maxn = siz[v];
son[u] = v;
}
}
}
return ;
}
void dfs2(int u, int tp){
top[u] = tp;
dfn[u] = ++id;
rev[id] = u;
if(!son[u]) return ;
dfs2(son[u], tp);
for(int i = head[u]; i; i = t[i].next){
int v = t[i].v;
if(v != fa[u] && v != son[u])
dfs2(v, v);
}
return ;
}
int LCA(int x, int y){ // 求 LCA
while(top[x] != top[y]){
if(deth[top[x]] < deth[top[y]]) swap(x, y);
x = fa[top[x]];
}
return deth[x] < deth[y] ? x : y;
}
int check(int x, int y, int d){ // 检查值
while(top[x] != top[y]){
if(deth[top[x]] < deth[top[y]]) swap(x, y);
auto l = G[d].lower_bound(dfn[top[x]]);
auto r = G[d].upper_bound(dfn[x]);
if(l != r) return 1;
x = fa[top[x]];
}
if(deth[x] < deth[y]) swap(x, y);
auto r = G[d].upper_bound(dfn[x]);
auto l = G[d].lower_bound(dfn[y]);
if(l != r) return 1;
return 0;
}
int hehe = 0;
map <int, int> g;
int main(){
// freopen("hh.txt", "r", stdin);
read(n), read(Q);
for(int i = 1; i <= n; i++){
read(a[i]);
if(!g.count(a[i])) g[a[i]] = ++hehe; // 离散化
}
for(int i = 1; i < n; i++){
int x, y;
read(x), read(y);
addedge(x, y, 0);
}
dfs1(1, 0);
dfs2(1, 1);
for(int i = 1; i <= n; i++){
G[g[a[i]]].insert(dfn[i]); // 插入点的值
}
while(Q--){
ll x, y, k;
read(x), read(y); read(k);
ll ans = sum[x] ^ sum[y];
int lca = LCA(x, y);
ans ^= a[lca];
ll d = ans ^ k; // d: 需要寻找的值
d = g[d]; // 提前找好编号
if(check(x, y, d)) puts("Yes");
else puts("No");
}
return 0;
}