全文链接:http://tecdat.cn/?p=29196
全文出处:拓端数据部落公众号
吸烟、喝酒和赌博被认为是由许多因素造成的。Logistic回归分析是一个非常有效的模型,可以检验各种解释变量和二元反应变量之间的关系。同时,双变量模型分析也被用于检验单变量模型之间的相关性。本项目的目的是利用统计方法来检验某个因素是否对吸烟、喝酒或赌博偏好有显著影响。然后用这个结果来预测这些习惯之间的组合。
绪论
本章介绍了 "解释吸烟喝酒和赌博的参与 "的研究背景。实际上,由于吸烟、喝酒和赌博的双重性和复杂性,它们的争论从未停止。大量的人把吸烟、喝酒和赌博当作坏习惯,有许多原因使他们反对这些习惯,许多研究也支持他们的观点。
文献回顾
涉及吸烟、饮酒和赌博习惯的关联的文献越来越多。在早期的研究中,许多研究者认为,吸烟、喝酒和赌博有明显的结合。每天吸烟的人比非每天吸烟的人更有可能参与赌博活动。每日吸烟者比非每日吸烟者在赌博上花费更多的时间和金钱(Nancy M. Petry和Cheryl Oncken,2002)。
方法论
模型假设
从数据集来看,吸烟、喝酒和赌博的反应显然只有是或不是,这是二进制的。而且,所有的解释因素都可以被归类或被视为连续的。因此,使用Logistic回归作为基本模型是可靠的。

基础知识。Logistic回归可以是二元的,也可以是多元的。在二进制中,结果只能是0或1,而在多进制中,结果可以是三个或更多,例如,A、B和C三个级别。
Logistic函数是

然后

如果有多个解释变量,上述表达式β0+β1x可以修改为β0+β1x1+β2x2+...。+ βmxm。在这种情况下,我们假设:Y1=吸烟,Y2=喝酒,Y3=赌博。我们有8个解释者,每个解释者可以分为几个类别。因此
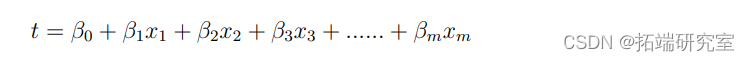
和

其中i = 1, 2, 3
那么,如果吸烟,y1=1,否则y1=0。
y2 = 1,如果喝酒,y2 = 0,否则。
y3=1,如果赌博,y3=0,否则。
此外,随机效应也应该被添加到模型中。
带随机效应的Logistic回归

分析数据
以下显示了我们如何进行这项研究。首先,我们参考文献和以前所做的研究,以确定那些被认为对吸烟、喝酒和赌博有重大影响的潜在变量。
结果
在这一部分中,我们将对单一分类的解释因素进行分析。首先,将使用箱形图来显示连续变量与吸烟、饮酒和赌博等的关联。箱形图将显示连续变量与Yi的关系。同时,条形图将被用来显示分类变量的影响。
吸烟结果
- ggplot(smoke_age,aes(as.factor(smoking),age))+
- geom_boxplot()+labs(title="Smoking-age",x="smoking",y="age")


从图1可以看出,吸烟者的年龄中位数比非吸烟者小。吸烟者的年龄段在18至87岁之间,而非吸烟者则分布在各个年龄段。该图表明,年轻人更有可能吸烟。年龄对吸烟有明显的影响,年龄的估计值为-0.1017,这意味着吸烟和年龄有负相关。
- ggplot(smoke_gender, aes(gender,fill=as.factor(smoking)))+
- geom_bar(position = "fill")+
- labs(title ="Smoking-gender", x = "gender", y = "smoking")


参照图2,1代表吸烟者,0代表不吸烟者。图中显示,男性吸烟者比女性吸烟者多一点,这意味着性别对吸烟偏好有影响。R输出也给出了同样的结论,P值是显著的,男性的估计值为0.20793,这意味着男性更可能吸烟。
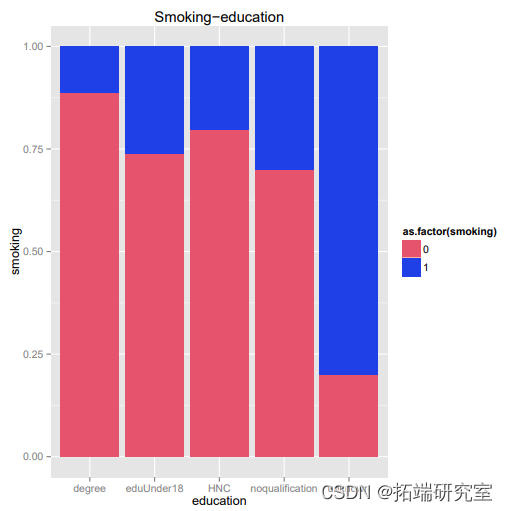

图3表明,教育水平对吸烟习惯有显著影响。吸烟的概率按照教育水平的顺序排列。拥有较高教育水平的人吸烟的可能性较小。尽管数据不详,但很明显,拥有学位的人最不可能吸烟,而没有学历的人最可能吸烟。HNC组的吸烟者比EDU-18以下组少。图4右侧的估计值与图中的数据相符。随着教育水平的提高,吸烟者的概率明显下降。吸烟的概率与教育水平呈负相关。
带有随机效应的单变量模型
检查随机效应的显著性
fit.no < −glm(gambler 1, f amily = binomial(logit0))
And check significance using
anova(f it.ID, f it.no)
在'fit.no'中加入随机效应后,AIC从1269.5降低到895.3,P值显示了家庭ID的显著影响。因此,在单变量模型中加入随机效应是合理的。
使用'lme4'拟合单变量模型
在这一节中,吸烟、喝酒和赌博的数据将在单变量模型中被拟合。以下是来自R的结果。
re.smoker=glmer(smoker~male+age+income+whiteO+mixed+asian+chinese+african+other+degresummary(re.smoker)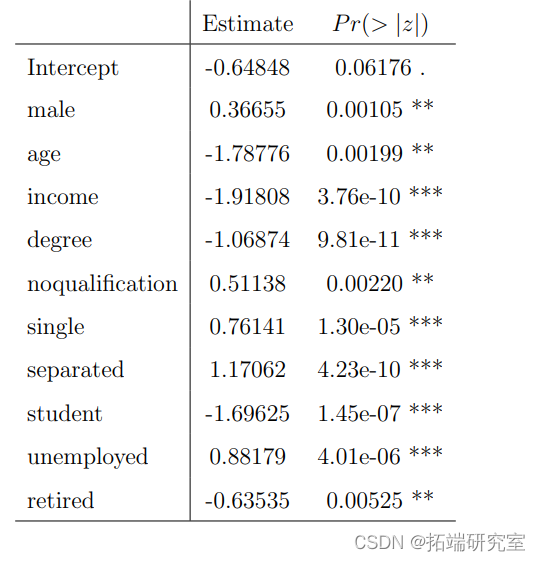
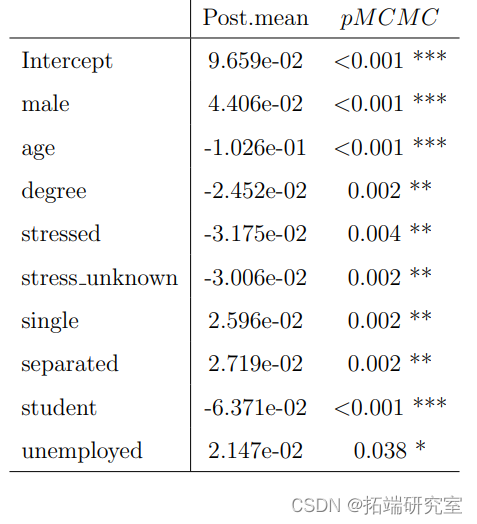
表2包含对吸烟偏好有明显影响的变量。可以得出结论:男性、年轻、收入低、无学历、单身、分居或失业的人更有可能成为吸烟者。而女性、年龄较大、收入较高、有学位、学生或退休的人则不太可能成为烟民。饮酒模型也有和吸烟模型一样的问题,所以我们也需要放弃一些列以确保模型能够收敛。

以上是本项目中的单变量模型,每个模型都已经分析过了,接下来我们将使用这些单变量模型来拟合双变量模型。
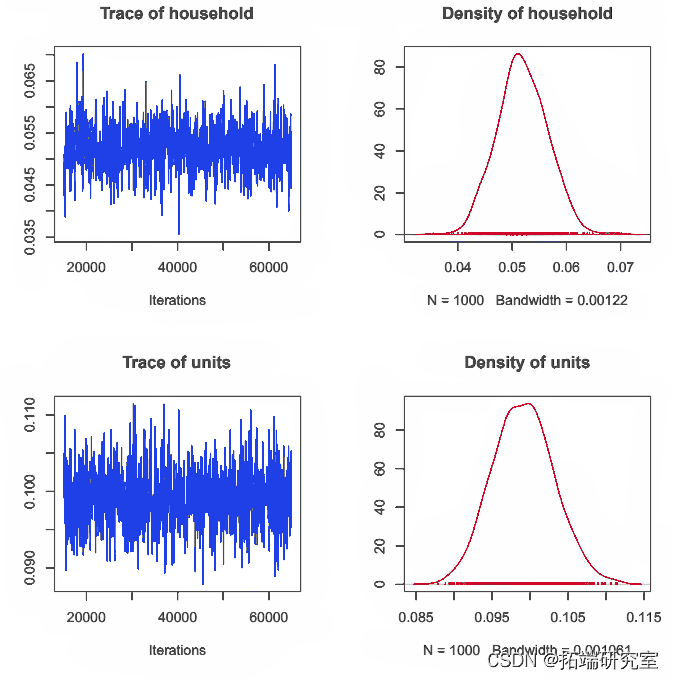
使用 "MCMCglmm "拟合单变量模型
由于每个单变量模型都是由一系列因素拟合的,为了了解反应是如何相互影响的,我们可能还要考虑到与其他性状可能存在的协方差。
model.smoker<- MCMCglmm(smoker~male+age+income+whiteO+mixed+asian+chinese+african+arasummary(model.smoker)
表5中的显著变量与表2非常相似,唯一不同的是,被放弃的变量 "edu unknown "和 "employother "在表5中是显著变量。

从表6和表3可以看出,使用'lme4'和'MCMCglmm'的饮酒模型预测了相同的显著效果。

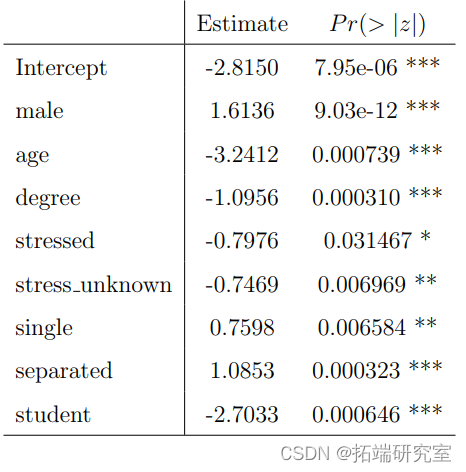
与表7和表4相比,大多数重要的变量是相同的,只有 "失业 "在使用 "lme4 "的赌博模型中不显著。
使用'MCMCglmm'的双变量模型
在本节中,我们将计算出本项目的最终结果,即吸烟、喝酒和赌博习惯之间的关系。
在这里,我们可以计算出吸烟者和饮酒者之间的相关关系,其方差为




相关性=posterior.mode(correlation) = 0.16
正相关表明,在这个双变量模型中,喜欢吸烟的人更可能是饮酒者。
在分析了吸烟者和饮酒者之间的相关性之后,我们现在用双变量的'MCMCglmm'模型来测试吸烟者和赌博者之间的关系船。表9显示了单变量模型的协变量。
启示
通过使用逻辑回归法,我们能够确定导致吸烟、喝酒和赌博的重要因素。在本项目中,似乎对这三种习惯都有影响的重要因素是性别、教育水平和婚姻状况。同时,本研究还给出了每个分类因素的估计值,这可以用来说明某个因素对这些习惯的影响是积极的还是消极的。
吸烟、饮酒和赌博之间的组合是通过双变量模型来检验的。利用这个模型,我们可以得到吸烟模型、饮酒模型和赌博模型之间的固定和随机效应的相关关系。例如,通过正相关关系,我们可以说明喜欢吸烟的人也会喜欢喝酒。
References
Kenneth J.Mukamal. The effects of smoking and drinking on cardiovascular disease and risk factors. Alcohol Research & Health Vol. 29, No. 3, 2006
William J. Blot, Joseph K. McLaughlin, Deborah M. Winn, et al. 吸烟和饮酒与口腔和咽喉癌的关系. 癌症研究》1988;48:3282-3287。

最受欢迎的见解
3.matlab中的偏最小二乘回归(PLSR)和主成分回归(PCR)
6.r语言中对LASSO回归,Ridge岭回归和Elastic Net模型实现
7.R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
9.R语言用逻辑回归、决策树和随机森林对信贷数据集进行分类预测
标签:吸烟者,MCMC,变量,lme4,回归,吸烟,Logistic,赌博,模型 From: https://www.cnblogs.com/tecdat/p/16815904.html