用一个长度为 N 的整数数组 A ,描述山峰和山谷的高度。山峰需要满足如下条件, 0<P<N−1 且 A[P−1]<A[P]>A[P+1] 。
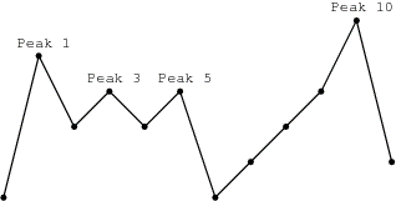
以本图为例,高度为: 1 5 3 4 3 4 1 2 3 4 6 2 。其中可以作为山峰的点为: 1 3 5 10 。
放 2 面旗子, 可以放在 1 和 5 。
放 3 面旗子, 可以放在 1 5 和 10 。
放 4 面旗子, 可以放在 1 5 和 10 ,之后就放不下了。
所以最多可以放 3 面旗子。
Input
第 1 行:一个数 N ,表示数组的长度 (1≤N≤50000) 。
第 2∼N+1 行:每行 1 个数 Ai(1≤Ai≤109) 。
Output
输出最多能插上多少面旗子(即求 K 的最大值)。
Sample 1
| Inputcopy | Outputcopy |
|---|---|
| 12 | |
| 1 | |
| 5 | |
| 3 | |
| 4 | |
| 3 | |
| 4 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 6 | |
| 2 | 3 |
思路
先统计是山峰的点
code
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
int n, m;
const int N = 5e4 + 5;
int num[N], peak[N];//peak存入山峰的点
int k = 0;//山峰个数
bool check(int x){
//第一个山峰肯定要插旗子
int prev = peak[0];//prev先初始化为第一个山峰点
int cnt = 0;//记录所插旗子个数
for(int i = 1; i < k; i++){
int pos = peak[i];
if(pos - prev >= x){
cnt++;
prev = pos;
}
}
return cnt >= x - 1;
}
int main() {
cin >> n;
for (int i = 0; i < n; ++i) {
cin >> num[i];
}
for (int i = 1; i < n - 1; ++i) {
if(num[i] > num[i - 1] && num[i] > num[i + 1]){
peak[k++] = i;
}
}
if(k == 0){
cout << 0;
return 0;
}
if(k == 1){
cout << 1;
return 0;
}
//二分旗子个数
int result = 0;
int l = 2, r = k;
while(l <= r){
int mid = (l + r) >> 1;
if(check(mid)){
result = mid;
l = mid + 1;
}else{
r = mid - 1;
}
}
cout << result;
return 0;
}