首页 > 其他分享 >【离线】- 莫队

【离线】- 莫队

时间：2024-07-19 09:22:03浏览次数：8  
标签：int 离线 tot ++ -- now 莫队

前言

莫队是由莫涛提出的一种离线算法，是分块与双指针的结合，一般可以在 \(O(n \sqrt n)\) 或者 \(O(n \sqrt m)\) 的复杂度解决一些种类问题。

普通莫队

SP3267 DQUERY - D-query

给你一个长度为 \(n\) 的数列 \(A\)，\(m\) 次询问，每次询问区间 \([l,r]\) 内的不同数字的个数。

如果要在线的话，需要用主席树。

我们考虑离线，把每个操作离线下来，然后挂到序列上。

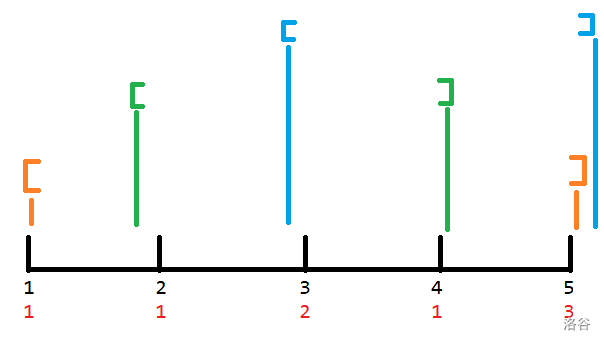
每一个颜色代表一个询问。

可以想到用双指针来做，代表区间 \([l, r]\)，如果任意指针移动就更新答案，是 \(O(1)\) 的。

想象是美好的，现实是残酷的。

如果询问是这样子的话：

那么尽管排完序左端点的移动可以做到 \(O(n)\)，但是啊但是，右端点是无序的，就又会把复杂度打会 \(O(nm)\)。

那么这时候，莫队诞生了。

莫队在原来的基础上加了一个分块与排序。

可以证明复杂度是 \(O(n\sqrt n)\) 的。

对于左端点，如果每一个块中有 \(x\) 个询问的左端点，那么对于这个块的最坏复杂度是 \(O(x_i\sqrt n)\)。对于整个块，跨越一次需要 \(O(\sqrt n)\)，最坏会跨整个序列，也就是 \(O(n)\)，那么复杂度就是 $ O (\sum x_i\sqrt n + n\sqrt n) = O (n \sqrt n)$。

对于右端点，因为已经排完序，最坏需要跨整个序列，也就是 \(O(n)\)，有 \(O(\sqrt n)\) 块，所以复杂度就是 \(O(n \sqrt n)\)。

所以总复杂度就是 \(O(n \log n + n \sqrt n + n \sqrt n) = O(n \sqrt n)\)。

回到这题，我们已经可以基本写出来了。

int n, m, len, tot;
int a[N], cnt[V];

bool cmp (Query A, Query B) { return A.x / len == B.x / len ? (A.y == B.y ? 0 : ((A.x / len) & 1) ^ (A.y < B.y)) : A.x < B.x; }
bool Cmp (Query A, Query B) { return A.id < B.id; } // 这里用了两个 cmp，实际不需要，用一个 ans 数组记录即可。

// 移动指针的修改
void add (int x) {
	if (!cnt[a[x]]) tot++;
	cnt[a[x]]++;
}

void del (int x) {
	if (cnt[a[x]] == 1) tot--;
	cnt[a[x]]--;
}

int main () {
	
	len = sqrt (n); // 这句话千万别漏了
	sort (q + 1, q + m + 1, cmp);
	
	for (int i = 1, l = 1, r = 0; i <= m; ++i) {
		while (l > q[i].x) add (--l);
		while (r < q[i].y) add (++r);
		while (l < q[i].x) del (l++);
		while (r > q[i].y) del (r--);
		
		q[i].ans = tot;
	}
	
	sort (q + 1, q + m + 1, Cmp);
  
	return 0;
}

带修莫队

毫不废话，上题。

P1903 [国家集训队] 数颜色 / 维护队列

给你一个长度为 \(n\) 的序列 \(A\) 以及 \(m\) 个操作，要你支持单点修改，并且询问区间颜色种类数。

现在带修了，如何是好？

我们不妨把每一个操作用时间戳来表示，这样我们就可以多一个维度 \(t\)，用来记录每次询问的时间维度。

初始化时，只需要找到最近的那个时间维度即可。

再来考虑考虑这个维度该怎么转移。

我们假设当前这个区间已经修改了 \(x\) 次，要转移到修改 \(y\) 次的序列。

如果 \(x \lt y\)，那么我们需要把 \(x + 1\) 到 \(y\) 个修改全都加上。

如果 \(x \gt y\)，那么我们需要把 \(x\) 到 \(y + 1\) 个修改全部还原。

什么？你问 \(x = y\)？

这种情况还需要转移吗。。。

于是我们在原来莫队的基础上加了一维，成功地实现了带修莫队。

int n, m, len, qcnt, rcnt;
int a[N], ans[N], cnt[V], tot;

struct Query {
	int id, l, r, t;
	
	bool operator < (const Query &T) {
		if (l / len != T.l / len) return l < T.l;
		if (r / len != T.r / len) return r < T.r;
		return t < T.t;
	}
} q[N];

void add (int x) {
	if (!cnt[x]) tot++;
	cnt[x]++;
}

void del (int x) {
	if (cnt[x] == 1) tot--;
	cnt[x]--;
}

int main () {

	for (int i = 1; i <= m; ++i) {
		char opt;
		int x, y;
		cin >> opt >> x >> y;
		
		if (opt == 'Q') q[++qcnt] = (Query){qcnt, x, y, rcnt};
		else r[++rcnt] = (Modify){x, y};
	}
	
	len = pow (n, 2.0 / 3.0);
	
	int L = 1, R = 0, now = 0;
	sort (q + 1, q + qcnt + 1);
	for (int i = 1; i <= qcnt; ++i) {
		while (L > q[i].l) add (a[--L]);
		while (R < q[i].r) add (a[++R]);
		while (L < q[i].l) del (a[L++]);
		while (R > q[i].r) del (a[R--]);
		while (now < q[i].t) {
			now++;
			if (L <= r[now].x && r[now].x <= R) {
				add (r[now].y);
				del (a[r[now].x]);
			}
			swap (a[r[now].x], r[now].y);
		}
		while (now > q[i].t) {
			if (L <= r[now].x && r[now].x <= R) {
				add (r[now].y);
				del (a[r[now].x]);
			}
			swap (a[r[now].x], r[now].y);
			now--;
		}
		
		ans[q[i].id] = tot;
	}
	
	return 0;
}

树上莫队

众所周知，莫队是用于序列上的一种算法，如果要用到树上，我们最先想到的就是把树序列化。

假树上莫队

但是一般的 DFS 序这样肯定是不行的，毕竟要方便统计路径上权值的种类数。

但是欧拉序很好的满足了这个要求。

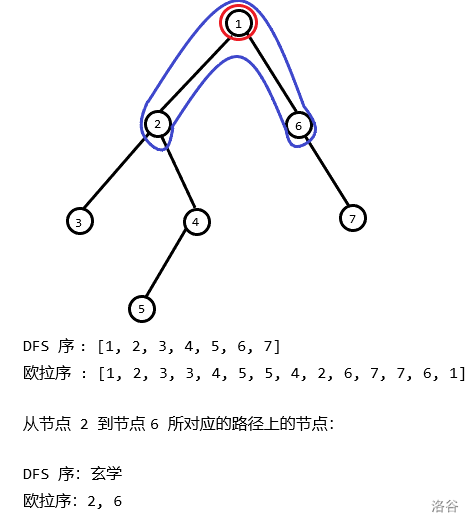
如图，可以发现欧拉序只有标红圈的节点没有算上，而这个标红圈的节点正是 \(2\) 与 \(6\) 的 Lca。

所以我们只需要在转移过程中特判一下即可。

SP10707 COT2 - Count on a tree II

给你一棵 \(n\) 个节点的树，每次询问路径 \(u\) 到 \(v\) 上的权值种类数。

典，直接上。

const int N = 2e5 + 5;
int n, m, len; 

int dep[N], fa[N][31], lg[N], eu[N], ucnt;
int fi[N], ls[N];

void dfs (int now, int fath){
    fa[now][0] = fath;
    dep[now] = dep[fath] + 1;
    eu[++ucnt] = now;
    fi[now] = ucnt;

    for (int i = 1; i < 31; ++i){
        fa[now][i] = fa[fa[now][i-1]][i-1];
    }
    for (int i = head[now]; i; i = e[i].nxt)
        if (e[i].v != fath)
            dfs(e[i].v, now);
    
    eu[++ucnt] = now;
    ls[now] = ucnt;
}

int Lca (int x, int y)

void modify (int x) {
	if (!vis[x]) {
		if (!cnt[a[x]]) tot++;
		cnt[a[x]]++;
	} else {
		if (cnt[a[x]] == 1) tot--;
		cnt[a[x]]--;
	}
	
	vis[x] ^= 1;
}

int main () {
	
	ios::sync_with_stdio (false);
	cin.tie (0); cout.tie (0);
	
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
		b[i] = a[i];
	}
	for (int i = 1; i < n; ++i) {
		int u, v;
		cin >> u >> v;
		addEdge (u, v);
		addEdge (v, u);
	}
	
	sort (b + 1, b + n + 1);
	int ret = unique (b + 1, b + n + 1) - b - 1;
	for (int i = 1; i <= n; ++i) a[i] = lower_bound (b + 1, b + n + 1, a[i]) - b;
	
	len = sqrt (n);
	
	for (int i = 1; i <= m; ++i) {
		int x, y;
		cin >> x >> y;
		
		if (fi[x] > fi[y]) swap (x, y);
		q[i].id = i, q[i].lca = Lca (x, y);
		
		if (q[i].lca == x) {
			q[i].x = fi[x];
			q[i].y = fi[y];
			q[i].lca = 0;
		} else {
			q[i].x = ls[x];
			q[i].y = fi[y];
		}
	}
	
	sort (q + 1, q + m + 1);
	
	int l = 1, r = 0;
	for (int i = 1; i <= m; ++i) {
		while (l > q[i].x) modify (eu[--l]);
		while (r < q[i].y) modify (eu[++r]);
		while (l < q[i].x) modify (eu[l++]);
		while (r > q[i].y) modify (eu[r--]);
		if (q[i].lca) modify (q[i].lca); // 注意特判
		ans[q[i].id] = tot;
		if (q[i].lca) modify (q[i].lca);
	}
	return 0;
}

真树上莫队

这玩意需要考虑到指针的移动啊，翻转啊等等，但是由于我实在是太懒了不可控因素，所以下次一定~

拓展 - 莫队 + 值域分块

你知道吗，其实莫队可以做这道题。

P3380 【模板】树套树

给你一个长度为 \(n\) 的有序数列，需要你实现区间内查询排名，第 \(k\) 小，单点修改，前驱，后继。

这玩意就是 wzykhp123 成莫队之神的原因。

行，废话不多说。

值域分块

对于这种处理对象在序列上的问题，我们依然可以使用莫队解决。但是对于每一个询问，为了保证算法不带 log的优越性，我们仍然需要一种根号算法。

也就是所谓的值域分块，需要离散化。

值域分块专门针对于这种 \(k\) 小问题。

那么了解这个玩意后，其实就可以写了。但是细节有点多，要做好调试的准备。

const int N = 1e5 + 5;

int n, m, len, Len, tot, Cnt;
int a[N], A[N << 1];

int cnt[N], ans[N];  
int bel[N], num[N], l[N], r[N];

int qcnt, rcnt;

void add (int x) {
	cnt[x]++;
	num[bel[x]]++;
}

void del (int x) {
	cnt[x]--;
	num[bel[x]]--;
}

int getrnk (int k) {
	int rnk = 1;
	for (int i = 1; i <= Cnt; ++i) {
		if (k <= r[i]) for (int j = l[i]; j < k; ++j) rnk += cnt[j];
		else rnk += num[i];
	}
	
	return rnk;
}

int getkth (int k) {
	for (int i = 1; i <= Cnt; ++i) {
		if (k <= num[i]) {
			for (int j = l[i]; j <= r[i]; ++j) {
				k -= cnt[j];
				if (k <= 0) return A[j];
			}
		} else k -= num[i];
	}
	return -1;
}

int getpre (int k) {
	int rnk = getrnk (k);
	if (rnk == 1) return -2147483647;
	return getkth (rnk - 1);
}

int getbk (int k) {
	int rnk = getrnk (k);
	if (rnk == -1) return 2147483647;
	int ret;
	if (cnt[k] > 0) ret = getkth (rnk + 1); // 注意这里，如果 k 出现在序列里面的话...
	else ret = getkth (rnk);
	
	if (ret == -1) return 2147483647;
	return ret;
}

void write (int x) {
	if (x < 0) putchar ('-'), x = -x;
	if (x > 9) write (x / 10);
	putchar (x % 10 + '0'); 
}

int main () {
	
	ios::sync_with_stdio (false);
	cin.tie (0);
	
	cin >> n >> m;
	len = pow (n, 2.0 / 3.0);
	
	for (int i = 1; i <= n; ++i) {
		cin >> a[i];
		A[++tot] = a[i];
	}
	
	for (int i = 1; i <= m; ++i) {
		int opt;
		cin >> opt;
		
		if (opt == 3) {
			rnum++;
			cin >> mod[rnum].x >> mod[rnum].y;
			A[++tot] = mod[rnum].y;
		} else {
			qnum++;
			q[qnum].opt = opt;
			q[qnum].t = rnum;
			q[qnum].id = qnum;
			cin >> q[qnum].x >> q[qnum].y >> q[qnum].k;
			A[++tot] = q[qnum].k;
		}
	}
	sort (q + 1, q + qcnt + 1);
	
	
	sort (A + 1, A + tot + 1);
	tot = unique (A + 1, A + tot + 1) - A - 1;
	for (int i = 1; i <= n + rnum + qnum; ++i) {
		if (i <= n) a[i] = lower_bound (A + 1, A + tot + 1, a[i]) - A;
		else if (i <= n + rnum) mod[i - n].y = lower_bound (A + 1, A + tot + 1, mod[i - n].y) - A;
		else if (q[i - n - rnum].opt != 2) q[i - n - rnum].k = lower_bound (A + 1, A + tot + 1, q[i - n - rnum].k) - A;
		
	}
	
	Len = sqrt (tot);
	Cnt = tot / Len;
	
	for (int i = 1; i <= tot; ++i) bel[i] = (i - 1) / Len + 1;
	for (int i = 1; i <= Cnt; ++i) {
		l[i] = (i - 1) * Len + 1;
		r[i] = i * Len;
	}
	
	if (r[Cnt] < tot) {
		Cnt++;
		l[Cnt] = r[Cnt - 1] + 1;
		r[Cnt] = tot;
	} 
	
	int L = 1, R = 0, now = 0;
	for (int i = 1; i <= qnum; ++i) {
		while (L > q[i].x) add (a[--L]);
		while (R < q[i].y) add (a[++R]);
		while (L < q[i].x) del (a[L++]);
		while (R > q[i].y) del (a[R--]);
		while (now < q[i].t) {
			now++;
			if (L <= mod[now].x && mod[now].x <= R) {
				add (mod[now].y);
				del (a[mod[now].x]);
			}
			swap (a[mod[now].x], mod[now].y);
		}
		while (now > q[i].t) {
			if (L <= mod[now].x && mod[now].x <= R) {
				add (mod[now].y);
				del (a[mod[now].x]);
			}
			swap (a[mod[now].x], mod[now].y);
			now--;
		}

		if (q[i].opt == 1) ans[q[i].id] = getrnk (q[i].k);
		if (q[i].opt == 2) ans[q[i].id] = getkth (q[i].k);
		if (q[i].opt == 4) ans[q[i].id] = getpre (q[i].k);
		if (q[i].opt == 5) ans[q[i].id] = getbk (q[i].k);
	}
  
	return 0;
}

标签：int,离线,tot,++,--,now,莫队
From： https://www.cnblogs.com/Xeanin/p/18310767

相关文章

  • 百度人脸识别Windows C++离线sdk C#接入
    百度人脸识别WindowsC++离线sdkC#接入目录说明设计背景•场景特点：•客户特点：•核心需求：SDK包结构效果代码说明自己根据SDK封装了动态库，然后C#调用。功能接口设计背景•场景特点：--网络：对于无网、局域网等情况，无法连接公网，API方式无法运作。如政府单......
  • 带修莫队模板
    取分块大小\(n^\frac{2}{3}\)最优。例题：数颜色#include<bits/stdc++.h>usingnamespacestd;usingi64=longlong;constintN=1e6+5;intcnt[N],a[N];structquery{intl,r,t,id;//加入时间戳};structmodfiy{intpos,val;};intmain(......
  • 莫队模板
    #include<bits/stdc++.h>usingnamespacestd;usingi64=longlong;constintN=1e6+5;intcnt[N],a[N];structquery{intl,r,id;};intmain(){ios::sync_with_stdio(false);cin.tie(nullptr);intn;cin>>n;......
  • 安装docker在线和离线方式
    1、添加阿里云的yum下载源yuminstall-yyum-utilsyum-config-manager--add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo#查看这个新加的yum源中有那些版本包配置yumlistdocker-ce--showduplicates|sort-r#下载安装需要的rpm包yuminstall......
  • 大数据之路 读书笔记 Day6 离线数据开发之数据开发平台
    回顾Day5数据同步遇到的问题与解决方案Day4数据同步1.统一计算平台1.1MaxCompute概述MaxCompute（原名ODPS，OpenDataProcessingService）是阿里云提供的一种快速、完全托管的EB级数据仓库解决方案。它为用户提供了海量数据存储和实时计算的能力，适用于离线数据处理......
  • ubuntu20.04离线部署ceph集群
    版本兼容：查看ceph和系统的版本是否兼容节点说明ceph-admin:192.168.83.133ceph节点IPDomainHostnameServices192.168.83.133stor01.kb.cxceph01mon,mgr,mds192.168.83.134stor02.kb.cxceph02mgr,mon,mds192.168.83.135stor03.kb.cxceph03osd,m......
  • Kubernetes高可用集群二进制离线部署（Runtime Docker）
    Kubernetes高可用集群二进制部署（RuntimeDocker）Kubernetes（简称为：k8s）是Google在2014年6月开源的一个容器集群管理系统，使用Go语言开发，用于管理云平台中多个主机上的容器化的应用，Kubernetes的目标是让部署容器化的应用简单并且高效,Kubernetes提供了资源调度、部署管理、服务......
  • CF1864F Exotic Queries （离线+线段树+树状数组）
    CF1864FExoticQueries离线+线段树+树状数组先把权值在\([l,r]\)之内的单独拎出来看性质。可以知道策略一定是元素从小到大消成\(0\)。当消除元素\(x\)时，最好的情况当然是一次全消了，但一般元素\(x\)的位置两两之间会有之前消成的\(0\)，将所有位置分成了\(n\)段，那么消......
  • 纯小白uni-app+Android Studio离线打包
    一、HBulderX（1）cloud：开发者中心 注册登录（2）HBulderX登录开发者中心的账号，创建uni-app项目-》test，此时点击test下文件mainfest.json，会出现如下uni-app的AppID 同时在CLOUD上也会出现此项目，注意，项目名称和AppID要对上 （3）HBulderX本地打包 打包结果如下，期间要下什么插件，就让......
  • 如何快速批量的下载贝壳看房VR全景图到本地电脑，实现离线浏览VR全景漫游，一招教会你
    无论你是专业摄影师、3D家装设计师，还是房产销售人员，经常会需要保存VR全景平台上的720全景图片到本地。直接用浏览器另存为常常无效，这时一款专门的全景图下载工具软件就派上用场了。轻松保存超清VR全景图片市面上有很多720全景图下载工具，但哪一款功能最强呢？我们推荐KD全景下......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99