数据结构第二阶段综合应用算法训练自选题,我选择的是文件压缩解压。
一、问题描述:
名称:基于哈夫曼编码的文件压缩解压
目的:利用哈夫曼编码压缩存储文件,节省空间
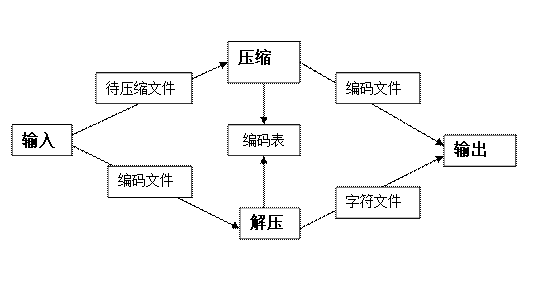
输入:任何格式的文件(压缩)或压缩文件(解压)
输出:压缩文件或解压后的原文件
功能:利用哈夫曼编码压缩解压文件
性能:快速
为了建立哈夫曼树,首先扫描源文件,统计每类字符出现的频度(出现的次数),然后根据字符频度建立哈夫曼树,接着根据哈夫曼树生成哈夫曼编码。再次扫描文件,每次读取8bits,根据“字符—编码”表,匹配编码,并将编码存入压缩文件,同时存入编码表。解压时,读取编码表,然后读取编码匹配编码表找到对应字符,存入文件,完成解压。
压缩解压的第一步就是读取文件,为了能够处理任何格式的文件,采用二进制方式读写文件。以一个无符号字符(unsigned char)的长度8位为处理单元,最多有256(0~255)种组合,即256类字符。
要建立哈夫曼树,先要得到各类字符的频度,我想到了两种扫描方案:
1、利用链表存储,每扫描到一类新字符就动态分配内存;
2、利用数组,静态分配256个空间,对应256类字符,然后用下标随机存储。
链表在需要时才分配存储空间,可以节省内存,但是每加入一个新字符都要扫描一次链表,很费时;考虑到仅有256个字符种类,不是很多,使用静态数组,不会造成很大的空间浪费,而可以用数组的下标匹配字符,不需扫描数组就可以找到每类字符的位置,达到随机存储的目的,效率有很大的提高。当然,不一定每类字符都出现,所以,统计完后,需要排序,将字符频度为零的结点剔除。
我定义的数组类似这样:Node array[CHAR_KINDS],其中CHAR_KINDS为8位无符号字符对应的256(0~255)种不同组合,这样每扫描到一个字符,直接将字符作为下标,就可以找到字符的位置。
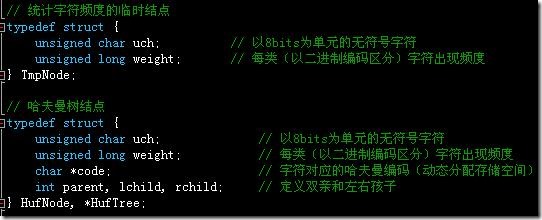
哈夫曼树为二叉树,树结点含有权重(在这里为字符频度,同时也要把频度相关联的字符保存在结点中)、左右孩子、双亲等信息。
考虑到建立哈夫曼树所需结点会比较多,也比较大,如果静态分配,会浪费很大空间,故我们打算用动态分配的方法,并且,为了利用数组的随机访问特性,也将所需的所有树节点一次性动态分配,保证其内存的连续性。另外,结点中存储编码的域,由于长度不定,也动态分配内存。
将其定义成临时结点TmpNode,这个结点仅保存字符及对应频度,也用动态分配,但是一次性分配256个空间,统计并将信息转移到树结点后,就将这256个空间释放,既利用了数组的随机访问,也避免了空间的浪费。
每类字符对应一串编码,故从叶子结点(字符所在结点)由下往上生成每类字符对应的编码,左‘0’,右‘1’。为了得到正向的编码,设置一个编码缓存数组,从后往前保存,然后从前往后拷贝到叶子结点对应编码域中,根据上面“建立哈夫曼树的协商”的约定,需要根据得到的编码长度为编码域分配空间。对于缓存数组的大小,由于字符种类最多为256种,构建的哈夫曼树最多有256个叶子结点,树的深度最大为255,故编码最长为255,所以分配256个空间,最后一位用于保存结束标志。
上面协定以8位的字符为单元编码,这里压缩当然也以8位为处理单元。
首先将字符及种类和编码(编码表)存储于压缩文件中,供解压时使用。
然后以二进制打开源文件,每次读取一个8位的无符号字符,循环扫描匹配存储于哈夫曼树节点中的编码信息。
由于编码长度不定,故需要一个编码缓存,待编码满足8位时才写入,文件结束时缓存中可能不足8位,在后面补0,凑足8位写入,并将编码的长度随后存入文件。
在哈夫曼树节点中,编码的每一位都是以字符形式保存的,占用空间很大,不可以直接写入压缩文件,故需要转为二进制形式写入;至于如何实现,可以定义一个函数,将保存编码的字符数组转为二进制,但是比较麻烦,效率也不高;正好,可以利用C语言提供的位操作(与、或、移位)来实现,每匹配一位,用“或”操作存入低位,并左移一位,为下一位腾出空间,依次循环,满足8位就写入一次。


两个重要的结点结构体:
三个函数用于建立哈夫曼树和生成哈夫曼编码:
两个主要函数——压缩解压函数:
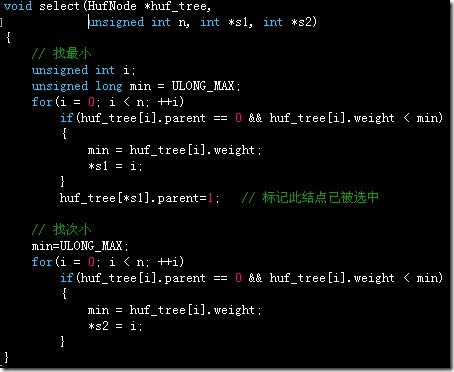
Select函数供CreateTree函数调用,找两个最小的结点,找到第一个后需要将其parent设为‘1’(初始化后为‘0’)表明此结点已被选中:
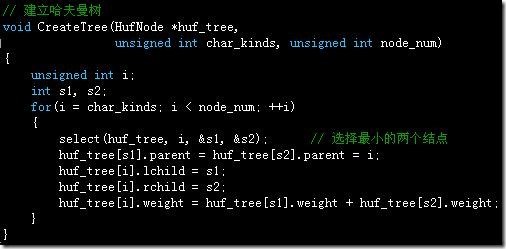
建立哈夫曼树,每次用select()函数找两个最小结点:
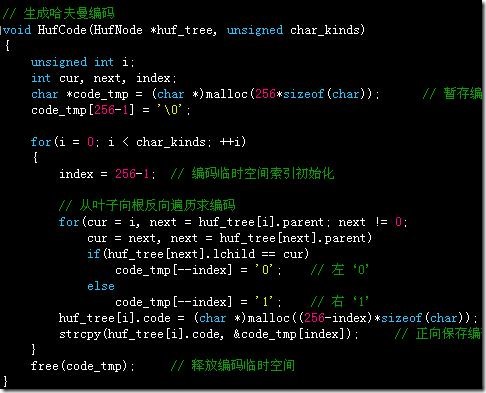
生成哈夫曼编码,由叶子到根反向生成编码,左‘0’,右‘1’,每个code域的内存动态分配:
标签:总结,字符,结点,哈夫曼,编码,小学,解压,第二周,256 From: https://www.cnblogs.com/binglinll/p/18288561