标签：return shu 报告 long find CF916E 解题 LCA gen

被这道题搞了一个晚上，还好搞出来了qwq

令人耳目一新的阅读体验

题目简述

翻译已经很简单了。

前置知识

DFS序，LCA，线段树，不需要标签中的树剖！

DFS序更新信息及判断祖先

如果你还不知道DFS序的话，我可以简单地讲一讲。

我们遍历一整棵树，设一个二维数组 h[i][0/1] 和tot，在第一次遍历到点 u 时 ++tot ，并使 \(h[u][0] = tot\) ，遍历完点 u 子树后再次 ++tot ，并使 \(h[u][1] = tot\) 。

这样子，如果 v 在 u 的子树内，则 \(h[u][0]<h[v][0]\) 并且 \(h[u][1]>h[v][1]\) 。原因可以通过 h 数组的定义得出。

据此，我们可以想象，在 h[u][0] 和 h[u][1] 之间的数都处于 u 的子树内。我们便可以根据 h 数组用线段树维护子树信息。但由于每个数都出现了两次，所以结果要除二。

题目解法

换根？他叫我换我就换，我是不是很没骨气？

其实我们可以发现，如果真的把根换了，题目中的 LCA ，子树，都要重新统计。所以我们选择不换根。

根据题意，我们令 gen 为现在题目中的根。实际上，我们不妨让根一直为 1 。

操作 1

将 gen 重新赋值就行

操作 3

令进行更改的节点为 u 。如果 u 不为 gen 的祖先，那么我们直接统计子树就好。

如果 u 为 gen的祖先，这样直接统计会有问题。

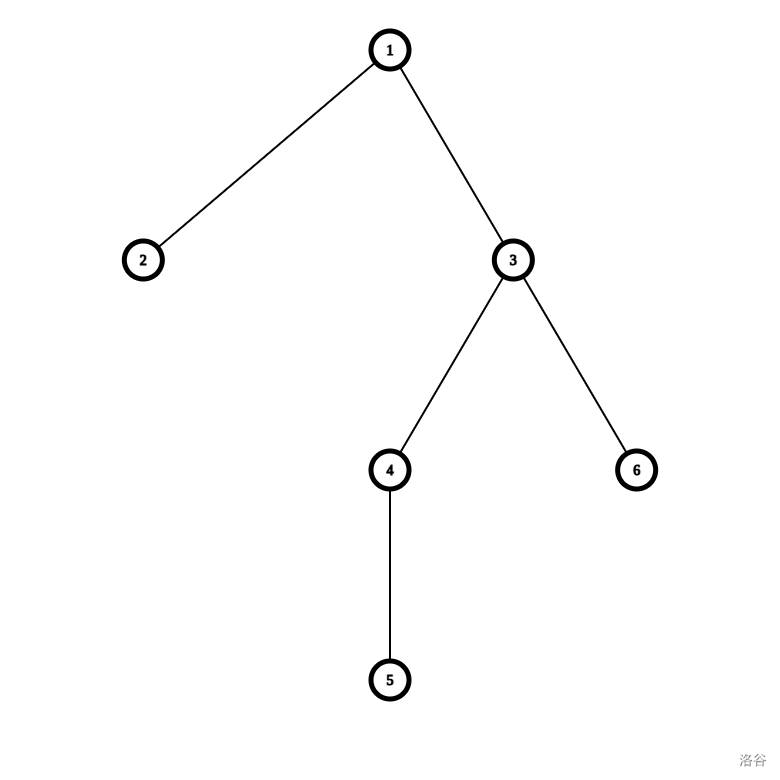
例如样例，假设现在 \(gen=3\) ， \(u=1\) ，1 更改时会把 3 和他的子树加到答案中。但这棵子树并不该被统计。

我们可以构造一组更极端的数据

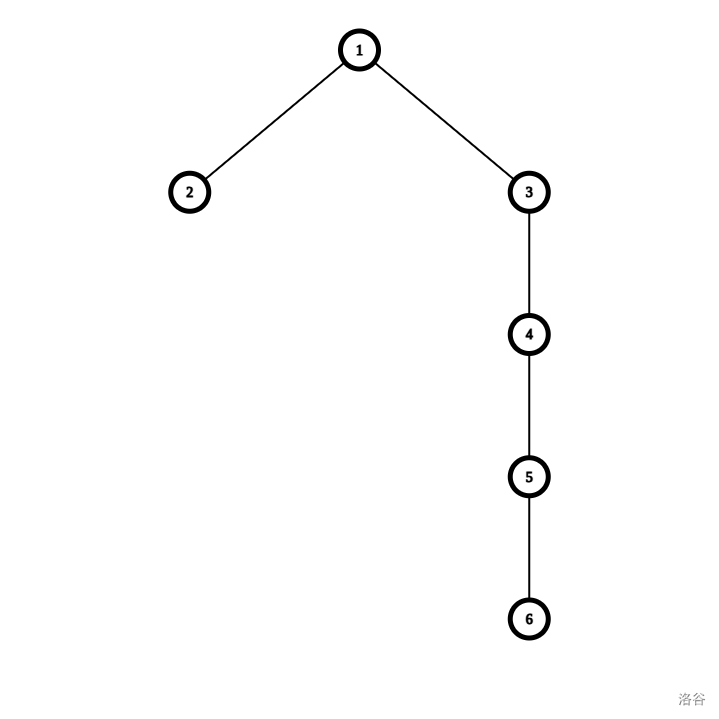
假设现在 \(gen=6\) ， \(u=1\) ，可以发现本来只有 1 和 2 会被更改。这是因为另一个子树由于根的变化，现在是它的祖先。

发现，如果 u 为 gen的祖先，有 gen 在的那颗子树就不能被统计，其他点都需要被统计。我们用 LCA 用剩下的倍增数组往上跳，跳到 u 的儿子。这棵子树不应该被更改。

具体地，我们统计整棵树的和，再减去这棵子树的和就好。

注意要特判 \(u=gen\) 的情况。此时统计全树之和。

操作 2

一看，有个LCA。这咋办？我们不妨再根据几个数据找规律。

在接下来的讨论中，设我们要求 u 和 v 的LCA。设 LCA(u,v) 为 l 。

我们发现，如果 l 不为根的祖先，那么啥事没有，我们返回 l 就好。

这是因为，如果不为祖先，说明 l 要么与 gen 在一个节点不同子树中，要么在 gen 的子树中，在这两种情况下， 1 为根还是 gen 为根没有区别。

如果 l 为根的祖先，那么这时，由于祖先情况发生了变化，有可能出现有一个节点为了与另一个节点相会，在 gen 到 1 这条链上走过。但这时我们的 LCA 显然要不会走这条链，所以为 LCA(gen,u) 或者 LCA(gen,v)。

到底是哪个呢？是以 1 为根，深度最深的那一个。显然，这个更靠近 gen 。

我们可以想象两个节点如何相会的：一个节点到他与 gen 的 LCA 停止，另一个节点到她与 gen 的LCA后转而向下走直到与第一个节点相会。

求出 LCA 后，就与操作 2 大同小异了。我们更改整棵树，然后再对那一棵子树（具体请参见操作 2 ）进行符号翻转的更改就好。

同样地，注意 \(LCA=gen\) 的情况。此时直接修改整棵树

code

#include <bits/stdc++.h> 
using namespace std;
const long long maxn = 2e5 + 5;
inline long long read(){
    char ch = getchar(); long long x = 0, f = 1;
    while(ch < '0' || ch > '9') 
	{
        if(ch == '-') f = -1;
        ch = getchar();
    } 
	while('0' <= ch && ch <= '9') 
	{
        x = x * 10 + ch - '0';
        ch = getchar();
    } 
	return x * f;
}
long long n, m;
long long a[maxn];
vector<long long> e[maxn];
void add(long long u, long long v){ e[u].push_back(v); }
long long d[maxn], f[maxn][23], h[maxn][2], tot;
void dfs(long long u, long long fa)
{
	h[u][0] = ++ tot;
	for(auto v : e[u])
	{
		if(v == fa) continue;
		d[v] = d[u] + 1;
		f[v][0] = u;
		dfs(v, u);
	}
	h[u][1] = ++ tot;
}
void init(){ for(long long j = 1;j <= 20;j ++) for(long long i = 1;i <= n;i ++) f[i][j] = f[f[i][j - 1]][j - 1]; }
long long LCA(long long u, long long v)
{
	if(d[u] < d[v]) swap(u, v);
	for(long long i = 20;i >= 0;i --) if(d[u] - (1 << i) >= d[v]) u = f[u][i];
	if(u == v) return u;
	for(long long i = 20;i >= 0;i --) if(f[u][i] != f[v][i]) u = f[u][i], v = f[v][i];
	return f[u][0];
}
struct linetree
{
	long long tr[maxn << 3], lt[maxn << 3];
	#define ls(u) (u<<1)
	#define rs(u) (u<<1)+1
	void push_up(long long u){ tr[u] = tr[ls(u)] + tr[rs(u)]; }
	void c(long long l, long long r, long long u, long long k){ tr[u] += (r - l + 1) * k, lt[u] += k; }
	void push_down(long long l, long long r, long long u)
	{
		long long mid = l + r >> 1;
		c(l, mid, ls(u), lt[u]);
		c(mid + 1, r, rs(u), lt[u]);
		lt[u] = 0;
	}
	void change(long long l, long long r, long long u, long long fl, long long fr, long long k)
	{
		if(l >= fl && r <= fr){ tr[u] += (r - l + 1) * k, lt[u] += k; return; }
		if(fl > r || fr < l) return ;
		push_down(l, r, u);
		long long mid = l + r >> 1;
		change(l, mid, ls(u), fl, fr, k);
		change(mid + 1, r, rs(u), fl, fr, k);
		push_up(u);
	}
	long long find(long long l, long long r, long long u, long long fl, long long fr)
	{
		if(l >= fl && r <= fr){ return tr[u]; }
		if(fl > r || fr < l) return 0;
		push_down(l, r, u);
		long long mid = l + r >> 1, ans = 0;
		ans += find(l, mid, ls(u), fl, fr);
		ans += find(mid + 1, r, rs(u), fl, fr);
		return ans;	
	}
}shu;
long long find(long long u, long long fin)//跳到 u 的儿子
{
	for(long long i = 20;i >= 0;i --) if(d[u] - (1 << i) > d[fin]) u = f[u][i];
	return u;
}
bool pdzu(long long u, long long v)//判断 u 是否为 v 的祖先
{
	return (h[u][0] < h[v][0]) && (h[u][1] > h[v][1]);
}
long long gen;
long long findlca(long long u, long long v)//找 LCA
{
	long long l = LCA(u, v);
	if(!pdzu(l, gen)){ return l; }
	long long a = LCA(gen, u), b = LCA(gen, v);
	return (d[a] > d[b]) ? a : b;
}
void tian(long long u, long long x)
{
	if(pdzu(u, gen))
	{
		long long v = find(gen, u);
		shu.change(1, 2 * n, 1, h[1][0], h[1][1], x); 
		shu.change(1, 2 * n, 1, h[v][0], h[v][1], -x); 
		return ;
	}
	else if(gen == u)
	{
		shu.change(1, 2 * n, 1, h[1][0], h[1][1], x);
		return ;
	}
	shu.change(1, 2 * n, 1, h[u][0], h[u][1], x);
}
long long cha(long long u)
{
	if(pdzu(u, gen))
	{
		long long ans = 0;
		long long v = find(gen, u);
		ans += shu.find(1, 2 * n, 1, h[1][0], h[1][1]);
		ans -= shu.find(1, 2 * n, 1, h[v][0], h[v][1]); 
		return ans;
	}
	else if(gen == u) {return shu.find(1, 2 * n, 1, h[1][0], h[1][1]);}
	return shu.find(1, 2 * n, 1, h[u][0], h[u][1]);
}
signed main()
{
	gen = 1;
	n = read(), m = read();
	for(long long i = 1;i <= n;i ++) a[i] = read(); 
	long long u, v, w, x;
	for(long long i = 1;i < n;i ++)
	{
		u = read(), v = read();
		add(u, v);add(v, u);
	}
	dfs(1, -1);init();
	for(long long i = 1;i <= n;i ++) 
	{
		shu.change(1, 2 * n, 1, h[i][0], h[i][1], a[i]);
		if(h[i][0] + 1 < h[i][1]) shu.change(1, 2 * n, 1, h[i][0] + 1, h[i][1] - 1, -a[i]);
	}
	for(long long _ = 1;_ <= m;_ ++)
	{
		w = read();u = read();
		if(w == 1) gen = u;
		if(w == 2)
		{
			v = read();x = read();
			long long l = findlca(u, v);	
			tian(l, x);
		}
		if(w == 3) printf("%lld\n", cha(u) / 2);
	}
	return 0;
}

总结

没有头绪时可以自己构造数据发现规律。

DFS序可以用于处理与子树有关的问题。

标签：return,shu,报告,long,find,CF916E,解题,LCA,gen
From： https://www.cnblogs.com/closureshop/p/16811499.html