P1971 [NOI2011] 兔兔与蛋蛋游戏 题解

Description

这些天，兔兔和蛋蛋喜欢上了一种新的棋类游戏。

这个游戏是在一个 \(n\) 行 \(m\) 列的棋盘上进行的。游戏开始之前，棋盘上有一个格子是空的，其它的格子中都放置了一枚棋子，棋子或者是黑色，或者是白色。

每一局游戏总是兔兔先操作，之后双方轮流操作，具体操作为：

• 兔兔每次操作时，选择一枚与空格相邻的白色棋子，将它移进空格。
• 蛋蛋每次操作时，选择一枚与空格相邻的黑色棋子，将它移进空格。

第一个不能按照规则操作的人输掉游戏。为了描述方便，下面将操作“将第 \(x\) 行第 \(y\) 列中的棋子移进空格中”记为 \(M(x,y)\)。

例如下面是三个游戏的例子。

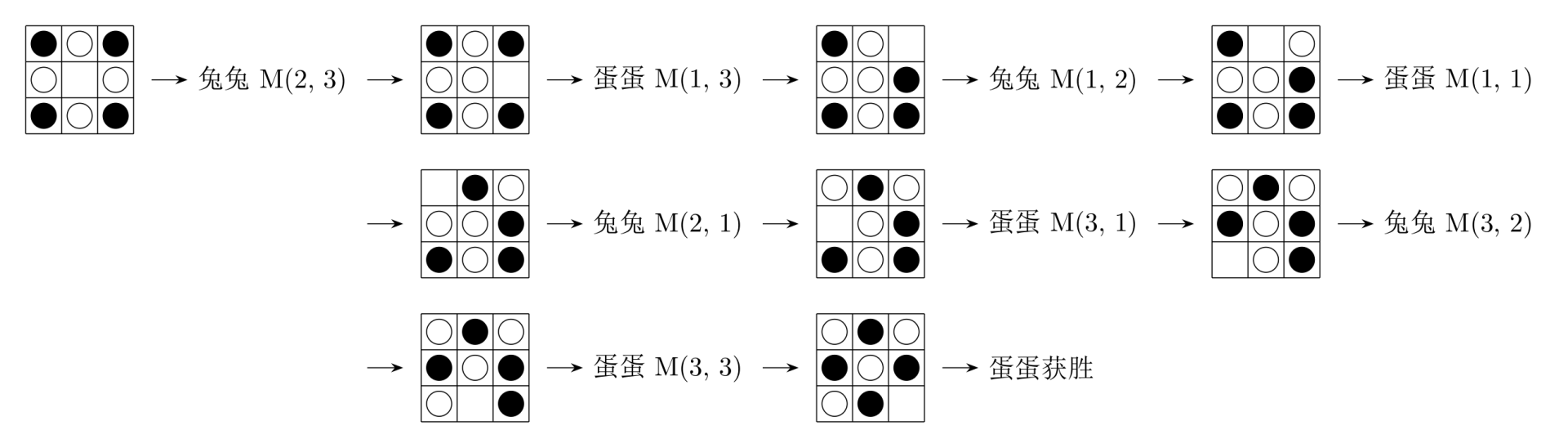
最近兔兔总是输掉游戏，而且蛋蛋格外嚣张，于是兔兔想请她的好朋友——你——来帮助她。她带来了一局输给蛋蛋的游戏的实录，请你指出这一局游戏中所有她“犯错误”的地方。

注意：

• 两个格子相邻当且仅当它们有一条公共边。
• 兔兔的操作是“犯错误”的，当且仅当，在这次操作前兔兔有必胜策略，而这次操作后蛋蛋有必胜策略。

\(1\leq n,m\leq 40\)。

Solution

考虑什么样的情况是必胜状态。

先有一个性质，就是一个位置最多被空格经过一次。

因为如果经过 \((x,y)\) 两次，则这两次之间的操作次数一定为偶数，那么如果最开始空格走到一个原本为黑色的格，那么 \((x,y)\) 就变成了黑色，而经过偶数次后再要回到 \((x,y)\) 必须要求 \((x,y)\) 为白色，矛盾。

所以一个位置最多被经过一次。

那么按照初始状态染色，黑格或者空格染黑，白格染白，那么每次一定是走到相邻的且未经过的颜色不同的格子。

按照这个颜色进行黑白染色就变成一个二分图的问题，即：有一个起点 \(s\)，每次走到有连边的未经过的点，走不了的输，问谁有必胜策略。

有个结论是先手必胜等价于起点是最大匹配的必经点。

证明就是如果起点是必经点，设走到 \(x\)，\(x\) 的下一步一定是个必经点，否则 \(x\) 连下一步的点一定构成一个新的最大匹配。所以先手每步都会走到必经点，所以其必定能走到它的匹配点。而后手到最后总会先走不动，所以先手必胜。

如果起点是非必经点，则下一步一定走到必经点，否则也能构造出一个更大的匹配。然后就变成了起点是必经点的问题，所以这里先手必败。

所以题目就变成了每次删点，然后判断一个点是否为最大匹配必经点。考虑倒着做，每次加点然后在残量网络上跑网络流，如果有更新则为必经点。

然后这题就做完了。

时间复杂度：\(O(knm\sqrt{nm})\)。

Code

#include <bits/stdc++.h>

// #define int int64_t

const int kMaxN = 2e3 + 5, kMaxM = 1e5 + 5;
const int kD[][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

int n, m, k;
int col[45][45], x[kMaxN], y[kMaxN], cnt[kMaxN];
bool del[kMaxN];

int getid(int x, int y) { return (x - 1) * m + y; }

namespace Dinic {
struct Node {
  int v, w, pre;

  Node(int _v = 0, int _w = 0, int _pre = 0) : v(_v), w(_w), pre(_pre) {}
} e[kMaxM];

int n, s, t, tot = 1, tail[kMaxN], cur[kMaxN], dep[kMaxN];
bool vis[kMaxN];

void addedge(int u, int v, int w) { e[++tot] = {v, w, tail[u]}, tail[u] = tot; }
void add(int u, int v, int w) { addedge(u, v, w), addedge(v, u, 0); }
void init(int _n, int _s, int _t) {
  n = _n, s = _s, t = _t, tot = 1, std::fill_n(tail, n + 1, 0);
}

bool bfs() {
  for (int i = 1; i <= n; ++i)
    cur[i] = tail[i], vis[i] = 0, dep[i] = 1e9;
  std::queue<int> q;
  q.emplace(s), dep[s] = 0, vis[s] = 1;
  for (; !q.empty();) {
    int u = q.front(); q.pop();
    for (int i = tail[u]; i; i = e[i].pre) {
      int v = e[i].v, w = e[i].w;
      if (w && !vis[v]) {
        dep[v] = dep[u] + 1, vis[v] = 1, q.emplace(v);
      }
    }
  }
  return vis[t];
}

int dfs(int u, int lim) {
  if (u == t || !lim) return lim;
  int flow = 0;
  for (int &i = cur[u]; i; i = e[i].pre) {
    int v = e[i].v, w = e[i].w;
    if (w && dep[v] == dep[u] + 1) {
      int fl = dfs(v, std::min(lim, w));
      if (!fl) dep[v] = 1e9;
      e[i].w -= fl, e[i ^ 1].w += fl;
      lim -= fl, flow += fl;
      if (!lim) break;
    }
  }
  return flow;
}

int maxflow() {
  int ans = 0;
  for (; bfs(); ans += dfs(s, 1e9)) {}
  return ans;
}
}  // namespace Dinic

void dickdreamer() {
  std::cin >> n >> m;
  int s = n * m + 1, t = n * m + 2;
  Dinic::init(n * m + 2, s, t);
  // 0 : 白，1 : 黑
  for (int i = 1; i <= n; ++i) {
    std::string str;
    std::cin >> str;
    str = " " + str;
    for (int j = 1; j <= m; ++j) {
      if (str[j] == '.') x[0] = i, y[0] = j, del[getid(i, j)] = 1;
      if (str[j] == 'O') col[i][j] = 0;
      else col[i][j] = 1;
      if (!col[i][j]) Dinic::add(s, getid(i, j), 1);
      else Dinic::add(getid(i, j), t, 1);
    }
  }
  std::cin >> k;
  for (int i = 1; i <= 2 * k; ++i) {
    std::cin >> x[i] >> y[i];
    del[getid(x[i], y[i])] = 1;
  }
  for (int i = 1; i <= n; ++i) {
    for (int j = 1; j <= m; ++j) {
      if (col[i][j] || del[getid(i, j)]) continue;
      for (auto [di, dj] : kD) {
        int ti = i + di, tj = j + dj;
        if (col[ti][tj] && !del[getid(ti, tj)])
          Dinic::add(getid(i, j), getid(ti, tj), 1);
      }
    }
  }
  cnt[2 * k + 1] = Dinic::maxflow();
  for (int i = 2 * k; ~i; --i) {
    int u = getid(x[i], y[i]);
    del[u] = 0;
    for (auto [di, dj] : kD) {
      int tx = x[i] + di, ty = y[i] + dj, v = getid(tx, ty);
      if (tx < 1 || tx > n || ty < 1 || ty > m) continue;
      if (col[tx][ty] != col[x[i]][y[i]] && !del[v]) {
        if (!col[x[i]][y[i]]) Dinic::add(u, v, 1);
        else Dinic::add(v, u, 1);
      }
    }
    cnt[i] = Dinic::maxflow();
  }
  std::vector<int> vec;
  for (int i = 1; i <= k; ++i) {
    if (cnt[2 * i - 2] && cnt[2 * i - 1])
      vec.emplace_back(i);
  }
  std::cout << vec.size() << '\n';
  for (auto x : vec) std::cout << x << '\n';
}

int32_t main() {
#ifdef ORZXKR
  freopen("in.txt", "r", stdin);
  freopen("out.txt", "w", stdout);
#endif
  std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);
  int T = 1;
  // std::cin >> T;
  while (T--) dickdreamer();
  // std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";
  return 0;
}