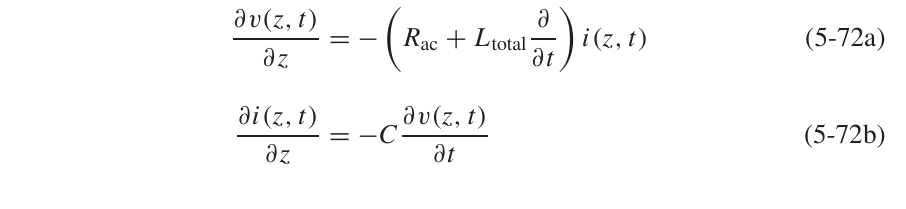Nonideal Conductor Models
1. 在非闭合导体中传播的信号
1.1 传播常数
从Maxwell‘s Equations可以导出如下旋度方程:
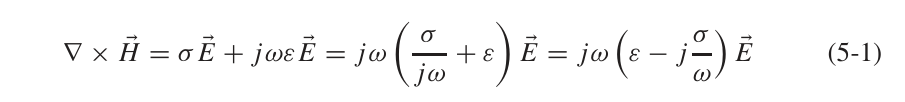
更进一步的,可以将介电常数展开成频变的
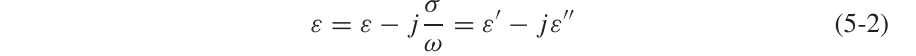
这里方程等号右边的项整体会被视作$\gamma^{2}$,由于该项前面的$j\omega$,括号内的虚部最终会导致信号的衰减,实部会导致相位常数的变化。
对于一个金属导体来说,介质损耗是不存在的,因此可以得到传播常数:
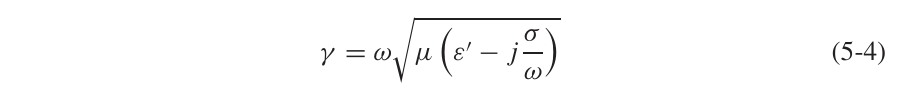
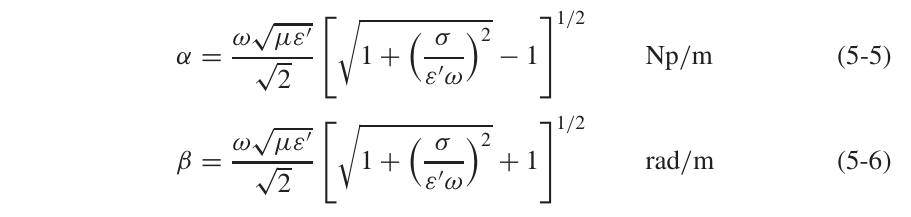
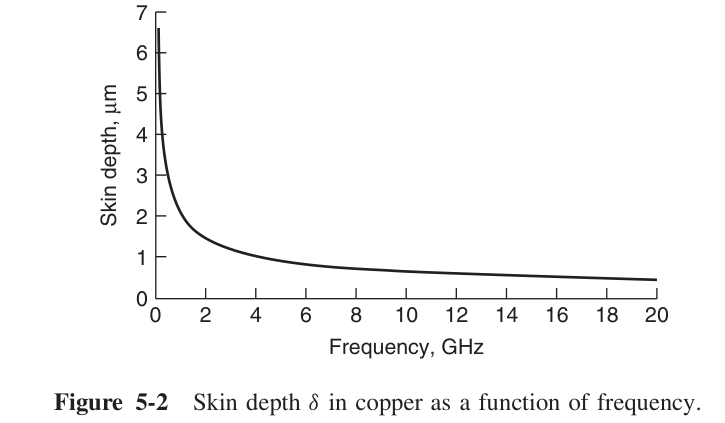
1.2 趋肤深度
将频域下在金属导体中传播的波函数转换成时域形式,可以得到:
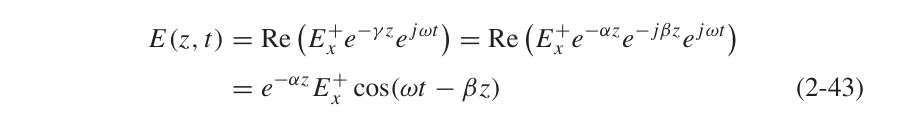
趋肤深度的定义就是当电磁波的赋值衰减为$e^{-1}$时对应的深度,对于良导体来说,有
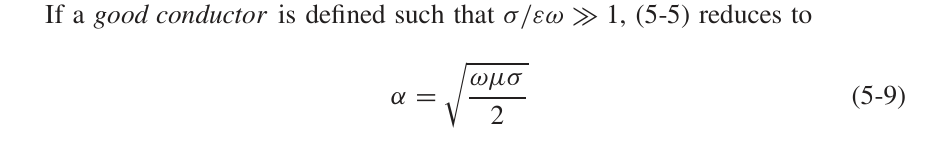
从而可以推导出趋肤深度为:
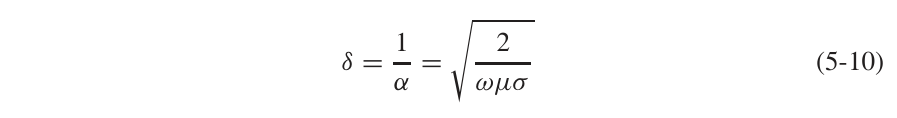
2. 传输线的经典导体模型
2.1 直流损耗 (DC Resistance)
经典的电阻公式:
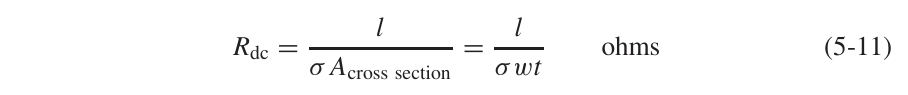
2.2 频变损耗 (AC Resistance)
2.2.1对于微带线来说
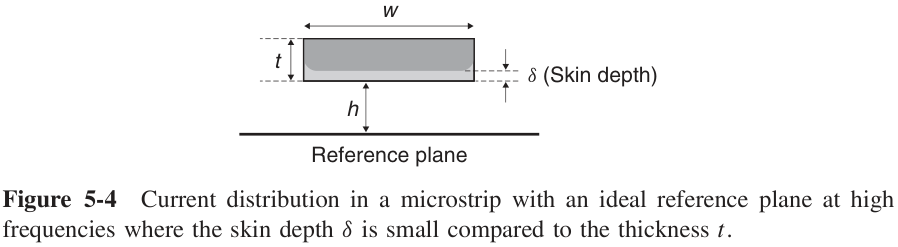
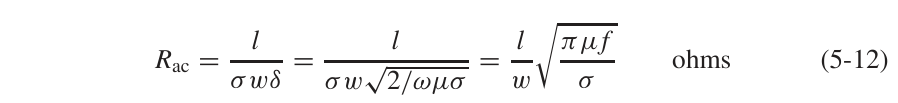
- 对于趋肤深度近似的讨论
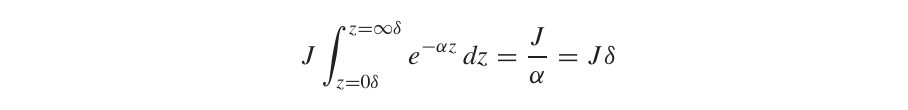
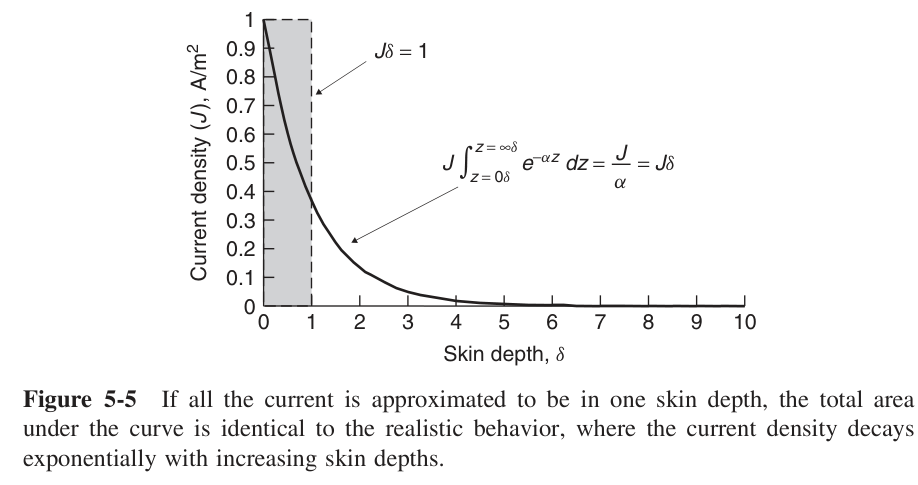
- 电阻曲线
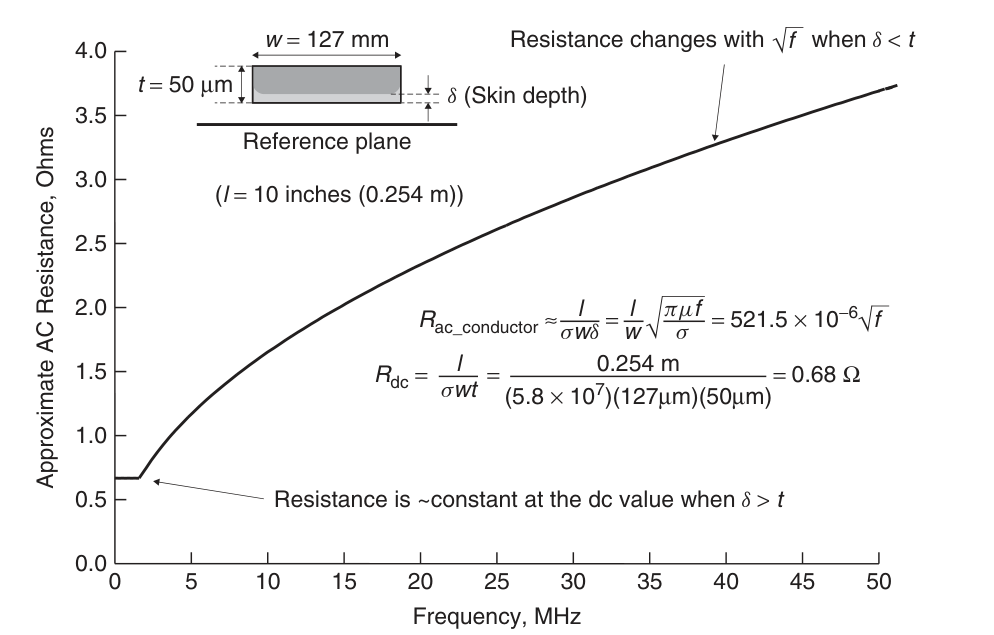
可以看到电阻曲线先不变,然后会产生一个跳变。但在现实中,这种跳变是不存在的,采用平方开根号的方法来平滑曲线:
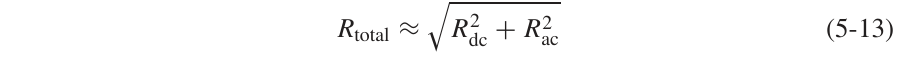
除了信号线之外,地的电阻也应当被考虑。
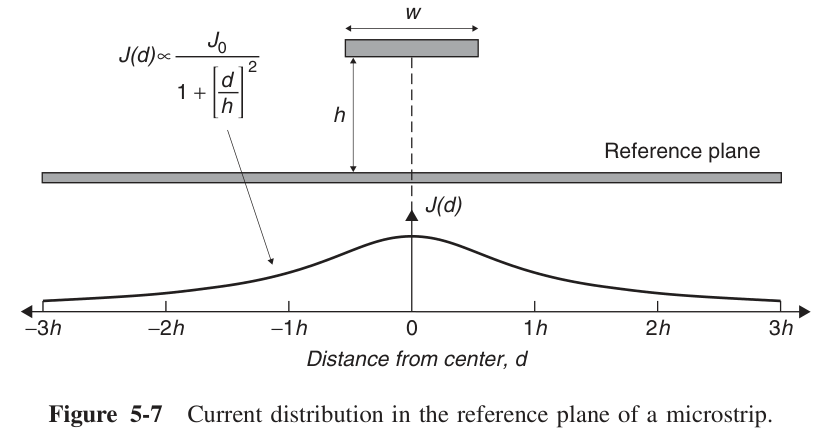
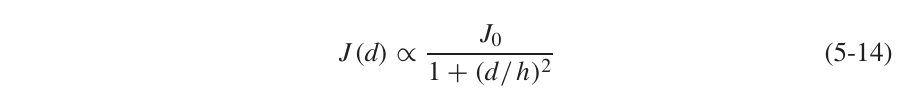
地上的电流密度满足上述关系,可以看到h越小d的系数就越大,电流密度随着位置远离中心点变化也越剧烈,说明电流越集中。通常选取w=6h去计算地上的电阻:
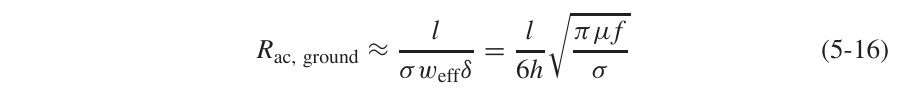
所以微带线的完整的交流电阻应为:
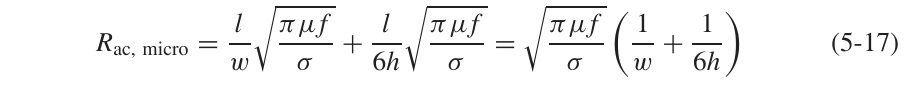
2.2.2 Stripline
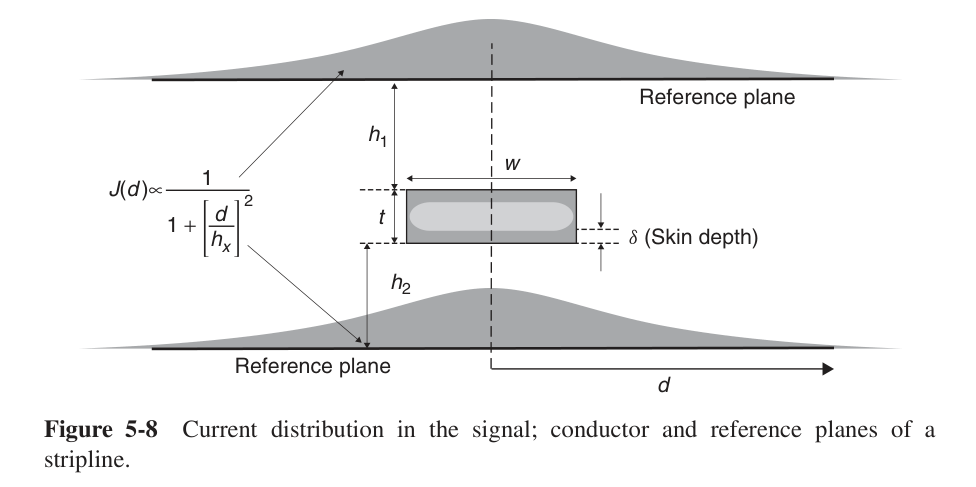
将Stripline看成是两个微带线并联,其电阻就可使用电路的知识得到:
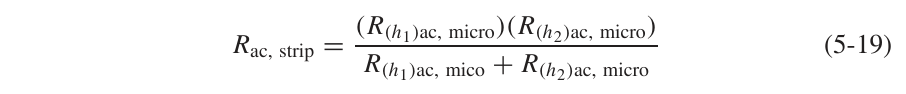
2.3 频变电感
趋肤效应的另一个结果:导致频变的电感值。
在低频时,电流分布在整个导体内,高频时电流由于趋肤深度被挤到导体表面。
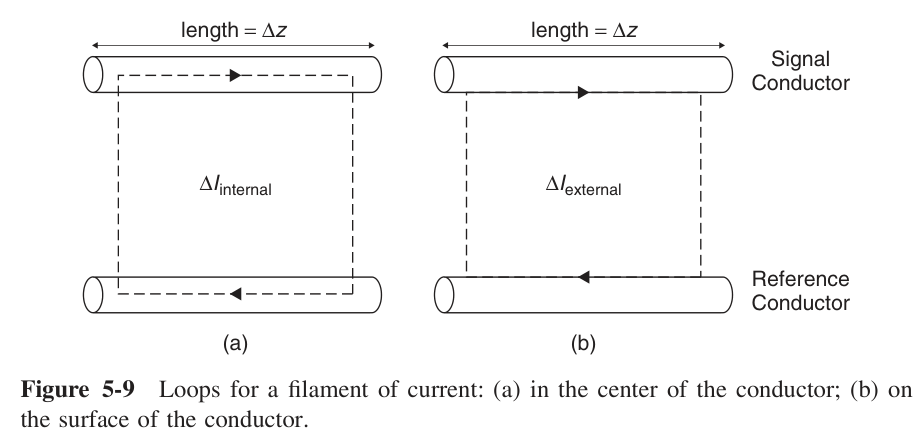
根据电感的定义:
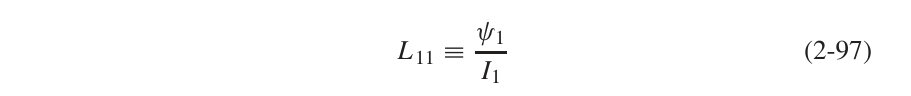
随着loop的减小,电感值会受到影响。
完整的电感值可以被分为两个方面,其数学表达式为:
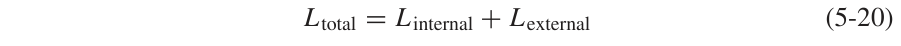
对于良导体来说,位移电流可以忽略不计,因此,磁场的旋度定理可以被简化为:
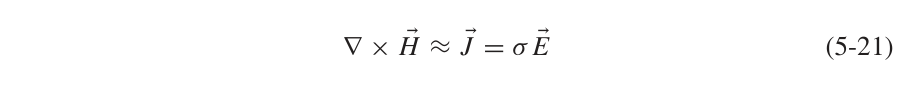
结合电场的旋度定理,利用双叉乘恒等式可得二阶偏微分方程:
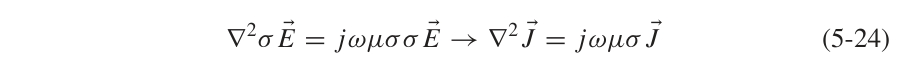
设定J沿着z方向,偏微分只对x作偏导,可以得到:
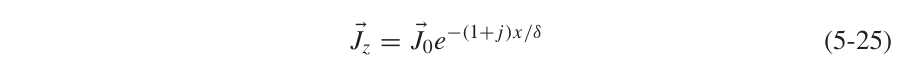
完整的电流可以使用积分积出来:
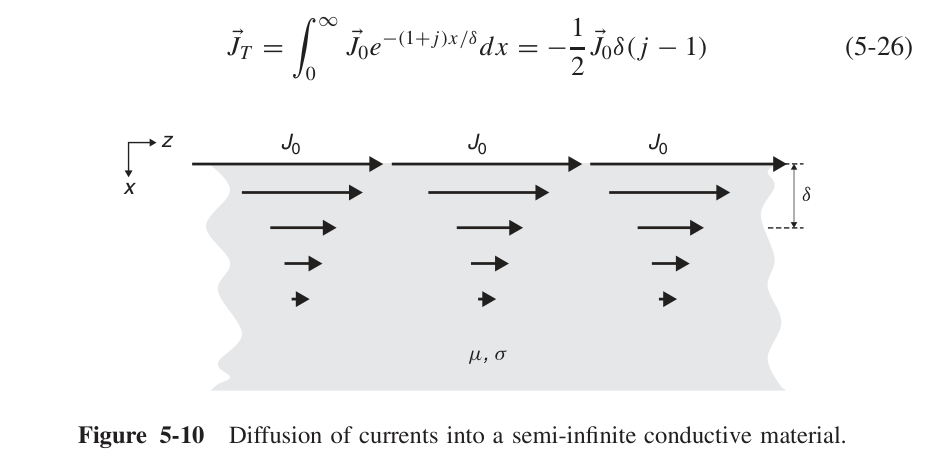
从而可以引出一个表面阻抗的概念:
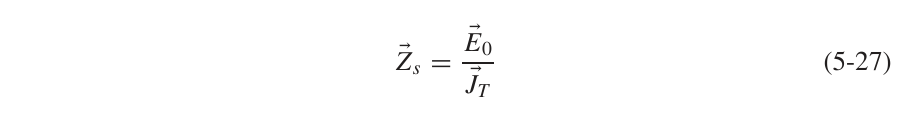
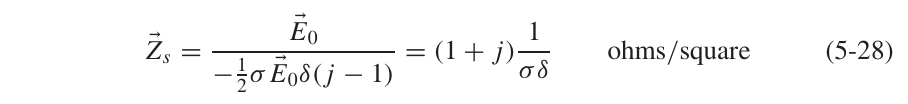
从(5-28)这个式子中我们可以看到,表面阻抗的实部和虚部是一样的,其可以有另一种表达形式:
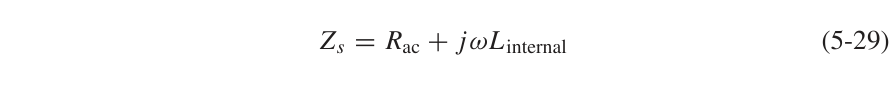
令(5-28)和(5-29)相等,可以得到:
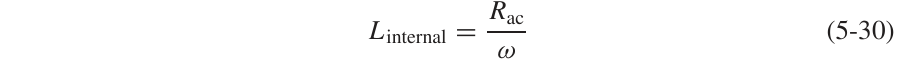
至于Lexternal,利用传输线的特征阻抗和相速度可以求得:
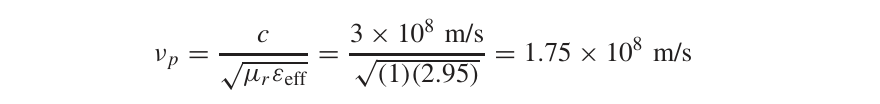
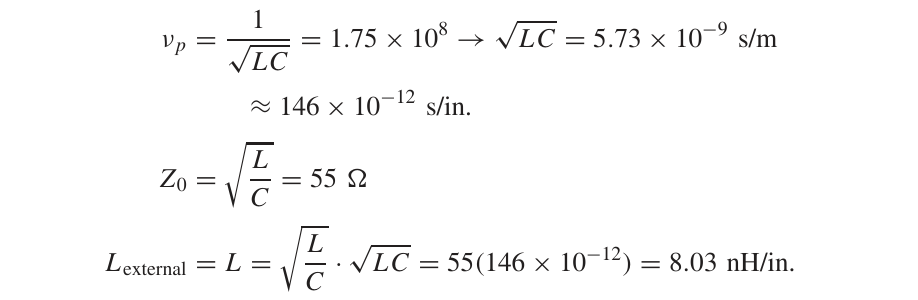
2.4 良导体表面吸收的功率
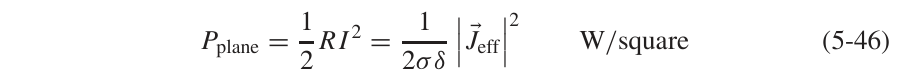
3. 粗糙度对损耗的影响
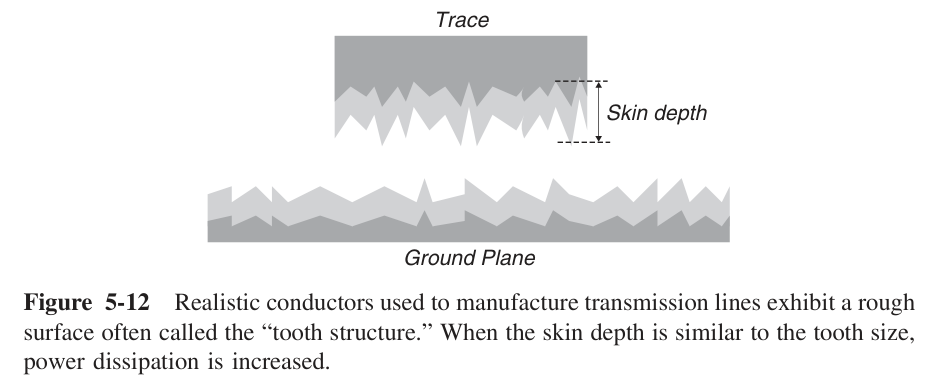
当趋肤深度和粗糙度的齿深接近时,对损耗的影响比较大。从电阻的角度来说等效的电流路径变长了,从而导致电阻变大,损耗变大。
总之总的趋势就是损耗会变大,粗糙度越高,损耗相比于光滑金属导体就越大。
4. 非理想导体传输线的一些参数
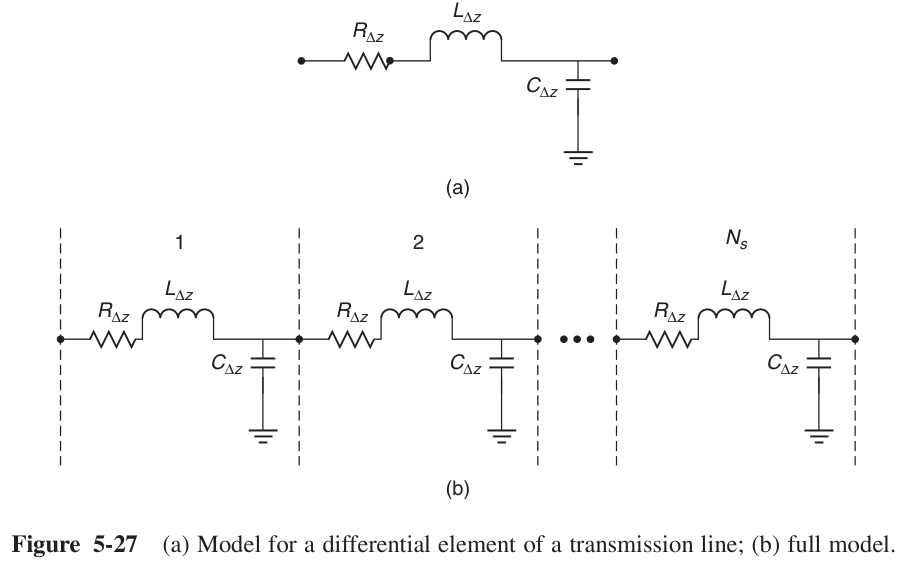
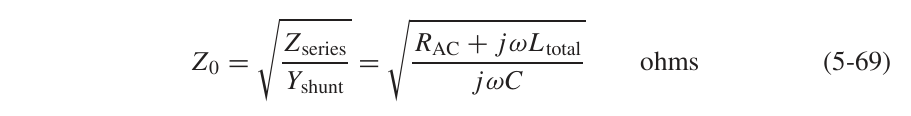
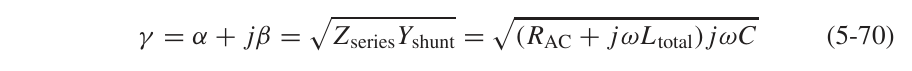
- 对应的电报方程: