首页 > 其他分享 >无限之环 题解

无限之环 题解

时间：2024-06-08 09:22:41浏览次数：25  
标签：右点 int 题解 之环 lst flw 无限 水管 dis

五星压行大师 \(lyh\) 表示：这是难得能让他的代码长度打破百行大关的题目（182行）。

首先，根据科技与狠活，本题可以黑白染色。源点联向白格，黑格连向汇点。

发现每个格子都可以连向四个方向，所以可以建立四个点，代表水管连到了上下左右四个方向。

设四元组 \((x,y,z,p)\) 表示水管初始状态下，是否联向上、右、下、左。若 \(x==1\)，则从源点联向上点（黑格则从上点联向汇点），以此类推。

例如：格子是白格，代表的水管初始状态接口在上和右，我们就从源点联向格子上点和右点；格子是黑格，就从上点和右点联向汇点。

当然，相邻格子间的上下左右是相通的，要从白格的上下左右点联向上方格子的下点、下方格子的上点、左方格子的右点、右方格子的左点。

我们用样例 1 做例子：

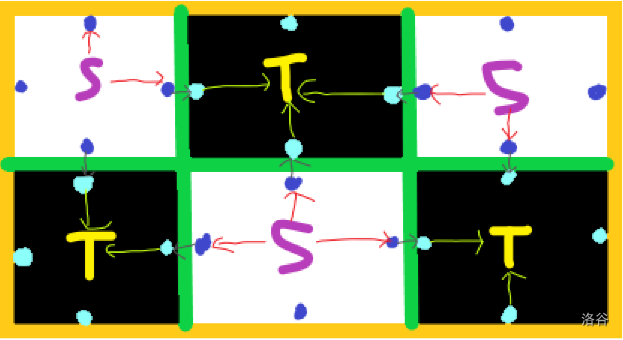
由于这些边都是生来就有的，所以不用支付任何费用，流量都为 1，记为 \((1,0)\)。

由于水管可以旋转，所以我们肯定还需要再连一些边。

当然，直水管不能旋转，十字型水管转了没用，所以不用考虑。

由于黑格只需要和白格反着来就可以，所以只讨论白格：

  1. Q形管（只伸出一根水管）
    我们以 \((1,0,0,0)\) 这样的水管为例。
    发现旋转一次可以到达左点或右点，两次可以到达下点。
    那么从上点向左、右点连 \((1,1)\)，向下点连 \((1,2)\)。

  2. T形管（伸出三根水管）
    我们以 \((1,1,1,0)\) 这样的水管为例。
    发现旋转一次上、下点为 0，两次右点为 0，而旋转后左点都为 1。
    因而可以看作上、下、右点变成了左点。
    根据 Q形管 思路，上点、下点、右点向左点连 \((1,1),(1,1),(1,2)\)。

  3. L形管（伸出相邻两根水管）
    我们以 \((1,1,0,0)\) 这样的水管为例。
    根据上述思路，可以很快想到上点向下点连 \((1,1)\)，右点向左点连 \((1,1)\)。
    旋转两次相当于同时经过上面两条边，所以不连。

我们将完整版的图再画一下（新增蓝、粉边都是 \((1,1)\)，其余为 \((1,2)\)）：

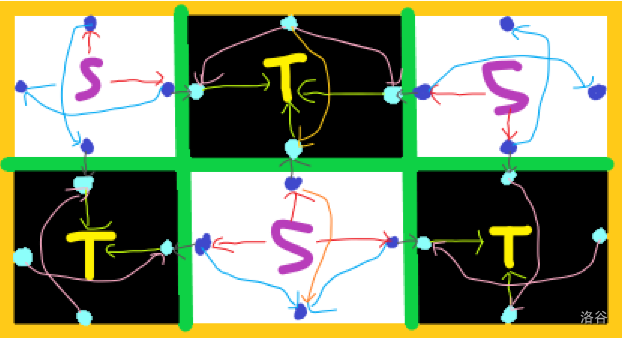
假如不漏水，一定会经过 \(sm=\sum(x+y+z+p)\) 条边。

发现每一条增广路经过且只经过 2 条水管，所以当最大流 \(<sm\) 时，输出 -1。

其他情况下，答案即为最小费用。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=14005,M=30005;
int n,m,s,t,k=1,h[N],vis[N];
int to[M],nxt[M],w[M],f[M];
int lst[N],flw[N],dis[N],sm;
int sh(int u,int v){
	return 4*(u*m-m+v-1)+1;
}int xi(int u,int v){
	return 4*(u*m-m+v-1)+2;
}int zu(int u,int v){
	return 4*(u*m-m+v-1)+3;
}int yo(int u,int v){
	return 4*(u*m-m+v-1)+4;
}void add(int x,int y,int z,int a){
    w[++k]=z;f[k]=a;to[k]=y;
    nxt[k]=h[x];h[x]=k;
    f[++k]=-a;to[k]=x;
    nxt[k]=h[y];h[y]=k;
}queue<int>q;
int spfa(){
    while(q.size()) q.pop();
    memset(lst,-1,sizeof(lst));
    memset(vis,0,sizeof(vis));
    memset(dis,127,sizeof(dis));
    flw[s]=1e9;dis[s]=0;q.push(s);
    while(q.size()){
        int x=q.front();
        q.pop();vis[x]=0;
        for(int i=h[x];i;i=nxt[i]){
            int y=to[i],vl=w[i];
            if(vl&&dis[y]>dis[x]+f[i]){
                lst[y]=i;
                flw[y]=min(flw[x],vl);
                dis[y]=dis[x]+f[i];
                if(!vis[y])
                    q.push(y),vis[y]=1;
            }
        }
    }return lst[t]!=-1;
}int mxflw,mncst;
void MCMF(){
    while(spfa()){
        mxflw+=flw[t];
        mncst+=dis[t]*flw[t];
        for(int i=t;i!=s;i=to[lst[i]^1])
            w[lst[i]]-=flw[t],w[lst[i]^1]+=flw[t];
    }if(mxflw*2!=sm) cout<<-1;
	else cout<<mncst; 
}void white(int l,int u,int v){
	if(u>1) add(sh(u,v),xi(u-1,v),1,0);
	if(u<n) add(xi(u,v),sh(u+1,v),1,0);
	if(v>1) add(zu(u,v),yo(u,v-1),1,0);
	if(v<m) add(yo(u,v),zu(u,v+1),1,0);
	if(!l) return;
	int x=0,y=0,z=0,p=0;
	if(l&1) x=1;if(l&2) y=1;
	if(l&4) z=1;if(l&8) p=1;
	sm+=x+y+z+p;
	if(x) add(s,sh(u,v),1,0);
	if(z) add(s,xi(u,v),1,0);
	if(p) add(s,zu(u,v),1,0);
	if(y) add(s,yo(u,v),1,0);
	if(x&&!y&&z&&!p) return;
	if(!x&&y&&!z&&p) return;
	if(x&&y&&z&&p) return;
	if(x&&!y&&!z&&!p){
		add(sh(u,v),xi(u,v),1,2);
		add(sh(u,v),zu(u,v),1,1);
		add(sh(u,v),yo(u,v),1,1);
	}if(!x&&y&&!z&&!p){
		add(yo(u,v),sh(u,v),1,1);
		add(yo(u,v),zu(u,v),1,2);
		add(yo(u,v),xi(u,v),1,1);
	}if(!x&&!y&&z&&!p){
		add(xi(u,v),sh(u,v),1,2);
		add(xi(u,v),zu(u,v),1,1);
		add(xi(u,v),yo(u,v),1,1);
	}if(!x&&!y&&!z&&p){
		add(zu(u,v),sh(u,v),1,1);
		add(zu(u,v),yo(u,v),1,2);
		add(zu(u,v),xi(u,v),1,1);
	}if(x&&y&&z&&!p){
		add(sh(u,v),zu(u,v),1,1);
		add(yo(u,v),zu(u,v),1,2);
		add(xi(u,v),zu(u,v),1,1);
	}if(x&&y&&!z&&p){
		add(sh(u,v),xi(u,v),1,2);
		add(yo(u,v),xi(u,v),1,1);
		add(zu(u,v),xi(u,v),1,1);
	}if(x&&!y&&z&&p){
		add(sh(u,v),yo(u,v),1,1);
		add(zu(u,v),yo(u,v),1,2);
		add(xi(u,v),yo(u,v),1,1);
	}if(!x&&y&&z&&p){
		add(xi(u,v),sh(u,v),1,2);
		add(yo(u,v),sh(u,v),1,1);
		add(zu(u,v),sh(u,v),1,1);
	}if(!x&&!y&&z&&p){
		add(xi(u,v),sh(u,v),1,1);
		add(zu(u,v),yo(u,v),1,1);
	}if(x&&y&&!z&&!p){
		add(sh(u,v),xi(u,v),1,1);
		add(yo(u,v),zu(u,v),1,1);
	}if(x&&!y&&!z&&p){
		add(sh(u,v),xi(u,v),1,1);
		add(zu(u,v),yo(u,v),1,1);
	}if(!x&&y&&z&&!p){
		add(xi(u,v),sh(u,v),1,1);
		add(yo(u,v),zu(u,v),1,1);
	}
}void black(int l,int u,int v){
	if(!l) return;
	int x=0,y=0,z=0,p=0;
	if(l&1) x=1;if(l&2) y=1;
	if(l&4) z=1;if(l&8) p=1;
	sm+=x+y+z+p;
	if(x) add(sh(u,v),t,1,0);
	if(z) add(xi(u,v),t,1,0);
	if(p) add(zu(u,v),t,1,0);
	if(y) add(yo(u,v),t,1,0);
	if(x&&!y&&z&&!p) return;
	if(!x&&y&&!z&&p) return;
	if(x&&y&&z&&p) return;
	if(x&&!y&&!z&&!p){
		add(xi(u,v),sh(u,v),1,2);
		add(zu(u,v),sh(u,v),1,1);
		add(yo(u,v),sh(u,v),1,1);
	}if(!x&&y&&!z&&!p){
		add(sh(u,v),yo(u,v),1,1);
		add(zu(u,v),yo(u,v),1,2);
		add(xi(u,v),yo(u,v),1,1);
	}if(!x&&!y&&z&&!p){
		add(sh(u,v),xi(u,v),1,2);
		add(zu(u,v),xi(u,v),1,1);
		add(yo(u,v),xi(u,v),1,1);
	}if(!x&&!y&&!z&&p){
		add(sh(u,v),zu(u,v),1,1);
		add(yo(u,v),zu(u,v),1,2);
		add(xi(u,v),zu(u,v),1,1);
	}if(x&&y&&z&&!p){
		add(zu(u,v),sh(u,v),1,1);
		add(zu(u,v),yo(u,v),1,2);
		add(zu(u,v),xi(u,v),1,1);
	}if(x&&y&&!z&&p){
		add(xi(u,v),sh(u,v),1,2);
		add(xi(u,v),yo(u,v),1,1);
		add(xi(u,v),zu(u,v),1,1);
	}if(x&&!y&&z&&p){
		add(yo(u,v),sh(u,v),1,1);
		add(yo(u,v),zu(u,v),1,2);
		add(yo(u,v),xi(u,v),1,1);
	}if(!x&&y&&z&&p){
		add(sh(u,v),xi(u,v),1,2);
		add(sh(u,v),yo(u,v),1,1);
		add(sh(u,v),zu(u,v),1,1);
	}if(!x&&!y&&z&&p){
		add(sh(u,v),xi(u,v),1,1);
		add(yo(u,v),zu(u,v),1,1);
	}if(x&&y&&!z&&!p){
		add(xi(u,v),sh(u,v),1,1);
		add(zu(u,v),yo(u,v),1,1);
	}if(x&&!y&&!z&&p){
		add(xi(u,v),sh(u,v),1,1);
		add(yo(u,v),zu(u,v),1,1);
	}if(!x&&y&&z&&!p){
		add(sh(u,v),xi(u,v),1,1);
		add(zu(u,v),yo(u,v),1,1);
	}
}signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin>>n>>m;t=n*m*4+1;
    for(int i=1;i<=n;i++)
    	for(int j=1;j<=m;j++){
    		int x;cin>>x;
    		if((i+j)&1) black(x,i,j);
    		else white(x,i,j);
		}
	MCMF();return 0;
}//spfa:它没有死透

标签：右点,int,题解,之环,lst,flw,无限,水管,dis
From： https://www.cnblogs.com/chang-an-22-lyh/p/18238249/wuxianzhihuan_tj

相关文章

  • 开车旅行|倍增优化dp+双端列表/set|题解
    题面:题面链接这题的思路值得借鉴,也是我做的第一道倍增优化dp题目.比较好的是题目的意思较为清晰,所以不再赘述.解析:这里我们可以非常直接的想到暴力模拟,因为第一眼看上去前七个点的数据范围是支持我们进行一个简单的预处理得到对应人在对应位置的决策的.(排序O(n×sqrt(......
  • [ABC107D] Median of Medians 题解
    题目大意：一个长度为$M$的序列的中位数为这个序列从小到大排序后第$\lfloor\fracM2\rfloor+1$个数，将这个序列的所有子段的中位数放入一个序列中，求这个序列的中位数。设一个序列$a$的中位数为$x$，那么$a$中至少会有一半的数大于等于$x$，并且$x$是$a$中满足这个条件......
  • プログラミングコンテストチャレンジブック 题解
    题目大意：从$n$根木棒里选出六根拼成两个合法的三角形，使这两个三角形的周长和最大。考虑贪心，证明在后面。首先我们要知道一个三角形基本定理：较短两边长度之和大于最长边。那我们就根据这个定理先去寻找最大三角形的最长边。先排序，然后循环枚举，对于每个$a_i$，可以寻找到的最大......
  • [COCI2020-2021#2] Sjekira 题解
    题目大意：把一棵树完全分解，每次分解一条边的代价是这条边连接的两个连通块的最大点权之和，求最小代价。逆序模拟，既然题目要求将树完全分解，那我们就每次逆序连接当前权值最小的两个点，也就是贪心的思路。尝试将贪心的值写成一个表达式：$$\sum_{i=1}^na_i+\sum_{(u,v)\inE}\max(a......
  • [ABC036D] 塗り絵 题解
    题意题面讲挺清楚的就不简化了。思路树上求方案数，很明显是树上dp。设$dp_{i,0/1}$表示第$i$个点涂成白/黑色的方案数。当前结点如果为白色，那么它的子节点涂成什么颜色都没关系，根据分步乘法原理，将它子结点涂成白/黑色的方案数之和乘起来即可；当前结点如果为黑色，那么它的子......
  • [ABC126D] Even Relation 题解
    题意对一棵有$N$个点，$N-1$条边的树进行黑白染色，使得每两个距离为偶数的点颜色都一致。思路首先让我们回顾一下加法的性质：偶$+$偶$=$偶奇$+$奇$=$偶偶$+$奇$=$奇不难看出，距离为偶数的关系是可以传递的，而距离为奇数的关系不行。我们只需要做一遍dfs，对一个......
  • [ABC191E] Come Back Quickly 题解
    题面：给你一个$n$个点$m$条边的有向图，第$i$条边$a_i$，$b_i$，$c_i$，表示一条单向边从$a_i$到$b_i$，长度为$c_i$，可能会有重边和自环。问能否从第$i$号点出发然后回到该点形成一个环？可以则输出最短时间，否则输出$-1$。思路：不难发现本题考查的是最短路。观察题面，发现边数......
  • [ABC126F] XOR Matching 题解
    很好的构造题。题意请构造一个长度为$2^{m+1}$的序列$a$，该序列满足：$\foralli\in[1,2^{m+1}],a_i\in[0,2^m-1]$且每个数都恰好出现两次。对于任意一对$(i,j)$满足$a_i=a_j$，$a_i\oplusa_{i+1}\oplus\cdots\oplusa_{j-1}\oplusa_j=k$。$\oplus$表......
  • 食物链题解
    由题得，所有动物整体关系如上。起初每个动物相互时间没有关系，bb[i]=i。对于x与y：如果它们是同类即x到y的距离为$0$，或者转了几圈，一圈距离为$3$，即模$3$余$0$。如果x捕食y，就是x到y距离模$3$余$1$。对x与y操作时：如果它们没有关系(它们不被之前给出的某......
  • 题解：ABC270G Sequence in mod P
    题目传送门思路题目给出了一个数列\[x_{i+1}\equiv{a\timesx_i+b}\pmod{p}\]并想要求最小的\(x_i=G\)，那我们可以考虑求出这个数列的通项公式。具体的，观察到原式可以转化成一个等比数列的形式，所以我们可以先设一个常数\(k\)，使得\[x_{i+1}+k=a(x_i+k)\]替换进原先的式子......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99