比较直接的做法。
当 \(P_x = 1\) 时显然可以暴力 DP,设 \(f_{x,c}\) 表示 \(x\) 的子树中以 \(c\) 开头的最长不下降子序列的长度。直接转移即可。
\(P_x \neq 1\) 的时候呢?我们发现,所谓“忽略掉这些路径中的第 \(2\) 到第 \(P_x\) 个的点”,代表的就是按照深度转移,大概就是这样:
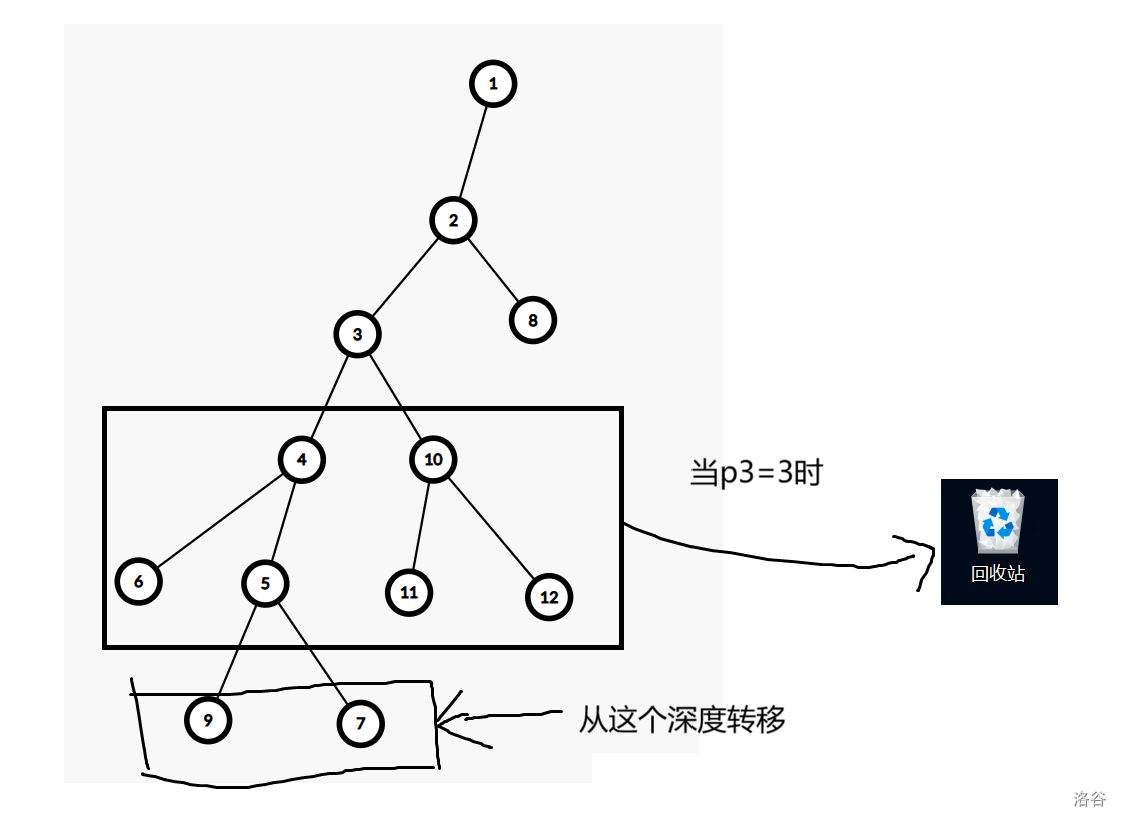
只和深度有关,很难不想到长链剖分,套板子即可。
转移方程(其中 \(mxdep\) 代表其最大深度)
\[ans = \begin{cases} 1 \quad P_x \ge mxdep_x\\ max_{f_{dfn_x+P_x,c}} \quad c<c_x\\max_{f_{dfn_x+P_x,c}}+1 \quad c \ge c_x\end{cases} \]一定要在回溯时就统计答案,要不然答案就会被祖先覆盖然后就会和我一样寄掉。
时间复杂度 \(O(n\left|\Sigma\right|)\)。
代码
#include<bits/stdc++.h>
using namespace std;
inline void rd(){}
template<typename T,typename ...U>
inline void rd(T &x,U &...args){
char ch=getchar();
T f=1;x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x*=f;rd(args...);
}
const int N=1e5+5;
char ch[N];
int n,p[N],fst[N],nxt[N<<1],v[N<<1],idx;
void Add(int a,int b){
v[idx]=b,nxt[idx]=fst[a];
fst[a]=idx++;
}
int mxdep[N],son[N],dfn[N],cnt;
int ans[N];
void DFS(int x,int f){
mxdep[x]=1;
for(int i=fst[x];~i;i=nxt[i]){
int y=v[i];
if(y==f)continue;
DFS(y,x);
mxdep[x]=max(mxdep[x],mxdep[y]+1);
if(mxdep[y]>mxdep[son[x]])son[x]=y;
}
}
void DFS2(int x,int f){
dfn[x]=++cnt;
if(son[x])DFS2(son[x],x);
for(int i=fst[x];~i;i=nxt[i]){
int y=v[i];
if(y==f||y==son[x])continue;
DFS2(y,x);
}
}
int f[N][30],c[N];
void Solve(int x,int fa){
if(son[x])Solve(son[x],x);
for(int i=fst[x];~i;i=nxt[i]){
int y=v[i];
if(y==fa||y==son[x])continue;
Solve(y,x);
for(int j=1;j<=mxdep[y];j++){
for(int k=1;k<=26;k++){
f[dfn[x]+j][k]=max(f[dfn[x]+j][k],f[dfn[y]+j-1][k]);
}
}
}
if(son[x])for(int i=1;i<=26;i++)f[dfn[x]][i]=max(f[dfn[x]][i],f[dfn[x]+1][i]);
for(int i=c[x];i<=26;i++)f[dfn[x]][c[x]]=max(f[dfn[x]][c[x]],f[dfn[x]][i]+1);
int pls=0;
if(p[x]==1){
for(int j=1;j<=26;j++){
ans[x]=max(ans[x],f[dfn[x]][j]);
}
}else{
if(p[x]>=mxdep[x])ans[x]=1;
else{
for(int j=1;j<=26;j++){
if(j>=c[x])pls=1;
ans[x]=max(ans[x],f[dfn[x]+p[x]][j]+pls);
}
}
}
}
signed main(){
memset(fst,-1,sizeof fst);
rd(n);
for(int i=1;i<=n;i++)rd(p[i]);
scanf("%s",ch+1);
for(int i=1;i<=n;i++)c[i]=ch[i]-'a'+1;
for(int i=1;i<n;i++){
int x,y;rd(x,y);
Add(x,y);Add(y,x);
}
DFS(1,1);DFS2(1,1);
Solve(1,1);
for(int i=1;i<=n;i++)printf("%d\n",ans[i]);
return 0;
}