Another Filling the Grid
题目信息
题目描述
You have $ n \times n $ square grid and an integer $ k $ . Put an integer in each cell while satisfying the conditions below.
- All numbers in the grid should be between $ 1 $ and $ k $ inclusive.
- Minimum number of the $ i $ -th row is $ 1 $ ( $ 1 \le i \le n $ ).
- Minimum number of the $ j $ -th column is $ 1 $ ( $ 1 \le j \le n $ ).
Find the number of ways to put integers in the grid. Since the answer can be very large, find the answer modulo $ (10^{9} + 7) $ .
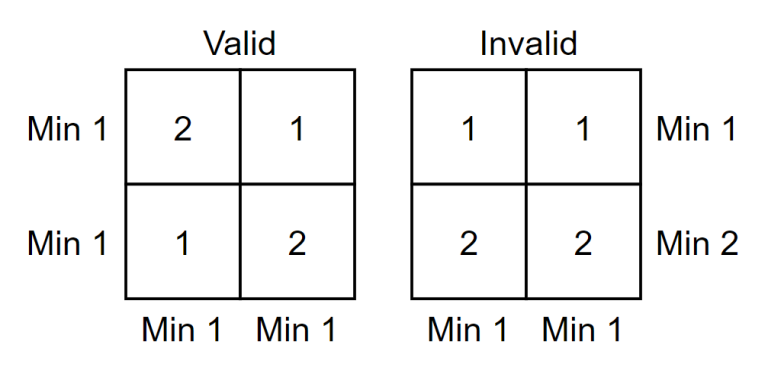These are the examples of valid and invalid grid when $ n=k=2 $ .
输入格式
The only line contains two integers $ n $ and $ k $ ( $ 1 \le n \le 250 $ , $ 1 \le k \le 10^{9} $ ).
输出格式
Print the answer modulo $ (10^{9} + 7) $ .
样例 #1
样例输入 #1
2 2
样例输出 #1
7
样例 #2
样例输入 #2
123 456789
样例输出 #2
689974806
提示
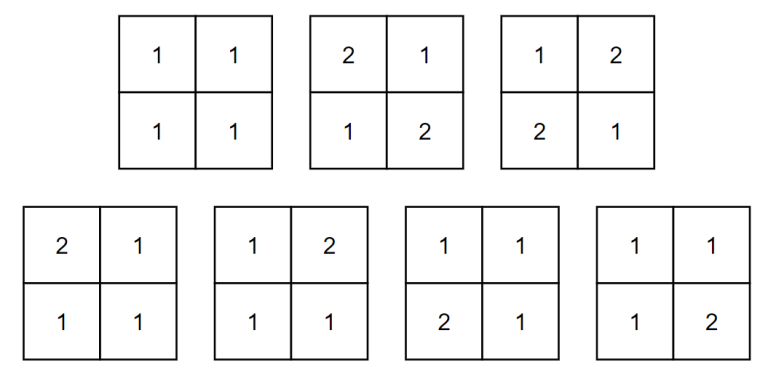
In the first example, following $ 7 $ cases are possible.
In the second example, make sure you print the answer modulo $ (10^{9} + 7) $ .
题面翻译
给定一个 \(n\times n\) 的矩阵，用 \(1\sim k\) 的数填充，每行每列最小值均为 \(1\)，问有多少填法，对 \(10^9+7\) 取模。
\(1\le n\le 250,1\le k\le 10^9\)。