时间: 24_05_30
原题:Codeforces Round 947 (Div. 1 + Div. 2)
标签: 二分/数据结构/[[DFS]]/[[模拟]]/[[树形结构]]
题目大意
有 \(n\) 个顶点的树,初始时每个节点都是白色
树上有两个棋子,为\(P_A\) 和 \(P_B\) ,分别位于 \(a\) , \(b\) 顶点
\(P_A\) 所在的顶点会被涂成红色,\(P_B\) 经过的顶点如果是红色,那么该顶点变成蓝色
每次两棋子各走一步,问最少几次所有顶点会变成蓝色
思路
分解问题
- 首先解决一个问题,假定 \(P_A\) 和 \(P_B\) 在同一个顶点上,那么最短的路径是多少?
我们可以画个图,要想经过所有顶点,每条路径都要经过两次,除了拘留 \(P_A\) 最远的点
换句话说,以 \(a\) 为根节点,节点数为 \(n\) ,树的最大深度为 \(mx\) ,则此时的最优解为 \(2*(n-1)-mx\)
- 第二个问题,现在a与b不是同一位置,此时我们需要一个不太严谨的猜想:pa与pb先在ab点碰面,再从ab点出发,此时为最优解
简单的解释一下,思考\(P_A\) 和 \(P_B\) 在整个过程中的运动,最后的答案关键在于 \(P_B\) 点的结束次数
那么不考虑路径重复等复杂问题,先让两点移动到5,再从5开始dfs,可以得到最优答案
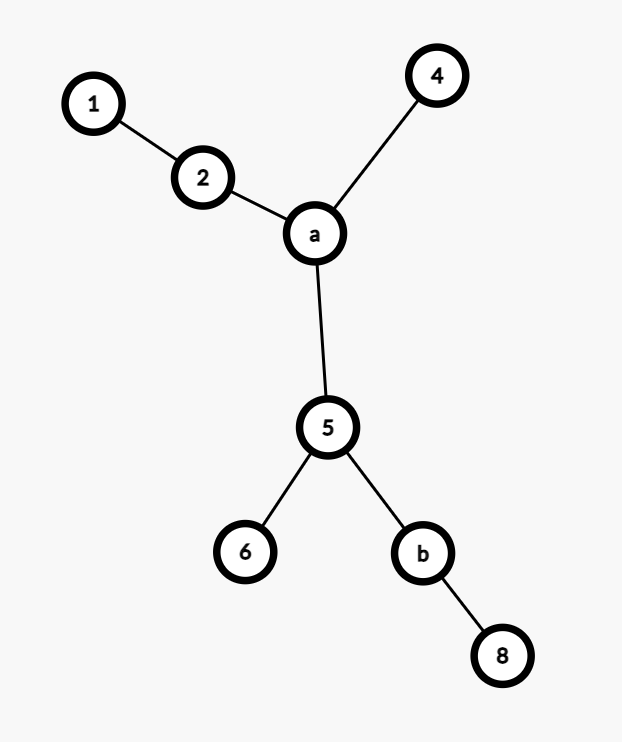
解决流程
-
以a为根结点dfs造树
-
找出最合适的点ab
-
以ab为根结点造树
-
根据ab找出的mx和从a到ab的cnt找出答案
代码
#include<iostream>
#include<vector>
#include<functional>
using namespace std;
#define int long long
#define endl "\n"
const int N = 2e5 + 10;
int _, n, u, v, a, b;
vector<int>g[N];
vector<int>f(N);//father
vector<int>dep(N);
void solve() {
cin >> n;
for (int i = 0; i <= n; i++) {
g[i].clear();
dep[i] = 0;
f[i] = 0;
}
cin >> a >> b;
for (int i = 0; i < n - 1; i++) {
cin >> u >> v;
g[u].emplace_back(v);
g[v].emplace_back(u);
}
//1. 以a为根结点dfs造树
function<void(int, int)>dfs = [&](int r, int fa) {
//先建树
f[r] = fa;
//再取dep
dep[r] = dep[fa] + 1;
//子树
for (auto i : g[r])
if (i != f[r])
dfs(i, r);
};
dfs(a, 0);
//2. 找出最合适的点ab
int ab = b;
int cnt = 0;
// 根据深度寻找最适合的ab
while (dep[ab] > (dep[a] + dep[b]) / 2) {
ab = f[ab];
cnt++;//同时记录cnt,即a和b走了多少次到达的ab
}
//3. 以ab为根结点造树
dfs(ab, 0);
//4. 根据ab找出的mx和从a到ab的cnt找出答案
int ans = 1e18;
for (int i = 1; i <= n; i++) //也可以在dfs中找mx,这里选择遍历一下找出最大深度
ans = min(ans, 2 * (n - 1) - (dep[i]-1) + cnt);//由于代码中根结点的深度为1,需要减去这个1
cout << ans << endl;
}
signed main() {
cin >> _;
while (_--)
solve();
return 0;
}