首页 > 其他分享 >第二章 线性表（4）

第二章 线性表（4）

时间：2024-05-24 19:59:58浏览次数：17  
标签：结点 线性表 head fast next 链表 第二章 cur

2.7.2 链表逆置问题（反转链表问题）

该部分参考了408之2023年算法题预测和力扣相关题解

解决这类问题，有三种方法，递归法、迭代法和头插法。头插法是教科书中创建链表的头插法在反转链表中的应用，但是需要依赖反转的第一个结点的前驱结点，如果该结点没有前驱结点，需要先创建一个dummy结点指向第一个结点，像是leetcode的风格中一般链表都没有头结点，但是408考试中链表都是带头结点的，因此这种方法必须掌握。而递归法和迭代法，均不需要dummy结点就可以进行反转链表，但是由于递归法的空间复杂度为 O ( n ) O(n) O(n) ，而迭代法的空间复杂度为 O ( 1 ) O(1) O(1) ，所以迭代法是反转链表的最优解法，大概率也是标准答案的解法，因此反转链表只需要掌握迭代法即可。

  1. 带有头结点的链表逆序(从尾到头)输出每个结点的值

    • 法一：先反转链表再遍历打印结点；反转链表方法见下面的具体例题；

    • 法二：递归法，空间复杂度为 O ( n ) O(n) O(n)

      //这是不带头结点的写法
void printList(LNode *L) {
    if(L -> next == NULL) {
        cout << L -> data << " ";     //递归出口
    }
    printList(L -> next);   
}

//带头结点的写法
void print(LNode *L) {
    if(L -> next == NULL) {
        cout << L -> data << " ";     //递归出口
    }
    print(L -> next);   
}

void printList(LNode *head) {
    print(head -> next);
}

    • 法三：将链表中的结点值依次入栈，再出栈输出即可

      void printList(LNode *L) {   //带头结点的情况
    stack<int> stk;
    stk.clear();   //先将栈清空，以免有脏数据；
    LNode *p = L -> next;    //若为不带头结点的链表这一步可省略；
    while(p != NULL) {
        stk.push(p -> data);
        p = p -> next;
    }
    while(!stk.empty()){
        int x = stk.pop();
        cout << x << " ";
    }    
}

  1. 反转链表

    不懂的可以看一下灵佬的视频讲解，十分透彻：反转链表【基础算法精讲 06】

    也可以看一下代码随想录这一节的讲解：https://programmercarl.com/0206.%E7%BF%BB%E8%BD%AC%E9%93%BE%E8%A1%A8.html#%E6%80%9D%E8%B7%AF

  • 【示例】：image-20230725132926756

  • 法一：头插法，该方法依赖于链表中第一个结点的直接前驱结点，如果是不带头结点的链表，可以设置一个dummy结点指向它；

    如图：image-20230725151856140

    //带头结点写法
LNode *reverseList(LNode *&L) {
    LNode *p = L -> next, *r;
    L -> next = NULL;   //将头结点和原来的链表断连；
    while(p) {
        r = p -> next;    //保存一下后继结点为后面更新p结点做准备；
        p -> next = L -> next;
        L -> next = p;     //采用头插法将遍历到的结点依次插入L头结点新组成的链表中；
        p = r;      //更新p指针继续向后遍历；
    }
    return L;
}

//无头结点写法
LNode* reverseList(LNode* &head){
    LNode*dummy =(LNode*) malloc(sizeof(LNode));
    dummy->data = 0,dummy->next = NULL;
    LNode* p =head,*r;
    while(p){
        r = p->next;
        p->next=dummy->next;
        dummy->next=p;
        p=r;

    }
    LNode*ans=dummy->next;
    return ans;																		
}

    时间复杂度： O ( n ) O(n) O(n),其中 n n n是链表的长度,需要遍历链表一次。

    空间复杂度： O ( 1 ) O(1) O(1)

  • 法二：迭代法：（⭐️⭐️⭐️⭐️重要模板，需记住！！！不懂的看灵神视频即可）

    解题思路：从前往后不断将未反转的结点加入到反转的链表中，可以将链表一分为二，左边是已反转的链表结点，右边是未反转的链表结点。初始时，已反转的链表部分为空，未反转的链表部分为整条链表。

    结束时，已反转的链表部分为整条链表，未反转的链表部分为空。

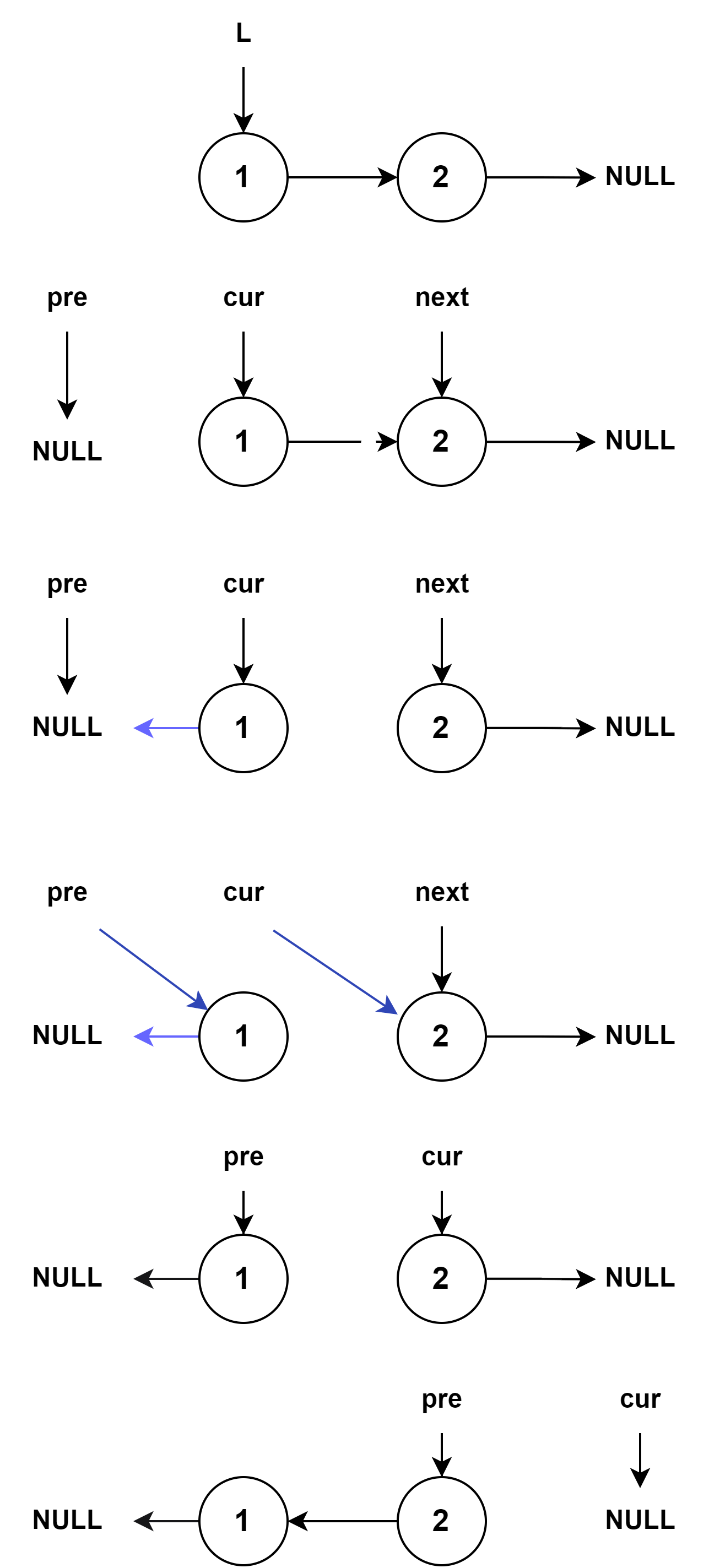
    image-20230725154311214img

    //不带头结点写法：这一部分可以就是反转链表的经典模板，必须掌握！！！输入待反转链表的第一个结点，可以返回反转后的链表
LNode* reverseList(LNode *&L) {
    LNode* pre = NULL, * cur = L;
    while(cur) {     //只要cur不为空，就意味着还有结点没有反转；
        LNode * next = cur -> next;   //因为后面cur要重连，但是下一步要改变cur -> next, 所以得先保存一下它的直接后继结点；
        cur -> next = pre;   //逆置的关键,反转操作
        //更新两个指针；
        pre = cur;     
        cur = next;   
    }
    return pre;     //迭代结束后链表逆置成功，此时pre为新链表的第一个结点，cur指向空结点；
}  

//带头结点写法，408风格
//调用前面的模板即可；
LNode *reverseList(LNode *&L) {
    L -> next = reverseListHelper(L -> next);
    return L;
}

    【注意】：⭐️⭐️⭐️反转结束后，从原链表上看，pre指向反转这一段的最后一个结点，cur指向反转这一段后续的下一个结点，这个性质很重要，后面的问题经常需要用到！！！

    时间复杂度： O ( n ) O(n) O(n),其中 n n n是链表的长度,需要遍历链表一次。

    空间复杂度： O ( 1 ) O(1) O(1)

  • 其他方法：递归法由于需要递归调用的栈空间，最多为 n n n层，因此空间复杂度为 O ( n ) O(n) O(n),而且处理不当可能会产生环从而陷入死循环；此外还可以用入栈出栈来实现逆置操作，但是不如上面的原地操作方法好，这里也不再介绍；

    //递归法：不带头结点写法。
ListNode* reverseList(ListNode* head) {
        if(head == NULL || head -> next == NULL){
            return head;  //递归出口；
        }
        ListNode* newnode = reverseList(head -> next);
        //假设当前结点的后面部分都已经反转，现在要让当前结点的后面一个结点的后续指向当前结点，而当前结点应该指向NULL；
        head -> next -> next = head;
        head -> next = NULL;
        return newnode;
}

  1. 反转链表进阶版,即反转部分链表

    给你带表头结点单链表的头指针head和两个整数left和right，其中 left小于或等于right。请你反转从链表中从第left个结点到第right个结点的链表段。

    例如将链表 $head→1→2→3→4→5 $中间的第2-4个结点反转为 h e a d → 1 → 4 → 3 → 2 → 5 head→1→4→3→2→5 head→1→4→3→2→5 。看上面链接的灵佬视频；

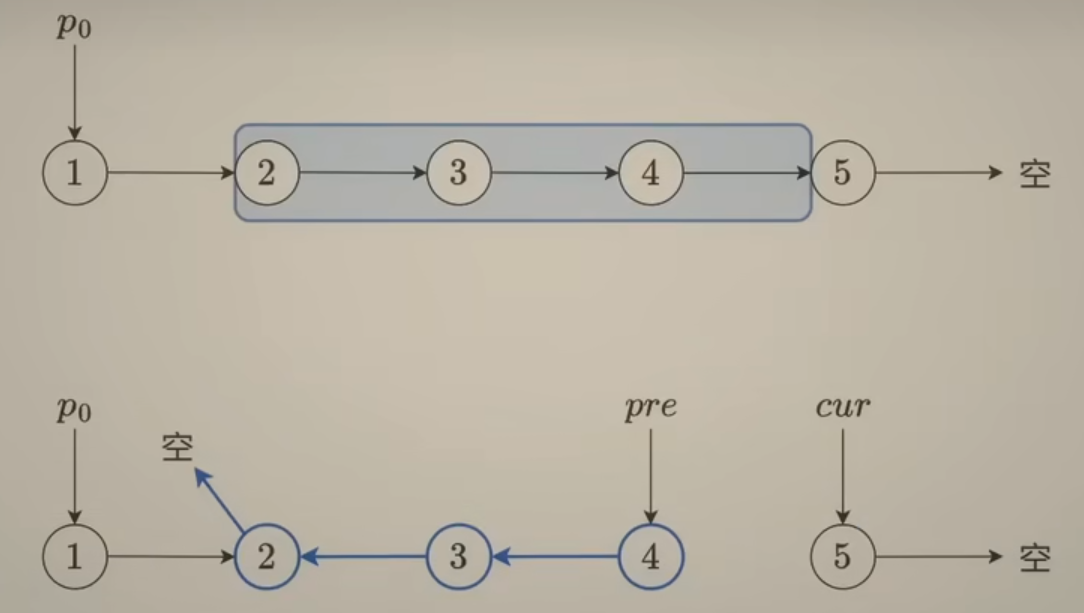
image-20230725161737022image-20230725161802965

图示是不带头结点的做法，但是如果left等于1时，P0不好处理，因此可以设置一个dummy哨兵结点指向第一个结点，那样的话当left等于1时，P0结点就是dummy结点；

不过408考试中都是带头结点的链表，也就没有这个烦恼了；这里应用到了反转链表的重要性质：反转结束后，从原链表上看，pre指向反转这一段的最后一个结点，cur指向反转这一段后续的下一个结点。

//带头结点的链表
LNode* reverseList(LNode *&head, int left, int right) {
    LNode *p0 = head;
    for(int i = 0; i < left - 1; ++i) {
        p0 = p0 ->  next;       //先找到链表中待反转部分的前一个结点，将其标记为p0;
    }
    //接下来就像之前反转链表那样操作即可，只不过由于只是反转部分链表，因此更换判断条件即可；
    LNode *pre = NULL, *cur = p0 -> next;
    for(int i = 0; i < right - left  +1; ++i) {
        LNode *next = cur -> next;
        cur -> next = pre;
        pre = cur;
        cur = next;
    }
    //中间部分反转完毕，接下来将其与原链表段的左右两部分连接即可；下面就是用到之前提到的那个性质的时候；
    p0 -> next -> next = cur;  //中间部分反转完毕后cur指向中间部分的后一个结点；
    p0 -> next = pre;    //反转完毕后从原链表视角看，pre指向待反转链表段的最后一个结点；结合上图一起看；
    //注意上面两步顺序一定不能调换！
    return head;
}

时空复杂度和之前的一样.

  1. K 个一组翻转链表

  • 题目描述:给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

    k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

    你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

  • 示例:img

    输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

  • image-20230725175929108image-20230725175849643

  • 解题代码:

    class Solution {
public:
    ListNode *reverseKGroup(ListNode *head, int k) {
        int n = 0;
        for (ListNode *cur = head; cur; cur = cur->next)
            ++n; // 统计节点个数

        ListNode *dummy = new ListNode(0, head), *p0 = dummy;
        ListNode *pre = nullptr, *cur = head;
        for (; n >= k; n -= k) {
            for (int i = 0; i < k; ++i) { // 下面的就是和之前一样的迭代法反转链表模板
                ListNode *nxt = cur->next;
                cur->next = pre; // 每次循环只修改一个 next，方便大家理解
                pre = cur;
                cur = nxt;
            }
            ListNode *nxt = p0->next;     //保存一下p0->next;
            p0->next->next = cur;
            p0->next = pre;
            p0 = nxt;     //始终让p0保持在待反转链表段的前一个结点处;
        }
        return dummy->next;
    }
};
    • 时间复杂度： O ( n ) O(n) O(n)，其中 n n n为链表节点个数。
    • 空间复杂度： O ( 1 ) O(1) O(1)，仅用到若干额外变量。
2.7.3 快慢指针问题

无法高效获取长度，无法根据偏移快速访问元素，是链表的两个劣势。然而我们经常碰见诸如获取倒数第k个元素，获取中间位置的元素，判断链表是否存在环，判断环的长度等和长度与位置有关的问题。这些问题都可以通过灵活运用双指针来解决。

请见灵神该视频:环形链表II【基础算法精讲 07】

代码随想录：142.环形链表II

  1. 链表的中间结点

  • 题目描述:给你单链表的头结点 head ，请你找出并返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。

  • 示例:

    • 例题1:img

      输入：head = [1,2,3,4,5]
输出：[3,4,5]
解释：链表只有一个中间结点，值为 3 。

    • 例题2:img

      输入：head = [1,2,3,4,5,6]
输出：[4,5,6]
解释：该链表有两个中间结点，值分别为 3 和 4 ，返回第二个结点。

  • 解题方法:快慢指针,定义一个快指针fast每次执行走两步,定义一个慢指针slow每次走一步,当fast下一步为空或已经为空时,此时slow所指结点就是要找的中间结点.

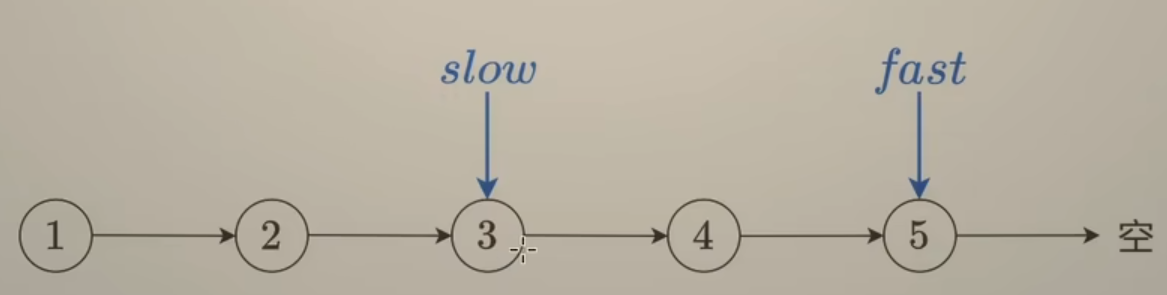
  • 如图两种情况image-20230725204448385image-20230725204540473

  • 代码:(⭐️重要模板)

    //不带头结点的情况
LNode* middleNode(LNode *head) {
    LNode *fast = head, *slow = head;
    while(fast && fast -> next) {
        fast = fast -> next -> next;
        slow = slow -> next;
    }
    return slow;
} 
//如果是带头结点的话将快慢指针修改为 fast = slow = head -> next即可;

  • 时空复杂度: O ( n ) / O ( 1 ) O(n)/O(1) O(n)/O(1)

扩展题：如果题目要2095. 删除链表的中间节点，那么可以设置一个pre指针一直保持在slow指针的前面一位，找到后执行删除结点操作就可以啦，代码如下：

//不带头结点
ListNode* deleteMiddle(ListNode* head) {
        if(head -> next == NULL) return NULL;
        ListNode *fast = head, *slow = head, *pre = head;
        while(fast && fast -> next) {
            pre = slow;
            slow = slow -> next;
            fast = fast -> next -> next;
        }
        pre -> next = slow -> next;
        delete(slow);
        return head;
}
  1. 环形链表

  • 题目:给你一个链表的头节点 head ，判断链表中是否有环。

    如果链表中存在环 ，则返回 true 。 否则，返回 false 。

  • 解题思路:设置快慢指针;快慢指针的特性 —— 每轮移动之后两者的距离会加一。当一个链表有环时，快慢指针都会陷入环中进行无限次移动，然后变成了追及问题。想象一下在操场跑步的场景，只要一直跑下去，快的总会追上慢的。当两个指针都进入环后，每轮移动使得慢指针到快指针的距离增加一，同时快指针到慢指针的距离也减少一，只要一直移动下去，快指针总会追上慢指针。

    快慢指针在环上追及

    bool hascycle(LNode *head) {
    LNode *fast = head, *slow = head;
    while(fast && fast -> next) {
        fast = fast -> next -> next;
        slow = slow -> next;
        if(fast = slow) {
            return true;
        }
    }
    return false;
}
  1. 环形链表 II

  • 题目:给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。不允许修改 链表。

  • 解题思路:如下图,设置快慢指针,当二者相遇后,再让头结点指针和慢指针同步向后移动,当二者相遇时,此时第二个相遇点就是环的入口处;证明如下:

  • 代码:

    //不带头结点的版本:
LNode* detectCycle(LNode *head) {   //head即链表的第一个结点
    LNode *fast = head, *slow = head;
    while(fast && fast -> next) {
        fast = fast -> next -> next;
        slow = slow ->  next;
        if(fast == slow) {     //第一次快慢指针相遇点;
            while(head != slow) {      //如果头指针和慢指针相遇,说明此时二者都到了环的入口处;
                head = head -> next;
                slow = slow -> next;
            }
            return slow;
        }
    }
    return NULL;
}

//带头结点的版本;
LNode* detectCycle(LNode *head) {     //此时head指向链表的头结点,数据域为空
    LNode *fast = head -> next, *slow = head ->  next;
    while(fast && fast -> next) {
        fast = fast -> next -> next;
        slow = slow ->  next;
        if(fast == slow) {     //第一次快慢指针相遇点;
            LNode * p = head -> next;
            while(p != slow) {      //如果p指针和慢指针相遇,说明此时二者都到了环的入口处;
                p = p -> next;
                slow = slow -> next;
            }
            return slow;
        }
    }
    return NULL;
}
    image-20230727131604808

快慢指针相遇时，为什么慢指针的移动距离小于环长？：考虑最坏的情况,慢指针进入环时,快指针刚好在它前面一位,因为二者的相对速度差为1,因此快指针需要走(环长-1)次二者相遇,其他情况快指针需要走的次数都比这种情况需要走的少,即慢指针走的次数也一定比(环长-1)少,因此慢指针移动距离一定小于环长.

力扣评论区解释：为何慢指针第一圈走不完一定会和快指针相遇： 首先，第一步，快指针先进入环 第二步：当慢指针刚到达环的入口时，快指针此时在环中的某个位置(也可能此时相遇) 第三步：设此时快指针和慢指针距离为x，若在第二步相遇，则x = 0； 第四步：设环的周长为n，那么看成快指针追赶慢指针，需要追赶n-x； 第五步：快指针每次都追赶慢指针1个单位，设慢指针速度1/s，快指针2/s，那么追赶需要(n-x)s 第六步：在n-x秒内，慢指针走了n-x单位，因为x>=0，则慢指针走的路程小于等于n，即走不完一圈就和快指针相遇

  1. 环形链表扩展题,求解环的长度

  • 解题思路:当快慢指针相遇时,继续移动,因为二者的相对速度差为1,因此到了第二次相遇时,两次相遇之间的移动次数就是环的长度;如果继续扩展的话,求整个链表的结点数的话,需要用上题的思路统计head指针移动到环的入口处移动的次数+环长即可(注意入环处的结点不要重复计数);

    //不带头结点版本;
int  LengthCycle(LNode *head) {
    LNode *fast = head, *slow = head;
    while(fast && fast -> next) {
        fast = fast -> next -> next;
        slow = slow -> next;
        if(fast = slow) {       //第一次相遇
            fast = fast -> next -> next;
            slow = slow -> next;
            int length = 1;
            while(fast != slow) {     
                fast = fast -> next -> next;
                slow = slow -> next;  
                length ++;
            }
            return length;    //第二次相遇,跳出循环;
        }
    }
}

    求解整个环形链表的结点数代码略,思路已给;

  1. 真题: 重排链表

  • 题目描述:给定一个单链表 L 的头节点 head ，单链表 L 表示为：

    L0 → L1 → … → Ln - 1 → Ln

    请将其重新排列后变为：

    L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …

    不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

  • 解题方法:本题考察了快慢指针找中间结点/链表的原地逆置(反转链表)/链表的交叉连接三个重要手法,题目不难但是代码量大,对基础要求高;

    class Solution {
    ListNode *middleNode(ListNode *head) {    //求中间结点;
        ListNode* slow = head, *fast = head;
        while(fast && fast -> next) {
            fast = fast -> next -> next;
            slow = slow -> next;
        }
        return slow;
    }

    ListNode *reverseList(ListNode* head) {    //将链表的后半段原地逆置
        ListNode *pre = NULL, *cur = head;
        while(cur) {
            ListNode* next = cur -> next;
            cur -> next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }

    
public:
    void reorderList(ListNode* head) {       //交叉链接
        ListNode *middle = middleNode(head);
        ListNode *head2 = reverseList(middle);
        while(head2 -> next) {
            ListNode * next = head -> next;     //保存后继结点,为了后面更新结点做准备
            ListNode *next2 = head2 -> next;   //保存后继结点
            head -> next = head2;
            head2 -> next =next;
            head = next;
            head2 = next2;
        }
    }
};
    • 时间复杂度： O ( n ) O(n) O(n)，其中 n n n为链表节点个数。
    • 空间复杂度： O ( 1 ) O(1) O(1)，仅用到若干额外变量。

  • 本题也有暴力解版本,把链表放进数组中，然后通过双指针法，一前一后，来遍历数组，构造链表。

    class Solution {
public:
    void reorderList(ListNode* head) {
        vector<ListNode*> vec;
        ListNode* cur = head;
        if (cur == nullptr) return;
        while(cur != nullptr) {
            vec.push_back(cur);
            cur = cur->next;
        }
        cur = head;
        int i = 1;
        int j = vec.size() - 1;  // i j为之前前后的双指针
        int count = 0; // 计数，偶数去后面，奇数取前面
        while (i <= j) {
            if (count % 2 == 0) {
                cur->next = vec[j];
                j--;
            } else {
                cur->next = vec[i];
                i++;
            }
            cur = cur->next;
            count++;
        }
        if (vec.size() % 2 == 0) { // 如果是偶数，还要多处理中间的一个
            cur->next = vec[i];
            cur = cur->next;
        }
        cur->next = nullptr; // 注意结尾
    }
};
    1. 回文链表

    • 题目描述:给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

    • 示例:img,返回true;img,返回false;

    • 解题思路:跟上题一样,先用快慢指针找到中间结点,然后将后半段逆置,再设置一个指针指向第一个结点,让它和指向中间结点的指针同时同速向表尾方向移动,边移动边比较节点值是否相等,若不相等则跳出循环返回false,若一直遍历结束都没有跳出循环,说明该链表是回文链表.

    • 注意后半段反转以后是这样的，也可以将链表断连一分为二，然后比较，但是只是单纯判断链表是否回文的话我觉得没有必要，我这样处理的话可以比较到中间结点结束即p == middle时结束，但是注意当链表为[1,2]这种情况的话会出错，即有特殊情况要处理，所以不妨直接比较到p为NULL时结束。

      image-20230726105337465 
      class Solution {
    ListNode *middleNode(ListNode *head) {    //求中间结点模板;
        ListNode* slow = head, *fast = head;
        while(fast && fast -> next) {
            fast = fast -> next -> next;
            slow = slow -> next;
        }
        return slow;
    }

    ListNode *reverseList(ListNode* head) {    //反转链表模板
        ListNode *pre = NULL, *cur = head;
        while(cur) {
            ListNode* next = cur -> next;
            cur -> next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }

public:
    bool isPalindrome(ListNode* head) {
        ListNode* middle = middleNode(head);   //求中间结点；
        ListNode* p =  reverseList(middle);    //将链表后半段逆置
        while(p){       //下面开始依次比较节点值是否相等；
            if(p -> val != head ->val ){
                return false;
            }
            p = p -> next;
            head = head -> next;
        }
        return true;
    }
};

      时空复杂度： O ( n ) / O ( 1 ) O(n)/O(1) O(n)/O(1)

    • 其他方法:

      1. 由于数组具有随机访问的性质,可以考虑复制链表结点数值到数组中,然后用双指针法判断是否为回文链表;

        class Solution {
public:
    bool isPalindrome(ListNode* head) {
        vector<int> vals;
        while (head != NULL) {
            vals.push_back(head->val);
            head = head->next;
        }
        for (int i = 0, int j = vals.size() - 1; i < j; ++i, --j) {
            if (vals[i] != vals[j]) {
                return false;
            }
        }
        return true;
    }
};

      2. 可以考虑用栈来做,将该链表所有结点值遍历输入到栈中,再依次弹出和链表元素比较;因为是回文所以链表反过来和正过来一模一样，用stack做很方便

        class Solution {
    public boolean isPalindrome(ListNode head) {
        Stack<Integer> stack=new Stack<Integer>();
        ListNode cur=head;
        while(cur!=null){
            stack.push(cur.val);
            cur=cur.next;
        }
        while(head!=null){
            if(stack.pop()!=head.val)
                return false;
            head=head.next;
        }
        return true;
    }
}
//但是注意空间复杂度不符合O(1)的要求;

比较;因为是回文所以链表反过来和正过来一模一样，用stack做很方便

   ```cpp
   class Solution {
       public boolean isPalindrome(ListNode head) {
           Stack<Integer> stack=new Stack<Integer>();
           ListNode cur=head;
           while(cur!=null){
               stack.push(cur.val);
               cur=cur.next;
           }
           while(head!=null){
               if(stack.pop()!=head.val)
                   return false;
               head=head.next;
           }
           return true;
       }
   }
   //但是注意空间复杂度不符合O(1)的要求;
   ```

标签：结点,线性表,head,fast,next,链表,第二章,cur
From： https://blog.csdn.net/m0_72520040/article/details/139101500

相关文章

  • CSAPP第二章
    gcc指定不同的C语言版本 注意寻址和字节顺序讲的, 对象的地址都是从小地址开始算起, 而所谓大端法就是高位字节在前; 小端法则是低位字节在前注意: 等号上的小圆点的组合表示"被定义为"的意思 反码有+0和-0,-0就是全为1的位模式,负数的反码就是对应正数所有位取反......
  • 分布式数据处理-《Spark编程基础》（Scala版）第二章简答题答案（自制）
    2Scala语言基础简答题T1简述Scala语言与Java语言的联系与区别。答：①联系：（1）Scala和Java均运行在JVM之上；（2）Scala和Java均有面向对象语言特点；②区别：（1）Scala是类Java的多范式编程；Java是命令式编程。T2简述Scala语言的基本特性。......
  • 第二章复习
    二、软件质量管理1.软件质量的定义。      质量是产品或者服务满足明确或隐含需要能力的性能和特性的总体      软件质量是软件产品满足明确或隐含需要能力的性能和特性的总体。2.ISO/IEC9126的结构、六个一级质量特性、一级特性对应的二级特性（理解）。功能......
  • 查找 - 线性表 & 散列表 & 树
    线性表的查找顺序查找技巧：设置哨兵，放在下标为0的位置。intSearch_Seq(SSTableST,KeyTypekey){ST.R[0].key=key;for(inti=ST.length;ST.R[i].key!=key;i--);returni;}算法分析适用于顺序结构和链式结构，不要求记录按关键字有序。平均查找长度......
  • 10.5线性表的链式存储
    链表顺序表：缺点1、插入和删除操作移动大量元素。2、数组大小不好确定。3、占用空间。优点随机访问逻辑相邻物理位置上也相邻单链表（逻辑上相邻物理不相邻）链表定义：typedefintElemtype;structLNode{ Elemtypedata;//数据域 structLNode*next;//指针域};优点1......
  • 线性表
    数据结构代码--线性表#defineN10typedefstructNode{ intdata; structNode*next;}NODE;intGet_Data(inti); //定义省略Node*Create_u(){ inti; NODE*p,*Head=NULL; for(i=0;i<N;i++) {   VP=NewNODE;   P->Data=Get_Data(i); ___......
  • 【第二章】利用用户行为数据
    基于用户行为分析的推荐算法是个性化推荐系统的重要算法，学术界一般将这种类型的算法称为协同过滤算法。顾名思义，协同过滤就是指用户可以齐心协力，通过不断地和网站互动，使自己的推荐列表能够不断过滤掉自己不感兴趣的物品，从而越来越满足自己的需求。2.1用户行为数据简介一般来说，......
  • 王道数据结构个人向笔记-第二章（线性表）
    目录2.1线性表的定义和基本操作2.2顺序表2.2.1顺序表的定义2.2.2顺序表的插入、删除（实现是基于静态分配）2.2.3顺序表的查找2.3链表2.3.1单链表的定义2.3.2单链表的插入删除2.3.3单链表的查找2.3.4单链表的建立2.3.4双链表2.3.5循环链表2.3.6静态链表2.3.7顺序表和链......
  • 第二章 标准数据类型
    1.六大标准数据类型1.1Number(数字类型)#(1)int整型(正整型,0,负整形)#二进制整型intvar=0b110#八进制整型intvar=0o127#十进制整型intvar1=100intvar2=0intvar3=-10#十六进制整型intvar=0xff#(2)float浮点型（小数）#表达式1floatvar=3.6#......
  • 第二章：Coherence Basics
    chapter2：coherence基础在本章将充分介绍cachecoherence，以了解一致性模型如何与缓存交互。2.1节开始介绍贯穿本书的系统模型。第2.2节解释了必须解决的缓存一致性问题以及不一致性的可能性是如何产生的。第2.3节精确地定义了缓存一致性1、基准系统模型（BaselineSystemmodel）基......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99