高精度

洛谷P2437 蜜蜂路线

蜜蜂路线

题目背景

无

题目描述

一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房 $m$ 开始爬到蜂房 $n$，$m<n$，有多少种爬行路线？（备注：题面有误，右上角应为 $n-1$）

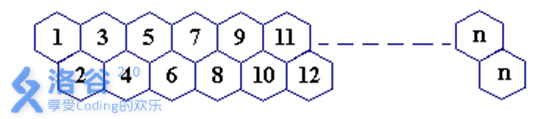
输入格式

输入 $m,n$ 的值

输出格式

爬行有多少种路线

样例 #1

样例输入 #1

1 14

样例输出 #1

377

提示

对于100%的数据，$1 \le M,N\le 1000$

这题是一道简单的求斐波那契数列题，但由于题目所给数字比较大，所以需要用到高精度。

主要代码

void fun() {
    for(int i = 0; i <= length; i++) {
        re[now][i] = re[now-1][i] + re[now-2][i];
    }

    for(int i = 0; i <= length; i++) {
        if(re[now][i] >= 10) {
            re[now][i+1] += re[now][i]/10;
            re[now][i] %= 10;
        }
    }
    if(re[now][length+1]) length++;
    now++;
}

1. 第一个循环先按位相加
2. 第二个循环判断每一位是否大于10，如果大于10，进位re[now][i+1] += re[now][i]/10;，然后剩下个位re[now][i] %= 10;
3. 由于高位存储于下标高的数组中，所以需要反向循环输出

    for(int i = length; i >= 0; i--) {
        cout << re[now-1][i];
    }

注意事项

• 需要一个length作为已经记录的最高位，每次判断更高位是否有数增加最高位if(re[now][length+1]) length++;
• 由于数组初始化为0，因此判断最高位方法正确
• 如果两个数最高位不同，a的最高位大于b，之前已经有了最高位的更新if(re[now][length+1]) length++;所以a的最高位为length或length+1，a+b最高位同样如此

完整代码如下

#include <bits/stdc++.h>
using namespace std;

int re[1000][1000] = {0};
int now = 0, length = 0;

void fun() {
    for(int i = 0; i <= length; i++) {
        re[now][i] = re[now-1][i] + re[now-2][i];
    }

    for(int i = 0; i <= length; i++) {
        if(re[now][i] >= 10) {
            re[now][i+1] += re[now][i]/10;
            re[now][i] %= 10;
        }
    }
    if(re[now][length+1]) length++;
    now++;
}

int main() {
    int m, n;
    cin >> m >> n;
    n = n-m+1;
    m = 1;
    re[1][0] = 1;
    re[2][0] = 1;
    now = 3;
    for(int i = 3; i <= n; i++) {
        fun();
    }
    for(int i = length; i >= 0; i--) {
        cout << re[now-1][i];
    }
}