\(\color{#F39C11}(1)\) CF1941B Rudolf and 121
给定一个长度为 \(n\) 的序列 \(a\)。求最少进行多少次操作后所有 \(a_i = 0\):
- 选择一个 \(2 \le i < n\),并让 \(a_i \gets a_i - 2, a_{i - 1} \gets a_{i - 1} - 1, a_{i + 1} \gets a_{i + 1} - 1\)。
我们记选择 \(i = x\) 时的操作为 \(\operatorname{opt}(x)\)。
发现 \(a_1\) 只有 \(\operatorname{opt}(2)\) 才会发生变化。也就是说我们只能通过若干次 \(\operatorname{opt}(2)\) 才能使 \(a_1 = 0\)。所以 \(\operatorname{opt}(2)\) 需要做 \(a_1\) 次。
此时 \(a_1 = 0\)。
同理,对于 \(a_2\),显然我们不能选择 \(\operatorname{opt}(1)\) 或 \(\operatorname{opt}(2)\)。因为这两种操作都会使 \(a_1\) 变小。所以此时能影响到 \(a_2\) 的只有 \(\operatorname{opt}(3)\)。
同理依次操作 \(\operatorname{opt}(i), i = (2, 3, 4, \dots, n - 1)\)。然后判断所有元素是否均为 \(0\) 即可。
时间复杂度 \(\Theta(n)\)。
$\color{blue}\text{Code}$
void Luogu_UID_748509() {
int n; fin >> n;
vector<int> a(n);
fin >> a;
for (int i = 0; i + 2 < n; ++ i ) {
if (a[i] < 0) {
puts("NO");
return;
}
a[i + 1] -= a[i] * 2;
a[i + 2] -= a[i];
a[i] = 0;
}
puts(a[n - 2] || a[n - 1] ? "NO" : "YES");
}
\(\color{#FFC116}(2)\) CF1941D Rudolf and the Ball Game
有 \(n\) 个人围成一圈。最开始第 \(x\) 个人拿着一个球。
接下来会发生 \(m\) 个事件,每个事件形如 \((r_i, c_i)\),其中:
- \(c_i = \texttt 0\) 表示当前手中有球的人将球顺时针传给第 \(x_i\) 个人。
- \(c_i = \texttt 1\) 表示当前手中有球的人将球逆时针传给第 \(x_i\) 个人。
- \(c_i = \texttt ?\) 表示这个事件不清楚,当前手中有球的人将球顺时针或逆时针传给第 \(x_i\) 个人。
求最终哪些人可能有球。
我们设 bool 状态 \(f_{i, j}\) 表示第 \(i\) 个事件结束后,第 \(j\) 个人是否有可能拿着球。开始 \(f_{0, x} = \text{true}\)。
转移极易,我们令 \(F(x, y)\) 表示从 \(x\) 顺时针第 \(y\) 个人的编号,\(G(x, y)\) 表示从 \(x\) 逆时针第 \(y\) 个人的编号。那么有
\[f_{i + 1, F(j, r_i)} = f_{i +1 , G(j, r_i)} = f_{i, j} \]最后看哪些 \(j\) 满足 \(f_{n, j} = \text{true}\) 即可。
时空复杂度均 \(\Theta(nm)\)。当然可以滚动数组将空间复杂度优化成 \(\Theta(m)\)。
$\color{blue}\text{Code}$
int n, m, x;
int dis;
char op;
bool st[110][N];
int F(int a, int b) {
return ((a + b) % n + n) % n;
}
void Luogu_UID_748509() {
fin >> n >> m >> x;
// for (int j = 0; j <= m; ++ j )
for (int i = 0; i < n; ++ i )
st[0][i] = st[1][i] = 0;
st[0][x - 1] = true;
for (int j = 1; j <= m; ++ j ) {
cin >> dis >> op;
for (int i = 0; i < n; ++ i )
if (st[j - 1 & 1][i]) {
if (op != '1') st[j & 1][F(i, dis)] = true;
if (op != '0') st[j & 1][F(i, -dis)] = true;
st[j - 1 & 1][i] = 0;
}
}
int res = 0;
for (int i = 0; i < n; ++ i ) res += st[m & 1][i];
fout << res << '\n';
for (int i = 0; i < n; ++ i ) if (st[m & 1][i]) fout << i + 1 << ' ';
puts("");
}
\(\color{#52A41A}(3)\) CF1941E Rudolf and k Bridges
有一条 \(n \times m\) 的河。第 \(i\) 行第 \(j\) 列的深度为 \(a_{i, j}\)。保证 \(a_{i, 1} = a_{i, m} = 0\)。
如果在第 \(i\) 行第 \(j\) 列安置桥墩,所需代价为 \(a_{i, j} + 1\)。
你需要选择连续的 \(k\) 行,每行都要架起若干个桥墩,并满足以下条件:
- 每行的第 \(1\) 列必须架桥墩;
- 每行的第 \(m\) 列必须架桥墩;
- 每行的相邻两个桥墩的距离不超过 \(d\)。其中 \((i, j_1)\) 和 \((i, j_2)\) 之间的距离为 \(|j_1 - j_2| - 1\)。
求最小代价和。
行与行之间架桥墩并无关系。我们可以求出第 \(i\) 行所需的最小代价 \(g(i)\),那么 \(\min_{i=1}^{n-k+1}\sum_{j=i}^{i+k-1}g(j)\) 即为答案。
对于每一行分别 DP,当前是第 \(r\) 行。设状态 \(f(i)\) 表示若只考虑前 \(i\) 列,且第 \(i\) 列一定架桥,所需的最小代价和。转移枚举上一个桥墩的位置,即:
\[f(i) = a_{r, i} + 1 + \min_{j=i-k-1}^{i - 1} f(j) \]发现后面的 \(\min_{j=i-k-1}^{i - 1} f(j)\) 可以非常容易地用数据结构维护,例如单调队列或线段树。
总时间复杂度为 \(\Theta(nm\log m)\),用线段树实现的。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
#define int long long
typedef long long ll;
typedef unsigned long long LL;
typedef pair<int, int> PII;
struct FASTREAD {
template <typename T>
FASTREAD& operator >>(T& x) {
x = 0; bool flg = false; char c = getchar();
while (c < '0' || c > '9') flg |= (c == '-'), c = getchar();
while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
if (flg) x = -x; return *this;
}
template <typename T>
FASTREAD& operator >>(vector<T>& x) {
for (auto it = x.begin(); it != x.end(); ++ it ) (*this) >> *it;
return *this;
}
}fin;
struct FASTWRITE {
template <typename T>
FASTWRITE& operator <<(T x) {
if (x < 0) x = -x, putchar('-');
static int buf[35]; int top = 0;
do buf[top ++ ] = x % 10, x /= 10; while (x);
while (top) putchar(buf[ -- top] + '0');
return *this;
}
FASTWRITE& operator <<(char x) {
putchar(x); return *this;
}
template <typename T>
FASTWRITE& operator <<(vector<T> x) {
for (auto it = x.begin(); it != x.end(); ++ it ) (*this) << *it, putchar(' ');
putchar('\n');
return *this;
}
}fout;
const int N = 110, M = 2e5 + 10;
const int P = 998244353;
int n, m, k, d;
int a[N][M];
int sum[N];
int f[M];
struct Tree {
int l, r, v;
}tr[M << 2];
void pushup(int u) {
tr[u].v = min(tr[u << 1].v, tr[u << 1 | 1].v);
}
void build(int u, int l, int r) {
tr[u] = {l, r, 0};
if (l == r) tr[u].v = 0;
else {
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
}
}
void modify(int u, int x, int d) {
if (tr[u].l == tr[u].r) tr[u].v += d;
else {
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(u << 1, x, d);
else modify(u << 1 | 1, x, d);
pushup(u);
}
}
int query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int mid = tr[u].l + tr[u].r >> 1, res = 1e18;
if (l <= mid) res = query(u << 1, l, r);
if (r > mid) res = min(res, query(u << 1 | 1, l, r));
return res;
}
void Luogu_UID_748509() {
fin >> n >> m >> k >> d;
for (int i = 1; i <= n; ++ i ) {
for (int j = 1; j <= m; ++ j ) fin >> a[i][j];
build(1, 1, m);
f[1] = a[i][1] + 1;
modify(1, 1, f[1]);
for (int j = 2; j <= m; ++ j ) {
f[j] = a[i][j] + 1 + query(1, max(1ll, j - d - 1), j - 1);
modify(1, j, f[j]);
}
sum[i] = sum[i - 1] + f[m];
}
int res = 1e18;
for (int l = 1, r = k; r <= n; ++ l, ++ r ) res = min(res, sum[r] - sum[l - 1]);
fout << res << '\n';
return;
}
signed main() {
int Testcases = 1;
fin >> Testcases;
while (Testcases -- ) Luogu_UID_748509();
return 0;
}
\(\color{#FFC116}(4)\) CF1945D Seraphim the Owl
有 \(n + 1\) 个人站成一排,最开始第 \(i\) 个人在位置 \(i\) 上。
你是第 \(n + 1\) 个人。除你之外,每个人都有两个属性 \(a_i, b_i\)。
每次操作时,假如你在位置 \(i\) 上,那么你需要选择一个位置 \(1 \le j < i\) 并和位置 \(j\) 的人交换位置。代价为 \(a_j + \sum_{k = j + 1}^{i - 1}b_k\)。
求若你最终移动到的位置小于等于 \(m\),总代价最小是多少。
假如我们可以求出 \(f_i\) 表示你从 \(n + 1\) 到达 \(i\) 的最小代价,那么答案即 \(\min_{i = 1}^m f_i\)。
我们可以画图模拟一下跟前面人交换位置的过程:
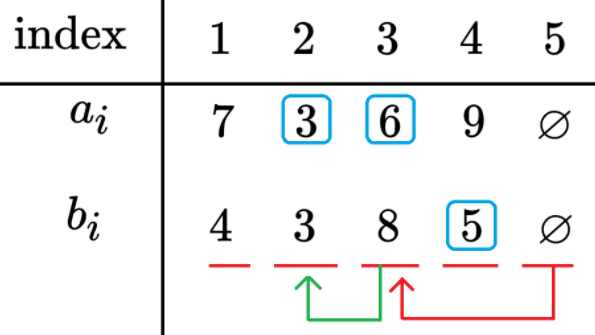
那么答案为蓝色框起的数之和 \(3 + 6 + 5 = 14\)。
可以发现,若某个人 \(j\) 是和你交换过位置的,那么 ta 的贡献为 \(a_i\)。否则若是被你跨过的,ta 的贡献为 \(b_i\)。
每个人是否选择和你交换是你可以选择的,所以对于每个人,我们看两种方式的代价 \(a_i\) 和 \(b_i\) 的大小,并取代价较小的方案即可。
回到我们求解 \(f_i\) 的任务。由于我们最终到了位置 \(i\) 上,所以我们必定会和第 \(i\) 个人交换位置。那么实际上我们一定会消耗代价 \(a_i\)。但是对于后面的人,就可以用上面的策略进行了。所以 \(f_i = a_i + \sum_{j=i+1}^n \min(a_j, b_j)\)。
$\color{blue}\text{Code}$
int n, k, a[N], b[N], suf[N], p[N];
void Luogu_UID_748509() {
fin >> n >> k;
for (int i = 1; i <= n; ++ i ) fin >> a[i];
for (int i = 1; i <= n; ++ i ) fin >> b[i];
a[n + 1] = b[n + 1] = 0;
suf[n + 1] = p[n + 1] = 0;
for (int i = n; i; -- i ) {
suf[i] = suf[i + 1] + min(a[i], b[i]);
p[i] = suf[i + 1] + a[i];
}
fout << *min_element(p + 1, p + k + 1) << '\n';
return;
}