Link。
0x01 进制
引入
计数原理,对于 \(N\) 进制,那么就是逢 \(N\) 进一。
计算机中常用二进制,对应电路中的通电(\(1\))断电(\(0\))。
人类从远古以来使用十进制。
常用的有二进制、三进制、八进制、十进制、十六进制等。
由于不同进制之间数值写法可能相同,在没有特殊说明下默认为十进制。
对于 \(m\) 进制数 \(n\),表示为 \((n)_m\)。
在 OI 中的应用例如位运算、lowbit、状压dp等。
经常考察的是进制之间的转换。
十进制转 \(N\) 进制
描述
使用短除法。
对于正整数 \(n\),将它转成 \(m\) 进制。
对 \(n\) 整除 \(m\),并记下 \(n\bmod m\),直到 \(n=0\),倒序输出 \(n\bmod m\)。\(\div\)
例如将 \((13)_{10}\) 转成二进制,整个过程如下:
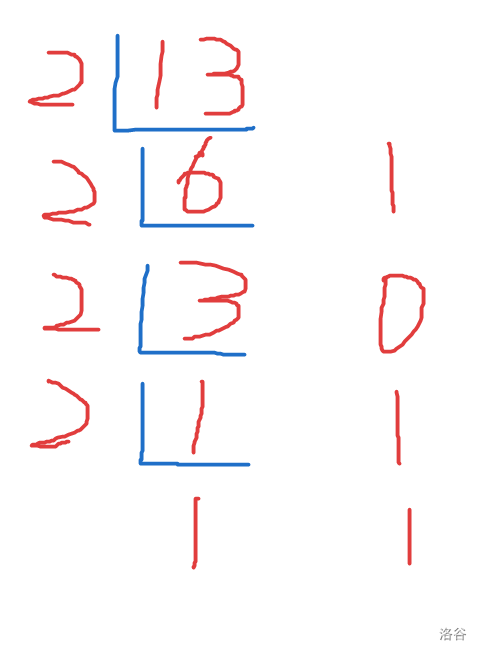
那么 \((13)_{10}=(1101)_2\),转换完毕。
例题
\(N\) 进制转十进制
描述
一个 \(m\) 进制数 \(n\),将它转为十进制。
假设 \((n)_m\) 有 \(t\) 位,第 \(i\) 位是 \(n_i\),那么转为十进制后是 \(\sum_{i=0}^{t-1}{n_i\times m^i}\)
例如将 \((1101)_2\) 转为十进制,过程如下:

那么 \((1101)_2=(13)_{10}\),转换完毕。