题解 UOJ577【[ULR #1] 打击复读

reference

https://www.cnblogs.com/crashed/p/17382894.html

https://www.cnblogs.com/sizeof127/articles/17579027.html

字符串——黄建恒，广东实验中学

题目描述

为了提升搜索引擎的关键词匹配度以加大访问量，某些网站可能在网页中无意义复读大量关键词。

你设计了一种方法量化评价一个文本（字符串 $s$）的“复读程度”：

字符串 $s$ 的下标从 $1\sim n$ 标号，第 $i$ 个字符被赋予两个权值：左权值 $wl_i$ 和右权值 $wr_i$ ，代表该位置的重要度。

定义一个子串 $s[l,r]$ 的左权值 $vl(s[l,r])$ 为：其在原串中各个匹配的左端点的左权值 $wl$ 和；右权值 $vr(s[l,r])$ 为：其在原串中各个匹配的右端点的右权值 $wr$ 和。这里 $t$ 在 $s$ 中所有的匹配是 $\forall 1 \le i \le j \le n,s[i,j]=t$，我们把这样的 $i$ 和 $j$ 分别叫做一个匹配的左右端点。

定义一个子串 $s[l,r]$ 的复读程度是它的左权值与右权值的乘积，即 $w(s[l,r])=vl(s[l,r])\cdot vr(s[l,r])$ 。

$s$ 的“复读程度”定义为所有子串复读程度的和，即：

$$\sum\limits_{i=1}^{|S|}\sum\limits_{j=i}^{|S|}w(s[i,j]).$$

根据网站文本抽样的复读程度限流，就可以达到打击无意义复读行为的目的。

隔壁生命科学实验室正在分析跳蚤的基因序列。他们对基因的复读情况很感兴趣，于是顺便把这个锅丢给了你。

基因片段可以被视作字符集为 $\{A,T,G,C\}$ 的字符串，你要求出给定的基因片段 $S$ 的复读程度。

有些时候，由于新的科学发现，某个位置 $u$ 的左权值 $wl_u$ 会相应修改为 $v$，修改过后你需要给出基因片段 $S$ 的新的复读程度。

由于答案很大，你只需要输出答案对 $2^{64}$ 取模后的结果。

对于所有数据，满足 $1\leq n,m\leq 5\times 10^5,0\leq wl_i,wr_i,v_i< 2^{64},1\leq u_i\leq n$。

基本子串结构

概念

你现在有一个巨大的字符串 \(S=\{S_1, S_2, \cdots, S_n\}\)。在上面，定义了 \(occ(s)\) 表示一个小字符串 \(s\) 在 \(S\) 中的出现次数。

定义 \(ext(s)\) 为一个最长的串满足 \(occ(ext(s))=ext(s)\)，容易发现它存在且唯一。容易发现 \(ext(ext(s))=ext(s)\)，由此将 \(ext(s)\) 相同的 \(s\) 拿出来（都是 \(S\) 的子串）称为一个等价类，\(ext(s)=s\) 的 \(s\) 为等价类的代表元。

以 \(l\) 为横坐标，\(r\) 为纵坐标，建立平面直角坐标系，一个点 \((l, r)\) 代表一个子串 \(S[l:r]\)。将所有等价类在直角坐标系中画出来，发现：

• 同一个代表元对应的等价类会在图中出现 \(occ()\) 次。

  以下所有讨论，没有说明，都是一个本质不同代表元值讨论其中一个对应等价类。

  （对应的在 SAM 中的等价类概念改成为”状态“）

• 所有等价类，都形成了阶梯型，左上角为阶梯的角，左上对齐，右下阶梯型。

  这是基于 \(ext(S[l:r])=S[L:R]\implies ext(S[l':r'])=S[L, R](L\leq l'\leq l\leq r\leq r'\leq R)\) 这个直观的结论。

例子的来源是第一篇参考资料。字符串 aababcd 的等价类形态如图所示。同色的是一个等价类。

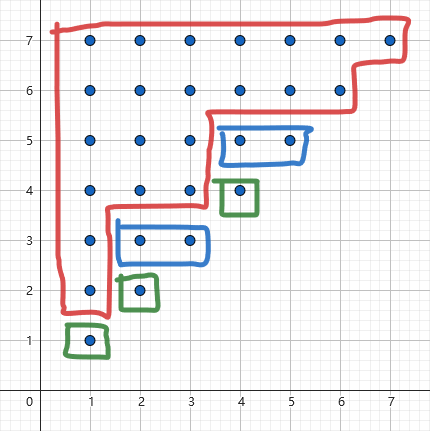
对应 SAM

每个等价类的一行的 \(r\) 相同，代表了正串 SAM 的一个状态，也即行等价类；每个等价类的一列的 \(l\) 相同，代表了反串 SAM 的一个状态，也即列等价类；本质相同的行等价类或列等价类对应的状态相同。

将每一行对应正 SAM 一个状态，每一列对应反 SAM 一个状态，则所有本质不同等价类的周长和为 \(O(n)\)。

以正 SAM 为例，对一个行等价类与其对应的状态 \(u\)。状态 \(u\) 跳满足 \(len_u+1=len_v, v\in ch_u\) 的 DAG 转移边代表行等价类向上跳（这里有个分讨：如果这个行等价类是代表元，则向上跳会跳到其他若干个等价类的底部；否则只有一个出边，跳到它上面一行。现在说明为什么非代表元只有一个出边，因为首先由 \(occ()\) 相同，向上的这一条边必然存在，然后如果有其它的边，\(occ(u)\) 与其上一行的 \(occ()\) 就不能相等了。例如 \(s,s+c, s+d\) 都存在，那么如果 \(occ(s)=occ(s+c)\)，将 \(occ(s+d)\) 抠掉 \(d\) 之后剩下的一堆 \(s\) 的出现后面都是 \(d\)，而不是 \(c\)，\(occ(s)\) 就会凭空多出一些。）

状态 \(u\) 跳后缀链接 \(link_u\)，代表行等价类往右走，因为它们都有相同的这个行也就是 \(rpos\) 也就是 \(endpos\)。（明显看出这个不严谨，摆烂了）

反 SAM 就是反的，列等价类向左或者向下。

SAM 前插字符

为了铺垫下文引入这个技巧。考虑在正 SAM 上匹配字符串的过程，如果现在跑到状态 \(u\)，匹配长度 \(l\)，那么怎么在前面插入字符 \(r\) 呢？首先确定是要在后缀链接上搞事情，然后：

• 若 \(l =len_u\)，即将要向后缀链接树上的一个儿子走，考虑这个儿子是 \(son[u][r]\)，我们需要对每个状态都 \(son[link_u][S[pos_u-len_{link_u}]]\) 其中 \(pos_u\) 是 \(u\) 任意一个 endpos（插入的时候记一个，复制的时候复制过去），这样就是说在考虑 \(pos_u\) 这一 endpos 的时候将 \(u\) 代表的最短串的第一个字符拿出来，相当于就是后缀链接树上走下去第一个字符，然后就对了。
• 否则判断是否有 \(S[pos_u-l]=r\)，没有就失配，否则状态不变，长度 +1。

写的迷糊，参考 P4218 [CTSC2010] 珠宝商 这题题解。

建立结构

考虑同时建立正反串 SAM。识别代表元时，发现出边中 \(occ()\) 没有相同的就是代表元，它在保留 \(len_u+1=len_v\) 边的 DAG 的头上会有一条链，是这个等价类的行等价类或列等价类。然后对应另一个 SAM，只需要将其在另一个 SAM 上定位，或者采取以下做法：

• dfs(x, y, l) 表示正在对应正 SAM 上 \(x\)，反 SAM 上 \(y\)，目前长度为 \(l\)。

• 记正 SAM 为 \(ms\)，反 SAM 为 \(mr\)。若 \(ms.len_x=mr.len_y\)，找到代表元，记录一下。

  这里说明为什么一定是，这个意思是在进入新的等价类时，\(x\) 一直向上跳，\(y\) 因为跳后缀链接 \(l\) 不够一直不动，\(ms.len_x\) 在增，\(mr.len_y\) 不动且 \(ms.len_x\leq mr.len_y\)，取等时就找到了代表元。

• 然后遍历所有 \(ms.len_x+1=ms.len_v\) 出边，在 \(y\) 前对应前插一个字符，如果都存在，那么 dfs 下去，长度 +1。

找到代表元以后，由于剩下的等价类已经划分为很多条链（而且甚至删掉代表元以后 DAG 不用删 \(len_u+1\neq len_v\) 都只有一条出边），直接倒拓扑序（编号倒序）遍历上传代表元，暴力记录等价类的所有行等价类与列等价类。

solution

建立基本子串结构。明显是求

code

#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
typedef long long LL;
typedef unsigned long long mint;
template <int N, int M>
struct suffixam {
  int ch[N << 1][M], tot, link[N << 1], len[N << 1], occ[N << 1], pos[N << 1];
  int pr[N << 1][M];
  suffixam() : tot(1) {
    len[1] = link[1] = 0;
    memset(ch[1], 0, sizeof ch[1]);
  }
  int split(int p, int q, int r) {
    if (len[q] == len[p] + 1) return q;
    int u = ++tot;
    len[u] = len[p] + 1;
    memcpy(ch[u], ch[q], sizeof ch[0]);
    link[u] = link[q];
    link[q] = u;
    pos[u] = pos[q];
    for (; p && ch[p][r] == q; p = link[p]) ch[p][r] = u;
    return u;
  }
  int stc[N + 10];
  int expand(int p, int r) {
    if (ch[p][r]) return split(p, ch[p][r], r);
    int u = ++tot;
    pos[u] = len[u] = len[p] + 1;
    stc[len[u]] = r;
    memset(ch[u], 0, sizeof ch[u]);
    for (; p; p = link[p]) {
      if (ch[p][r]) {
        link[u] = split(p, ch[p][r], r);
        return u;
      } else {
        ch[p][r] = u;
      }
    }
    link[u] = 1;
    return u;
  }
  template <bool rev>
  vector<int> bucketsort() {
    vector<int> per(tot), buc(tot + 1);
    for (int i = 1; i <= tot; i++) buc[len[i]] += 1;
    for (int i = 1; i <= tot; i++) buc[i] += buc[i - 1];
    for (int i = 1; i <= tot; i++) per[--buc[len[i]]] = i;
    if (rev) reverse(per.begin(), per.end());
    return per;
  }
  int push_back(int u, int r, int l) {
    return ch[u][r];
  }
  int push_front(int u, int r, int l) {
    if (l == len[u]) return pr[u][r];
    return (stc[pos[u] - l] == r) * u;
  }
  int bel[N << 1];
};
int to_index(char t) {
  switch (t) {
    case 'A':
      return 0;
    case 'T':
      return 1;
    case 'G':
      return 2;
    case 'C':
      return 3;
  }
  throw "to_index: t is not in 'ATGC'";
}
int n, str[500010], blk, repr[1000010][2], inp[500010];
vector<int> sid[1000010], rid[1000010];
mint wl[500010], wr[500010], wrs[1000010], coe[1000010], tmp[1000010], hjh[500010];
suffixam<500010, 4> ms, mr;
void init() {
  for (int i = 1, lst = 1; i <= n; i++)
    ms.occ[lst = ms.expand(lst, str[i])] += 1, wrs[lst] += wr[i];
  for (int i = 1; i <= ms.tot; i++)
    ms.pr[ms.link[i]][ms.stc[ms.pos[i] - ms.len[ms.link[i]]]] = i;
  for (int i : ms.bucketsort<true>()) 
    ms.occ[ms.link[i]] += ms.occ[i], wrs[ms.link[i]] += wrs[i];
  for (int i = n, lst = 1; i >= 1; i--) 
    mr.occ[inp[i] = lst = mr.expand(lst, str[i])] += 1;
  for (int i = 1; i <= mr.tot; i++)
    mr.pr[mr.link[i]][mr.stc[mr.pos[i] - mr.len[mr.link[i]]]] = i;
  for (int i : mr.bucketsort<true>()) 
    mr.occ[mr.link[i]] += mr.occ[i];
  auto dfs = [&](auto& dfs, int x, int y, int len) -> void {
    if (ms.len[x] == mr.len[y]) {
      ms.bel[x] = mr.bel[y] = ++blk;
      repr[blk][0] = x, repr[blk][1] = y;
    }
    for (int r = 0; r < 4; r++) {
      int xv = ms.push_back(x, r, len), yv = mr.push_front(y, r, len);
      if (xv && yv && ms.len[xv] == ms.len[x] + 1) dfs(dfs, xv, yv, len + 1);
    }
  };
  dfs(dfs, 1, 1, 0);
  for (int u = ms.tot; u >= 1; u--) {
    if (!ms.bel[u]) {
      for (int r = 0; r < 4; r++) {
        if (ms.ch[u][r] && ms.len[u] + 1 == ms.len[ms.ch[u][r]]) { ms.bel[u] = ms.bel[ms.ch[u][r]]; break; }
      }
    }
    sid[ms.bel[u]].push_back(u);
  }
  for (int u = mr.tot; u >= 1; u--) {
    if (!mr.bel[u]) {
      for (int r = 0; r < 4; r++) {
        if (mr.ch[u][r] && mr.len[u] + 1 == mr.len[mr.ch[u][r]]) { mr.bel[u] = mr.bel[mr.ch[u][r]]; break; }
      }
    }
    rid[mr.bel[u]].push_back(u);
  }
  for (int id = 1; id <= blk; id++) {
    mint occ = ms.occ[repr[id][0]];
    tmp[0] = 0;
    for (int i = 1; i <= sid[id].size(); i++) tmp[i] = tmp[i - 1] + wrs[sid[id][i - 1]] * occ;
    auto getlen = [&](int u) { return mr.len[u] - mr.len[mr.link[u]]; };
    for (int i = 0; i < rid[id].size(); i++) coe[rid[id][i]] += tmp[getlen(rid[id][i])];
  }
  for (int i : mr.bucketsort<false>()) coe[i] += coe[mr.link[i]];
//for (int i = 1; i <= mr.tot; i++) for (int r = 0; r < 4; r++) if (mr.ch[i][r]) coe[mr.ch[i][r]] += coe[i], assert(mr.ch[i][r] > i);
  for (int i = 1; i <= n; i++) hjh[i] = coe[inp[i]];
}
int main() {
#ifndef LOCAL
  cin.tie(nullptr)->sync_with_stdio(false);
#endif
  int q;
  cin >> n >> q;
  for (int i = 1; i <= n; i++) {
    char ch;
    cin >> ch;
    str[i] = to_index(ch);
  }
  for (int i = 1; i <= n; i++) cin >> wl[i];
  for (int i = 1; i <= n; i++) cin >> wr[i];
  init();
  mint fans = 0;
  for (int i = 1; i <= n; i++) fans += wl[i] * hjh[i];
  cout << fans << endl;
  while (q--) {
    int i;
    mint v;
    cin >> i >> v;
    fans -= wl[i] * hjh[i];
    wl[i] = v;
    fans += wl[i] * hjh[i];
    cout << fans << endl;
  }
  return 0;
}