简介

字典树是一种用来维护多个字符串的前缀的数据结构，时空复杂度均为 \(O(\sum |S|)\)。

字典树是一颗外向树（边从父亲连向儿子），每条边的边权都为一个字符，一个结点对应的字符串为从根节点到当前结点的边的字符组成的字符串。

比如，当 \(N=5\)，\(S_1,S_2,\dots,S_5\) 分别为 ak、aoi、aer、i、ao 时字典树如下：

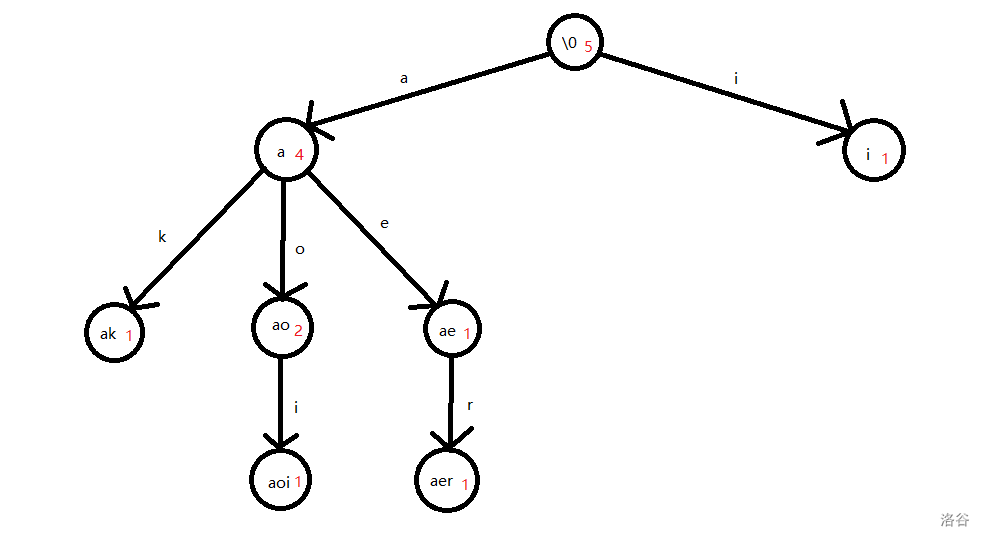
其中黑色的代表对应字符串，红色的代表这个字符串作为前缀的出现次数。

注：\0 指空字符。

插入

枚举字符串的每个字符，如果当前结点有一条边的字符等于当前字符，就走到对应儿子；否则就创建一个新结点并建边，再走到那个儿子。途中将经过的点的出现次数加 \(1\)。

单次时间复杂度 \(O(|S|)\)。

代码

void Insert(const string &s) {
  int u = 1;
  for(char c : s) {
    if(!son[u][c]) {
      son[u][c] = ++tot;
    }
    cnt[u]++;
    u = son[u][c];
  }
  cnt[u]++;
}

Insert(s);

查询

同样的，枚举字符串的每个字符，每次走到对应边上，如果没有直接返回 \(0\)。

单次时间复杂度 \(O(|S|)\)

代码

int Getsum(const string &s) {
  int u = 1;
  for(char c : s) {
    if(!son[u][c]) {
      return 0;
    }
    u = son[u][c];
  }
  return cnt[u];
}

Getsum(s);

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 1001;

struct Trie {
  int tot = 1, cnt[MAXN], son[MAXN][256];
  void Insert(const string &s) {
    int u = 1;
    for(char c : s) {
      if(!son[u][c]) {
        son[u][c] = ++tot;
      }
      cnt[u]++;
      u = son[u][c];
    }
    cnt[u]++;
  }
  int Getsum(const string &s) {
    int u = 1;
    for(char c : s) {
      if(!son[u][c]) {
        return 0;
      }
      u = son[u][c];
    }
    return cnt[u];
  }
}tr;

int n, m;

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1; i <= n; ++i) {
    string s;
    cin >> s;
    tr.Insert(s);
  }
  for(int i = 1; i <= m; ++i) {
    string s;
    cin >> s;
    cout << tr.Getsum(s) << "\n";
  }
  return 0;
}