[AHOI2005] 洗牌
题目描述
为了表彰小联为 Samuel 星球的探险所做出的贡献,小联被邀请参加 Samuel 星球近距离载人探险活动。
由于 Samuel 星球相当遥远,科学家们要在飞船中度过相当长的一段时间,小联提议用扑克牌打发长途旅行中的无聊时间。玩了几局之后,大家觉得单纯玩扑克牌对于像他们这样的高智商人才来说太简单了。有人提出了扑克牌的一种新的玩法。
对于扑克牌的一次洗牌是这样定义的,将一叠 \(N\)(\(N\)为偶数)张扑克牌平均分成上下两叠,取下面一叠的第一张作为新的一叠的第一张,然后取上面一叠的第一张作为新的一叠的第二张,再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。
如果对一叠 \(6\) 张的扑克牌 \({1,2,3,4,5,6}\),进行一次洗牌的过程如下图所示:
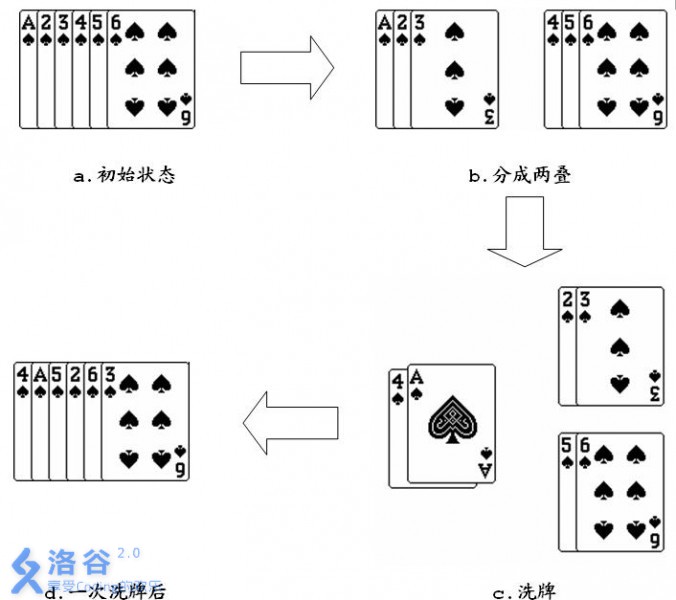
从图中可以看出经过一次洗牌,序列 \(1,2,3,4,5,6\) 变为 \(4,1,5,2,6,3\)。当然,再对得到的序列进行一次洗牌,又会变为 \(2,4,6,1,3,5\)。
游戏是这样的,如果给定长度为 \(N\) 的一叠扑克牌,并且牌面大小从 \(1\) 开始连续增加到 \(N\)(不考虑花色),对这样的一叠扑克牌,进行 \(M\) 次洗牌。最先说出经过洗牌后的扑克牌序列中第 \(L\) 张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利,你能帮助他吗?
输入格式
输入文件中有三个用空格间隔的整数,分别表示 \(N,M,L\)。
(其中 \(1\le N\le 10^{10},0 \le M\le 10^{10}\),且 \(N\) 为偶数)。
输出格式
单行输出指定的扑克牌的牌面大小。
样例 #1
样例输入 #1
6 2 3
样例输出 #1
6
提示
\(0 < N \leq 10^{10}\),\(0 \leq M \leq 10^{10}\),且 \(N\) 为偶数。
分析
由题,易得
每次洗牌后第 \(i\) 张牌会转移到第 \(2*i \%(n+1)\) 的位置上
即在\(mod(n+1)\)意义下,\(i\) 和 \(2i\) 是同余的
即
\[i * 2^{m} \equiv l \qquad(mod (n+1)) \]再稍微导亿导
\[2^{m} * i + (n+1) * k = l \]\[2^{m} * \frac{i}{l} + (n+1) * \frac{k}{l}=1 \]之后利用exgcd求出\(\frac{i}{l}\)解再乘上l就可以了
\(\\\)
\(\\\)
吗?
千辛万苦打出代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 0x3f
#define INF 1e9+100
#define mst(a,b) memset(a,b,sizeof(a))
#define re register
#define Elaina 0
const int N = 10000100;
inline int read(){
int x=0,f=1;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
return x*f;
}
int t,n,m,k,mod,ans;
int s[N],p[N],l[N];
bool vis[N];
int exgcd(int a,int b,int &x,int &y){
if(!b){
x=1;
y=0;
return a;
}
int res=exgcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
return res;
}
int qpow(int a, int b){
int res=1;
while(b){
if(b&1){
res=res*a%(n+1);
}
a=a*a%(n+1);
b>>=1;
}
return res;
}
main(){
n=read(),m=read(),k=read();
int p=qpow(2,m);
int xx,yy;
exgcd(p,n+1,xx,yy);
while(xx<0){
xx+=n+1;
}
return printf("%lld",xx*k%(n+1)),Elaina;
}

WA了
为啥呢
简单推算可知
longlong他爆掉了
那咋办呢
__int128
__int128固然是可以的 但他太低端
有个东西 他叫“龟速乘”
即牺牲时间而保证你的longlong不会boom一下爆掉~
他长这样↓ 和快速幂几乎是别无二致
int mul(int a,int b,int mod){
int res=0;
while(b){
if(b&1){
res=(res+a)%mod;
}
a=(a+a)%mod;
b>>=1;
}
return res%mod;
}
code
Elaina's code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 0x3f
#define INF 1e9+100
#define mst(a,b) memset(a,b,sizeof(a))
#define re register
#define Elaina 0
const int N = 10000100;
inline int read(){
int x=0,f=1;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
return x*f;
}
int t,n,m,k,mod,ans;
//int ;
//bool ;
int exgcd(int a,int b,int &x,int &y){
if(!b){
x=1;
y=0;
return a;
}
int res=exgcd(b,a%b,x,y);
// x^=y^=x^=y;
// y-=a/b*x;
int t=x;
x=y;
y=t-a/b*y;
return res;
}
int mul(int a,int b,int mod){
int res=0;
while(b){
if(b&1){
res=(res+a)%mod;
}
a=(a+a)%mod;
b>>=1;
}
return res%mod;
}
int qpow(int a,int b,int mod){
int res=1;
while(b){
if(b&1){
res=mul(res,a,mod);
}
a=mul(a,a,mod);
b>>=1;
}
return res%mod;
}
main(){
n=read(),m=read(),k=read();
int p=qpow(2,m,n+1);
int xx,yy;
exgcd(p,n+1,xx,yy);
while(xx<0){
xx+=n+1;
}
printf("%lld",mul(xx,k,n+1));
return Elaina;
}
都看到这了,真的不点个赞吗(>ω<*)