P3805 【模板】manacher 算法

题意

给定一个字符串，求所有字串中的最长回文串。

思路

暴力肯定过不了，如果在一个已经求出来的回文串中知道左半边，也肯定知道右半边，那么设 \(d_i\) 为以 \(i\) 为中心的回文串（奇数长度）的最长半径，那么在一个回文串 \([l,r]\) 中，知道 \(d_{l + (r - i)}(l \le i \le r)\)，那么回文串的另一边 \(d_i\) 也可以得出，因为回文串两边相同
，d也会相同。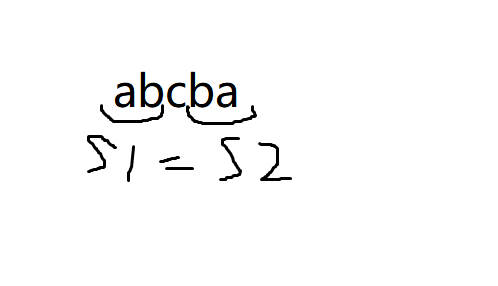
那么对于已经求出来的 \([l, r]\)，如果要求 \(d_i\)，如果 \(i\) 在区间内（不会比 \(l\) 小，因为那是比它小的编号的回文串的左端点 \(l \le j \le i\)），那么就可以用已经求出来的 \(d_{l + (r - i)}\)（\(r - i\) 相当于是它离末尾有几格，以上图为例（下标从1开始） \(i = 4\)， 它离末尾的距离是 \(r - i\), 那么它的对面就是 \(l + (r - i)\)，其实可以把它看作：他对面的离起始有几格）来得到 \(d_i\)，但是 \(d_i\) 其实是可以继续扩展的，所以在往外扩展扩展即可，如果不在区间内（\(i > r\)），那么没有可以用的，只能自力更生，用 \(n^2\) 的方法做。如果是长度为偶数就改一下即可。

代码

#include <iostream>
#include <string>

using namespace std;

const int MaxN = 1.1e7 + 10;

int d[3][MaxN], n, ans;
string s;

void G(int f, int x) {  // 自力更生
  while (x - d[f][x] + f - 1 >= 0 && x + d[f][x] < n && s[x - d[f][x] + f - 1] == s[x + d[f][x]]) {
    d[f][x]++;
  }
  d[f][x]--;
}

int main() {
  ios::sync_with_stdio(0);
  cin.tie(0), cout.tie(0);
  cin >> s, n = s.size();
  for (int i = 0, l = 0, r = -1; i < n; i++) {                         // r 好像必需是-1，为了0除可以自力更生
    d[1][i] = i > r ? 1 : min(d[1][l + (r - i)], r - i + 1), G(1, i);  // 自力更生或是用之前已经算好的
    if (i + d[1][i] > r) {
      r = i + d[1][i], l = i - d[1][i];
    }
    ans = max(ans, d[1][i] * 2 + 1);
  }
  for (int i = 0, l = 0, r = -1; i < n; i++) {
    d[2][i] = i > r ? 1 : min(d[2][l + (r - i - 1)], r - i - 1), G(2, i);
    if (i + d[2][i] > r) {
      r = i + d[2][i], l = i - d[2][i] + 1;
    }
    ans = max(ans, d[2][i] * 2);
  }
  cout << ans << '\n';
  return 0;
}

时间复杂度

最外层的for肯定运行 \(n\) 次，而 \(r\)，肯定是单调不减的，所以也只会最多变 \(n\)，自力更生处因为会用到之前已经算出来的，所以也只会最多运行 \(n\) 次，\(l\) 根本不用管，因为是由着 \(r\) 的，所以总共 \(O(n)\)