[YsOI2020] 植树(洛谷)
题目背景
Ysuperman 响应号召,决定在幼儿园里植树。
题目描述
Ysuperman 有一棵 \(n\) 个节点的无根树 \(T\)。如果你不知道树是什么,TA 很乐意告诉你,树是一个没有环的无向联通图。
既然树是无根的,那就没有办法种植。Ysuperman 研究了很久的园艺,发现一个节点如果可以成为根,它必须十分平衡,这意味着以它为根时,与它直接相连的节点,他们的子树大小都相同。
你作为幼儿园信息组一把手,Ysuperman 给你一棵树,你能在 \(1s\) 内找到所有可能成为根的节点吗?
输入格式
第一行一个正整数 \(n\),表示树的节点个数。
此后 \(n-1\) 行,每行两个正整数 \(u_i,v_i\),表示树上有一条直接连接 \(u_i,v_i\) 的边。保证每条边只会给出一次。
输出格式
不超过 \(n\) 个从小到大的整数,用空格隔开,表示每一个可能成为根的节点。
样例 #1
样例输入 #1
2
1 2
样例输出 #1
1 2
样例 #2
样例输入 #2
4
1 2
2 3
3 4
样例输出 #2
1 4
样例 #3
样例输入 #3
9
1 2
1 3
4 1
5 1
1 6
1 9
8 1
1 7
样例输出 #3
1 2 3 4 5 6 7 8 9
提示
样例说明
样例说明 \(1\)。
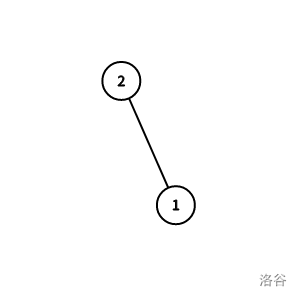
以 \(1\) 为根时,与 \(1\) 直接相连的点有 \(\{2\}\),因为只有一个所以大小全部相同。
以 \(2\) 为根时,与 \(2\) 直接相连的点有 \(\{1\}\),因为只有一个所以大小全部相同。
所以答案为 \(1,2\)。
样例说明 \(2\)
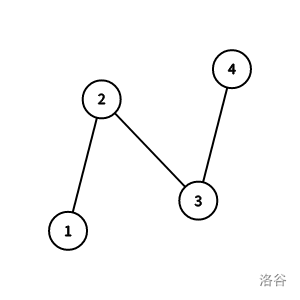
以 \(1\) 为根时,与 \(1\) 直接相连的点有 \(\{2\}\),因为只有一个所以大小全部相同。
以 \(2\) 为根时,与 \(2\) 直接相连的点有 \(\{1,3\}\),子树大小分别为 \(\{1,2\}\),不相同。
以 \(3\) 为根时,与 \(3\) 直接相连的点有 \(\{2,4\}\),子树大小分别为 \(\{2,1\}\),不相同。
以 \(4\) 为根时,与 \(4\) 直接相连的点有 \(\{3\}\),因为只有一个所以大小全部相同。
所以答案为 \(1,4\)。
数据范围
本题采用捆绑测试。
| \(\rm{subtask}\) | \(n\) | 分数 |
|---|---|---|
| \(1\) | \(\le 5000\) | \(40\) |
| \(2\) | \(\le 10^6\) | \(60\) |
对于 \(100\%\) 的数据,满足 \(1 \le n\le 10^6\)。
提示
由于输入输出量较大,你可能需要快速输入/输出。
解答
注意
root数组是判断当前节点是否可以作为根num是计算当前节点子树大小- 最后在
for循环外面加加是当前节点也加1 flag的妙用- 无向图,数组开两倍
#include <iostream>
#include <cstring>
using namespace std;
const int N = 2e6 + 10;
bool st[N];
bool root[N];
int num[N];
int h[N], e[N], ne[N], idx;
int n;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dfs(int u)
{
root[u] = 1;
int flag = 0;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true;
num[u] += dfs(j);
if (!flag) flag = num[j];
if (flag != num[j]) root[u] = 0;
}
}
num[u]++;
// 这个作用就是判断当前节点作为根节点是否满足
// n - num[u]是另一个分支
// flag是一个分支,相当于是构造了二叉树
// 看题解的图
if (u != 1 && flag && flag != n - num[u]) root[u] = 0;
return num[u];
}
int main()
{
cin >> n;
int n1 = n - 1;
memset(h, -1, sizeof h);
while (n1--)
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
st[1] = true;
dfs(1);
for (int i = 1; i <= n; i++)
if (root[i])
printf("%d ", i);
return 0;
}