关路灯

题目描述

某一村庄在一条路线上安装了 \(n\) 盏路灯，每盏灯的功率有大有小（即同一段时间内消耗的电量有多有少）。老张就住在这条路中间某一路灯旁，他有一项工作就是每天早上天亮时一盏一盏地关掉这些路灯。

为了给村里节省电费，老张记录下了每盏路灯的位置和功率，他每次关灯时也都是尽快地去关，但是老张不知道怎样去关灯才能够最节省电。他每天都是在天亮时首先关掉自己所处位置的路灯，然后可以向左也可以向右去关灯。开始他以为先算一下左边路灯的总功率再算一下右边路灯的总功率，然后选择先关掉功率大的一边，再回过头来关掉另一边的路灯，而事实并非如此，因为在关的过程中适当地调头有可能会更省一些。

现在已知老张走的速度为 \(1m/s\)，每个路灯的位置（是一个整数，即距路线起点的距离，单位：\(m\)）、功率（\(W\)），老张关灯所用的时间很短而可以忽略不计。

请你为老张编一程序来安排关灯的顺序，使从老张开始关灯时刻算起所有灯消耗电最少（灯关掉后便不再消耗电了）。

输入格式

第一行是两个数字 \(n\)（表示路灯的总数）和 \(c\)（老张所处位置的路灯号）；

接下来 \(n\) 行，每行两个数据，表示第 \(1\) 盏到第 \(n\) 盏路灯的位置和功率。数据保证路灯位置单调递增。

输出格式

一个数据，即最少的功耗（单位：\(J\)，\(1J=1W\times s\)）。

样例 #1

样例输入 #1

5 3
2 10
3 20
5 20
6 30
8 10

样例输出 #1

270

提示

样例解释

此时关灯顺序为 3 4 2 1 5。

数据范围

\(1\le n\le50\)，\(1\le c\le n\)，\(1\le W_i \le 100\)。

题解

分析

本题是一道经典的区间dp，时间复杂度为 \(O(n^2)\) 。

首先可以发现，老张走的路线上经过的所有灯都会被关闭，因为关灯不会花费任何时间。

同时，老张走过的路线也可以抽象成下面的图。

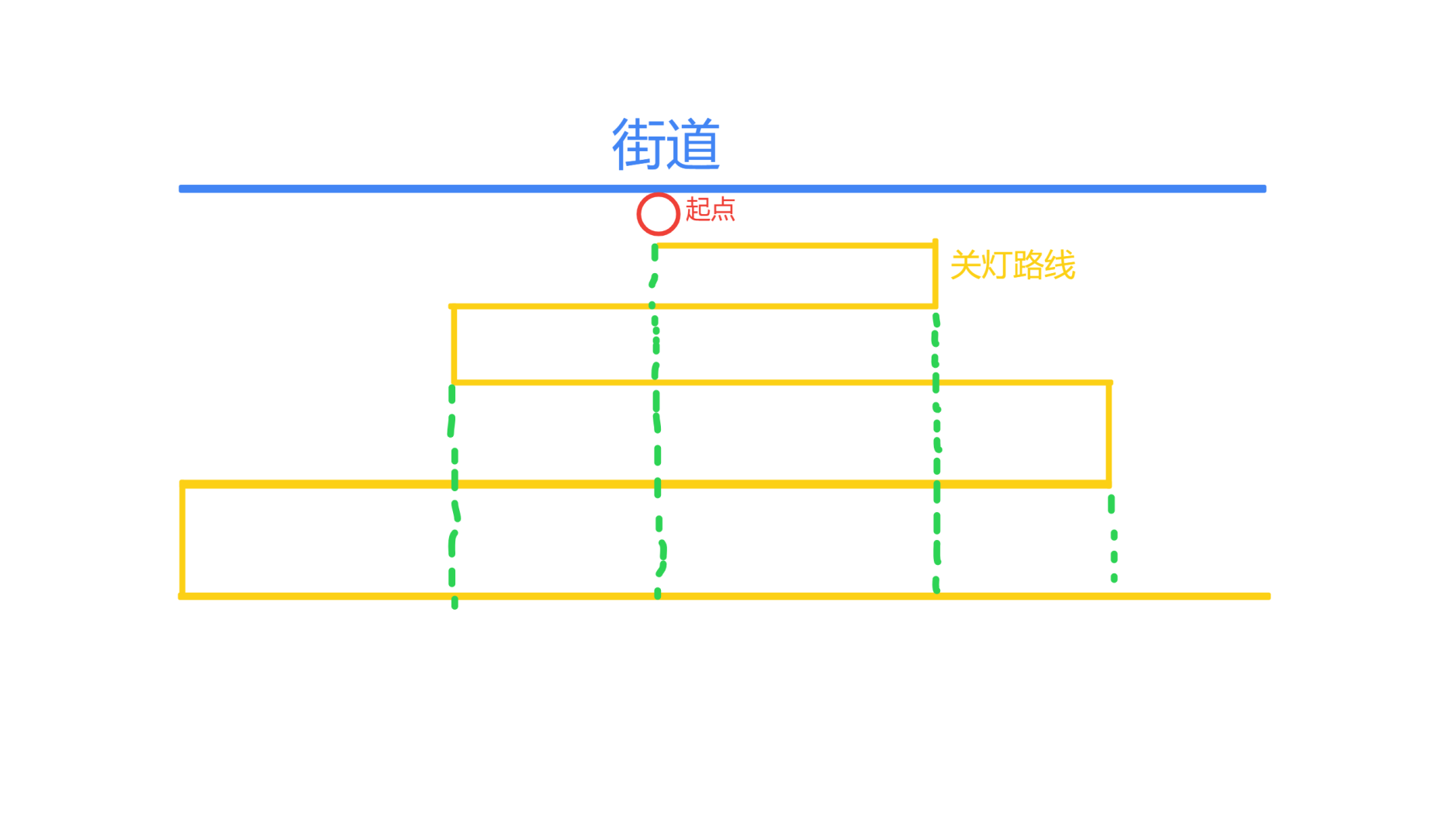
观察可知，每行路线后的下一行路线都比这一行路线要长。

因此，我们可以把街道看成一个区间，\(f_{i,j}\) 表示从横坐标为 \(i\) 的点走到横坐标为 \(j\) 的点耗费的最少电量。

同时由于路线上的所有灯都会被关闭，所以 \(f_{i,j}\) 也表示关闭从横坐标为 \(i\) 的灯到横坐标为 \(j\) 的灯所用的最少电量 。

但是对于一个 \([ i , j ]\) 的区间，老张既可能站在 \(i\) 上，也可能站在 \(j\) 上。

所以还要再加一维 \(f_{i,j,k}\) , 当 \(k=0\) 时表示老张站在 \(i\) 上，当 \(k=1\) 时表示老张站在 \(j\) 上。

并且，对于横坐标为 \(x\) 的一个点而言，它的这一步既可以是从上一步顺着走过来的，也可以是在上一步之后突然转弯走过来的。

因此，在计算 \(f_{i,j,k}\) 的时候，应该进行分类讨论。

\(f_{i,j,k} = \begin{cases} k=0 \begin{cases} \text{ 来自 } i+1 \\ \\ \text{ 来自 } j \\ \end{cases} \\ \\ k=1 \begin{cases} \text{ 来自 } j-1 \\ \\ \text{ 来自 } i \\ \end{cases} \end{cases}\)

\(i+1\) 是 \(i\) 的右边，由于 \(i\) 为区间的左端点，代表 \(i\) 为从左往右数第一个熄灭的灯，所以 \(i\) 的左边不可能有当前被关掉的灯，只有右边 \(i+1\) 有被熄灭的灯，所以从 \(i+1\) 走来 ；而 \(j\) 代表到了右端点 \(j\)，突然不往右边走了，折返回 \(i\) 。

\(j-1\) 是 \(j\) 的左边，由于 \(j\) 为区间的右端点，代表 \(j\) 为从右往左数第一个熄灭的灯，所以 \(j\) 的右边不可能有当前被关掉的灯，只有左边 \(j-1\) 有被熄灭的灯，所以从 \(j-1\) 走来 ；而 \(i\) 代表到了左端点 \(i\)，突然不往左边走了，折返回 \(j\) 。

实现

不难发现，至此问题已经和 合并石子 问题非常相似了。

我们可以把路灯看成一个个石子，然后从老张的起始位置开始合并区间，直到把 \([1,n]\) 的区间全部合并完成。

如上文所言，\(f_{i,j,k}\) 表示在 \([i,j]\) 的电灯全部关闭后，老张站在 \(k\) 时的最少已经消耗的电量。
因此，可以写出动态转移方程式：

\(f_{i,j,0} = min \begin{cases} f_{i+1,j,0} &+ &cal( ) \\ f_{i+1,j,1} &+ &cal( ) \\ \end{cases}\)

\(f_{i,j,1} = min \begin{cases} f_{i,j-1,0} &+ &cal( ) \\ f_{i,j-1,1} &+ &cal( ) \\ \end{cases}\)

这里的 \(cal()\) 指计算走到目标点花费的电量。

同时，也应当注意状态转移的顺序，要保证每一个区间要用到的子区间全部都求完了。

我们可以设 \(f_{s,s,0}=f_{s,s,1}=0\) ，其它的设为无穷大，这里的 \(s\) 指老张起始坐标。

然后先枚举区间的长度，再从左到右枚举左端点位置，根据长度来推出右端点位置，依次更新 \(f_{i,j,k}\) ，时间 \(O(n^2)\) 。

由于只有其子区间先前被更新过的区间才会被更新，所以状态传递就是从点 \(c\) 扩散到两侧。

每个区间要用到的是比自己短 \(1\) 的子区间，如 \([i+1,j]\) 和 \([i,j-1]\) ，在更新 \([i,j]\) 前长度比他们短的子区间全都更新过了。

这是区间dp问题的通常转移顺序。

细节

上文中，有一个 \(cal()\) 函数我们并未实现，因此我们要来实现它。

我们可以为路灯的位置与电灯的功率定义两个前缀和数组，分别为 \(p[N]\) 与 \(w[N]\) 。（因为题目保证路灯位置一定递增，所以不用给位置排序。）

其中，$p_i=p_{i-1}+p_i ， w_i=w_{i-1}+w_i $ 。但因为题目中已经给你了距离的前缀和，所以不用处理 \(p\) 。

对于一个已经全部关掉的灯的区间 \([l,r]\)，当前站在的地方 \(s\) ，要去到的地方 \(e\) ，我们定义函数 \(cal(l,r,s,e)\)。

其中，起点终点距离为 \(p_{max(s,e)} - p_{min(s,e)}\) ，这里的前缀和求值下标不用 \(-1\) 是因为每个点存的是与一个不存在路灯的 \(0\) 的距离。

由于老张速度为 \(1m/s\) ，所以耗费的时间就是 \(p_{max(s,e)} - p_{min(s,e)}\) 。

同时，所有没关的电灯的功率综合为 \(w_n-w_r+w_{l-1}\) ，\(r\) 不用 \(-1\) 是因为它已经被关了，要被减去功率，而 \(l\) 要 \(-1\) 也是因为它没被关，所以不能加入功率中。

所以，\(cal(l,r,s,e) = (p_{max(s,e)} - p_{min(s,e)})*(w_n-w_r+w_{l-1})\) 。

代码

#include <bits/stdc++.h>
using namespace std;
int p[105],w[105],f[105][105][3],n,c;
int cal(int l,int r,int s,int e)//算出一段的代价
{
    return (p[max(s,e)]-p[min(s,e)])*(w[n]-w[r]+w[l-1]);
}
int main()
{
    memset(f,0x3f,sizeof(f));//初始化代价
    cin>>n>>c;
    for(int i=1;i<=n;i++)
    {
        cin>>p[i]>>w[i];
        w[i]+=w[i-1];//只有功率要前缀和，这题的位置题目已经做好前缀和了
    }
    f[c][c][0]=f[c][c][1]=0;//把c设为0，不然无法更新其他点
    for(int l=2;l<=n;l++)//枚举每个区间长度
    {
        for(int np=1;np+l-1<=n;np++)//枚举每个区间的起点
        {
            //由于只有其子区间先前被更新过的区间才会被更新，所以状态传递就是从点c扩散到两侧
            //每个区间要用到的是比自己短1的子区间，如[i+1,j]和[i,j-1]，在更新[i,j]前长度比他们短的子区间全都更新过了
            int i=np,j=np+l-1;//i左端点，j右端点
            f[i][j][0]=min(f[i+1][j][0]+cal(i+1,j,i+1,i),f[i+1][j][1]+cal(i+1,j,j,i));
            f[i][j][1]=min(f[i][j-1][0]+cal(i,j-1,i,j),f[i][j-1][1]+cal(i,j-1,j-1,j));
        }
    }
    cout<<min(f[1][n][0],f[1][n][1]);//输出结尾为左右端点中较小代价的那一个
    return 0;
}