[ABC217F] Make Pair 题解

思路解析

通过 \(n \le 200\) 和 “选出的两个学生离开队列，空出来的位置左右合拢” 这两个细节可以想到能用区间 dp 做，\(f_{i,j}\) 表示将 \(i \to j\) 这个区间全部选完的方案数，然后常规区间 dp，加一个判断如果当前区间 \([l,r]\) 中 \(l,r\) 是朋友，就可以从 \([l+1,r-1]\) 推过来，于是加上 \(f_{l+1,r-1}\) 代表除去两个端点后的区间方案数。

接下来是重点，就是遍历每一个 \(k\)，然后统计 \(f_{l,k}+f_{k+1,r}\)，表示枚举每一个中间点，统计从该点切割开来的两半的贡献。如果对于这一点不太理解，建议去做 P1063 [NOIP2006 提高组] 能量项链 学习区间 dp。但是题目要求方案数，就很有可能出现判重，例如：

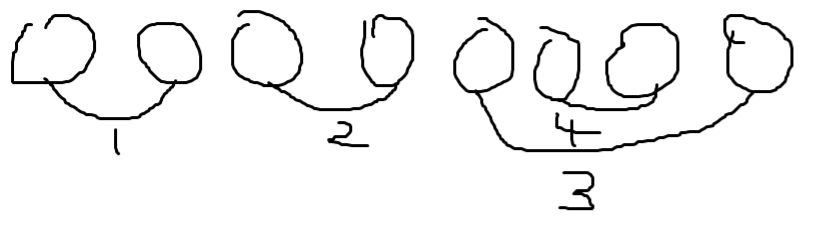
这体现了一个区间 \([l,r]\) 的学生示意图，圆圈代表学生，连线代表他们是朋友关系，线上的数字用于区分标记。接下来有几种可能的 \(k\) 的取值。

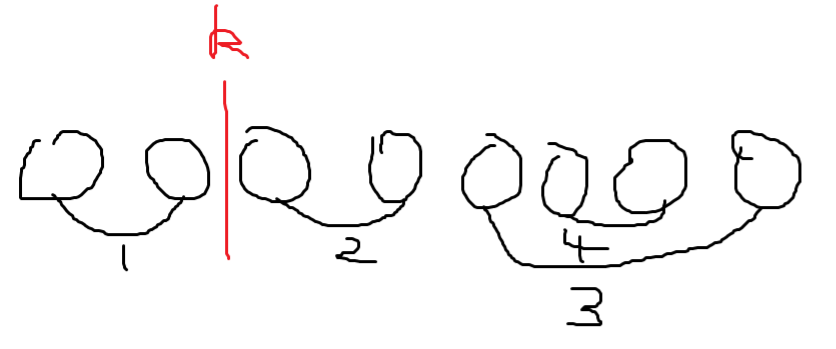
这种情况下可能出现的方案有：【1，2，3，4】，【2，1，3，4】，【1，3，4，2】……

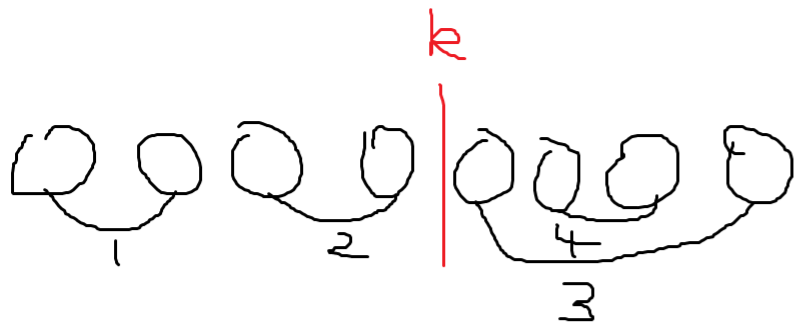
这种情况下的方案则和上一种情况一模一样，原因则是因为我们没有给 \(k\) 的可能性做一个判断。可以想到我们的 \(k\) 的取值一定会与端点有联系，于是在转移前判断 \(k\) 是否与 \(l\) 连接，这样就可以有效排除掉重复的方案，因为我们需要统计的根本是和 \(l\) 联系的那一部分（例如我的例子中的 1 号朋友）加上和 \(l\) 没联系的部分（例如我的例子中的2，3，4），这样就可以排除掉 \(k\) 与当前 \(l\) 无关的重复方案。

最后就是由于是算方案数，就说明区间 \([l,k]\) 和 \([k+1,r]\) 中每一种可能的方案在两段合并到一起后当前方案中的元素出现的相对顺序不会改变，例如：

左边的 1，2，3 代表区间 \([l,k]\) 中的一种可行方案，右边的 a，b 代表区间 \([k+1,r]\) 中的一种可行方案，那么当两者合并后的可行方案的顺序就有可能是：

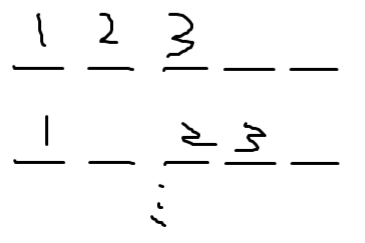
这里不放出 a，b 是因为合并后原来一个方案中的相对顺序不会改变，画出横线是为了更好理解其实这就是一个在横线中填入相对顺序有序数字的一个问题，其实这个例子的方案数就是 \(\mathrm{C}_5^3\)，扩展到所有方案就是 \(\mathrm{C}_{len/2}^{(k-l+1)/2}\)。于是便在状态转移时乘上该式即可。

时间复杂度：三层区间 dp，每层最大都是 \(n\)，复杂度 \(O(n^3)\)。

code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1010;
const ll mod = 998244353;
ll n, m, f[N][N], c[N][N];
bool frd[N][N];
int main() {
	cin >> n >> m;
	n *= 2ll;
	for(int i = 1, a, b; i <= m; i++) {
		cin >> a >> b;
		frd[a][b] = frd[b][a] = true;	//标记为朋友
	}
	for(int i = 1; i <= n; i++) f[i + 1][i] = 1;
	c[0][0] = 1;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= i; j++) {
			c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;	//预处理组合数
		}
	}
	for(int i = 2; i <= n; i += 2) {
		for(int l = 1, r = l + i - 1; l + i - 1 <= n; l++, r++) {
			if(frd[l][r]) f[l][r] = f[l + 1][r - 1];	//小特判
			for(int k = l + 1; k <= r - 1; k += 2) {
				int l1 = (k - l + 1) / 2, l2 = (r - k) / 2;
				if(frd[l][k]) {	//去重的关键
					f[l][r] = (f[l][r] + ((f[l + 1][k - 1] * f[k + 1][r]) % mod * c[i / 2 + 1][l1 + 1]) % mod) % mod;	//注意要乘上组合数
				}
			}
		}
	}
	cout << f[1][n];
	return 0;
}