首页 > 其他分享 >Codeforces-Pinely-Round-3

Codeforces-Pinely-Round-3

时间：2024-02-08 10:11:48浏览次数：24  
标签：return int Pinely Codeforces long while inline Round MOD

比赛链接

A. Distinct Buttons

扣掉一个方向就是只能走到相邻两个象限以及和这两个象限相邻的坐标轴上，判一下是不是所有的点都满足就行。

判的时候只需要判是否所有 \(x \le 0\)(落到二、三象限)，或者所有 \(x \ge 0\)(四、一象限)，或者所有 \(y \le 0\) 或者所有 \(y \ge 0\) 就行，时间复杂度 \(\mathcal{O}(n)\)。

code for A 
#include <bits/stdc++.h>

using namespace std;

inline void solve() {
    int n; cin >> n;
    bool xge0 = true, xle0 = true;
    bool yge0 = true, yle0 = true;
    while(n --) {
        int x, y; cin >> x >> y;
        if(x < 0) xge0 = false;
        if(x > 0) xle0 = false;
        if(y < 0) yge0 = false;
        if(y > 0) yle0 = false;
    }
    if(xge0 || xle0 || yge0 || yle0)
        cout << "YES" << '\n';
    else
        cout << "NO" << '\n';
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0);

    int T; cin >> T;
    while(T --) solve();

    return 0;
}

B. Make Almost Equal With Mod

显然如果有奇数也有偶数的话直接模 \(2\) 就行，启发我们在二进制上考虑。

写出来所有数的二进制，从低位到高位看是不是所有数的这一位都相同，找到一个同时有 \(0\) 和 \(1\) 的二进制位 \(k\) 后用 \(2^{k+1}\) 模就行，意义是把后 \(k+1\) 位取出来，正好有两种数，时间复杂度 \(\mathcal{O}(n \log w)\)。

code for B 
#include <bits/stdc++.h>

using namespace std;

const int N = 110;
int n; long long A[N];

inline bool check(int bit) {
    long long P = 1ll << (bit + 1);
    for(int i = 2; i <= n; i ++)
        if(A[i] % P != A[i - 1] % P) return true;
    return false;
}

inline void solve() {
    cin >> n;
    for(int i = 1; i <= n; i ++)
        cin >> A[i];

    for(int bit = 0; bit <= 64; bit ++) {
        if(check(bit)) {
            cout << (1ll << bit + 1) << '\n';
            return;
        }
    }
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0);

    int T; cin >> T;
    while(T --) solve();

    return 0;
}

C. Heavy Intervals

一眼题，首先考虑如果区间固定但是 \(c_i\) 不固定答案是多少，显然这时候应该长度小的区间配值大的 \(c_i\)。

然后考虑区间不固定，如果有两个区间 \([l_1,r_1],[l_2,r_2]\) 是交叉不包含的关系，即 \(l_1 < l_2 < r_1 < r_2\)，那么将这两个区间变成包含关系一定更优，即变成 \([l_1,r_2]\) 和 \([l_2,r_1]\)，因为这时候更大的那个 \(c_i\) 的 \(r-l\) 变小了，两个 \(r-l\) 和是固定的，即 \(r_1+r_2-l_1-l_2\)，小的那个 \(c_i\) 的 \(r-l\) 虽然增加了，但是增加的一定不会比减少的多。

所以把所有 \(l,r\) 塞到一起从左到右扫，每遇到一个右端点就把它前面还没有被用过的最靠右的左端点弹出来配对，得到所有区间之后按照长度配 \(c\) 即可，时间复杂度 \(\mathcal{O}(n \log n)\)。

code for C 
#include <bits/stdc++.h>

using namespace std;
typedef pair<int, int> pii;

const int N = 1e5 + 10;
int n, C[N];
vector<pii> vec;
vector<int> len;

inline void solve() {
    cin >> n; vec.clear(), len.clear();
    for(int i = 1; i <= n; i ++) {
        int l; cin >> l;
        vec.push_back({l, -1});
    }
    for(int i = 1; i <= n; i ++) {
        int r; cin >> r;
        vec.push_back({r, 1});
    }
    for(int i = 0; i < n; i ++) cin >> C[i];
    sort(C, C + n, greater<int>());
    sort(vec.begin(), vec.end());
    priority_queue<int> Q;
    for(auto pr : vec) {
        if(pr.second == -1) Q.push(pr.first);
        else {
            int u = Q.top(); Q.pop();
            len.push_back(pr.first - u);
        }
    }
    assert(Q.empty());
    long long ans = 0; sort(len.begin(), len.end());
    for(int i = 0; i < n; i ++)
        ans += 1ll * len[i] * C[i];
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0);

    int T; cin >> T;
    while(T --) solve();

    return 0;
}

D. Split Plus K

先看 \(k=0\) 的时候怎么做，显然我们是把每个数都拆成若干个相同的数，每个原数拆成的数还一样。

若将 \(a\) 拆成 \(y\)，显然必须满足 \(y \mid a\)，此时需要拆 \(\frac{a}{y}-1\) 次，于是 \(y\) 越大越好。

每个 \(a_i\) 拆成的 \(y\) 还要一样，所以 \(y\) 应该是所有 \(a_i\) 的公因数，还要最大的话就是 \(y=\gcd a_i\) 了，此时答案可以直接算，即

\[\sum_{i=1}^{n} \frac{a_i}{y}-1\nonumber \]

当 \(k \ne 0\) 的时候，想法是类似的，将 \(a\) 拆成 \(p\) 个 \(y\)，应该满足 \(a+pk=(p+1)y\)，整理得到 \(p=\frac{a-y}{y-k}=\frac{a-k}{y-k}-1\)。于是 \(y-k\) 应该是 \(a-k\) 的因数，\(y-k\) 要尽可能大的话，就是 \(\gcd(a_i-k)\) 了。

把 \(\gcd(a_i-k)\) 求出来，设为 \(d\)，那么答案就是

\[\sum_{i=1}^{n}\frac{a_i-k}{d}-1\nonumber \]

可以发现这些推导是完全兼容 \(k=0\) 的情况的。

还有无解的情况存在，如果存在数 \(\ge k\) 并且存在数 \(<k\)，一定无解，因为前者拆出来的数一定有至少一个 \(\ge k\)，后者拆出来的数一定有一个至少 \(<k\)，它们不可能相等;同理，若存在数 \(\le k\) 并且存在数 \(>k\)，也一定无解，

总时间复杂度 \(\mathcal{O}(n \log n)\)。

code for D 
#include <bits/stdc++.h>

using namespace std;

const int N = 2e5 + 10;
int n; long long k, A[N];

inline void solve() {
    cin >> n >> k;
    for(int i = 1; i <= n; i ++) cin >> A[i];
{
    bool flag = true;
    for(int i = 2; i <= n; i ++)
        if(A[i] != A[i - 1]) flag = false;
    if(flag) {cout << "0" << '\n'; return; }
}
{
    int cnt = 0;
    for(int i = 1; i <= n; i ++)
        if(A[i] <= k) cnt ++;
    if(cnt != 0 && cnt != n) {cout << "-1" << '\n'; return; }
    cnt = 0;
    for(int i = 1; i <= n; i ++)
        if(A[i] >= k) cnt ++;
    if(cnt != 0 && cnt != n) {cout << "-1" << '\n'; return; }
}
    long long d = 0;
    for(int i = 1; i <= n; i ++)
        d = __gcd(d, A[i] - k);
    long long ans = 0;
    for(int i = 1; i <= n; i ++)
        ans += (A[i] - k) / d - 1;
    cout << ans << '\n';
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0);

    int T; cin >> T;
    while(T --) solve();

    return 0;
}

E. Multiple Lamps

丁真题，考虑一个暴力的想法是把所有灯全点一遍，最后会有 \(\lfloor \sqrt{n} \rfloor\) 栈灯是亮着的(每个灯会被它的每个因数切换一次状态，而非完全平方数的因数个数都是成对出现的)，因此假如 \(\lfloor \sqrt{n} \rfloor \le \lfloor \frac{n}{5} \rfloor\) ，即 \(n \ge 20\) 的时候就可以这么乱搞。

现在 \(n\) 最大只有 \(19\), \(\lfloor \frac{n}{5} \rfloor \le 3\)，随便乱搞。

具体的，我们在处理询问之前预处理出来每个 \(n \le 19\)，有多少点灯的方案是可以使最后亮着的灯数量 \(\le \lfloor \frac{n}{5} \rfloor\) 的，询问时若 \(n \le 19\) 就直接扫一遍这个表，每次 \(\mathcal{O}(m)\) 判断一下是否合法，算一下复杂度是可以过的。

code for E 
#include <bits/stdc++.h>

using namespace std;

const int N = 2e5 + 10;
int n, m, u[N], v[N];

vector<int> mask[20];

inline void solve() {
    cin >> n >> m;
    for(int i = 1; i <= m; i ++)
        cin >> u[i] >> v[i], u[i] --, v[i] --;
    if(n >= 20) {
        cout << n << '\n';
        for(int i = 1; i <= n; i ++)
            cout << i << " \n"[i == n];
        return;
    }
    for(auto x : mask[n]) {
        bool flag = true;
        for(int i = 1; i <= m; i ++)
            if((x >> u[i] & 1) && !(x >> v[i] & 1)) {
                flag = false;
                break;
            }
        if(flag) {
            cout << __builtin_popcount(x) << '\n';
            for(int i = 0; i < n; i ++)
                if(x >> i & 1) cout << i + 1 << ' ';
            cout << '\n';
            return;
        }
    }
    cout << "-1" << '\n';
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0);

    for(int n = 1; n < 20; n ++) {
        auto check = [&](int mask) {
            int state = 0;
            for(int i = 0; i < n; i ++) if(mask >> i & 1) {
                for(int j = i + 1; j <= n; j += i + 1)
                    state ^= 1 << j - 1;
            }
            return __builtin_popcount(state) <= n / 5;
        };
        for(int st = 1; st < (1 << n); st ++)
            if(check(st)) mask[n].emplace_back(st);
    }

    int T; cin >> T;
    while(T --) solve();

    return 0;
}

F1. Small Permutation Problem (Easy Version)

把 \((i,p_i)\) 画在坐标系上，从 \(1\) 到 \(n\) 枚举 \(i\)，\(a_i\) 的限制等价于 \((1..i,1..i)\) 这个矩形中的点数恰为 \(a_i\)，每次考虑新限制比旧限制多的一部分(是一个L形)，若 \(a_i-a_{i-1}=0\)，说明这个L形里没有点，什么都不用做；若 \(a_i-a_{i-1}=1\)，说明这个L形里有一个点，考虑它是在拐点还是边上分开转移：若在拐点上就只有一种方案，否则方案数应该乘 \(2 \times (i-1-a_{i-1})\)；若 \(a_i-a{i-1}=2\)，那么L形中的两个点都不在拐点上，方案数乘 \((i-1-a_{i-1})^2\) 即可，否则若 \(a_i-a_{i-1}<0\) 或 \(a_i-a_{i-1}>2\)，无解。

时间复杂度是 \(\mathcal{O}(n)\)。

code for F1 
#include <bits/stdc++.h>

using namespace std;

const int N = 2e5 + 10, MOD = 998244353;
inline int Plus(int a, int b) {return a + b >= MOD ? a + b - MOD : a + b; }
inline int Minus(int a, int b) {return a - b < 0 ? a - b + MOD : a - b; }
int n, A[N];

inline int solve() {
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> A[i];

    for(int i = 1; i <= n; i ++) if(A[i] > i) return 0;
    for(int i = 2; i <= n; i ++) if(A[i] < A[i - 1] || A[i] - A[i - 1] > 2) return 0;
    if(A[n] != n) return 0;

    int res = 1;
    for(int i = 1; i <= n; i ++) {
        int delta = A[i] - A[i - 1];
        if(delta == 0) continue;
        if(delta == 1) res = Plus(res, 1ll * res * (i - 1 - A[i - 1]) % MOD * 2 % MOD);
        else res = 1ll * res * (i - 1 - A[i - 1]) % MOD * (i - 1 - A[i - 1]) % MOD;
    }
    return res;
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0);

    int T; cin >> T;
    while(T --) cout << solve() << '\n';

    return 0;
}

F2. Small Permutation Problem (Hard Version)

本质是是一样的，就是L形变宽了而已(枚举的时候跳过去 \(a_i=-1\) 的位置，考虑相邻两个有值的 \(a_i\) 之间的L形),中间加一层枚举就行(把L拆成两个矩形，枚举其中一个矩形中点的个数)，这个枚举是均摊 \(\mathcal{O}(1)\) 的。预处理一下阶乘和组合数就可以做到线性复杂度。

code for F2 
#include <bits/stdc++.h>

using namespace std;

const int N = 2e5 + 10, MOD = 998244353;
inline int Plus(int a, int b) {return a + b >= MOD ? a + b - MOD : a + b; }
inline int Minus(int a, int b) {return a - b < 0 ? a - b + MOD : a - b; }
inline int ksm(long long a, int b) {
    long long r = 1;
    while(b) {
        if(b & 1) r = r * a % MOD;
        b >>= 1, a = a * a % MOD;
    }
    return r;
}
int n, A[N], fac[N], inv[N];
inline int C(int a, int b) {return a >= b ? 1ll * fac[a] * inv[b] % MOD * inv[a - b] % MOD : 0; }

inline int solve() {
    cin >> n;
    for(int i = 1; i <= n; i ++) cin >> A[i];

    for(int i = 1; i <= n; i ++) if(A[i] > i) return 0;
    if(A[n] != n && A[n] != -1) return 0;
    A[n] = n;

    int res = 1, lst = 0;
    for(int i = 1; i <= n; i ++) if(A[i] != -1) {
        if(A[lst] > A[i]) return 0;
        int delta = A[i] - A[lst]; if(delta == 0) {lst = i; continue;}
        int ans = 0;
        for(int k = 0; k <= min(lst - A[lst], i - lst) && k <= delta; k ++)
            ans = Plus(ans, 1ll * res * C(lst - A[lst], k) % MOD * C(i - lst, k) % MOD * fac[k] % MOD * C(i - k - A[lst], delta - k) % MOD * C(i - lst, delta - k) % MOD * fac[delta - k] % MOD);
        res = ans, lst = i;
    }
    return res;
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0);

    fac[0] = 1;
    for(int i = 1; i < N; i ++) fac[i] = 1ll * fac[i - 1] * i % MOD;
    inv[N - 1] = ksm(fac[N - 1], MOD - 2);
    for(int i = N - 1; i >= 1; i --) inv[i - 1] = 1ll * inv[i] * i % MOD;

    int T; cin >> T;
    while(T --) cout << solve() << '\n';

    return 0;
}

G. Pumping Lemma

小清新串串题。考虑 \(x+y\) 必然是 \(S,T\) 的一个公共前缀而 \(z\) 必然是 \(S,T\) 的一个公共后缀，因此先求出 \(S,T\) 的LCP(设长度为 \(p\))和LCS(设长度为 \(q\))，那么若 \(p+q<n\)，一定无解。

删掉 \(S\) 的非 \(T\) 后缀部分，同时在 \(T\) 中删去对应长度的前缀，不影响答案：这是因为 \(S\) 的非 \(T\) 后缀部分必然在 \(x\) 中。

用 \((a,b)\) 表示将 \(S\) 分割为 \((S[1,a],S[a+1,b],S[b+1,n])\) 三部分，换句话说，划分方案 \((a,b)\) 就是取 \(x=S[1,a],y=S[a+1,b],z=S[b+1,n]\)。

假设 \((a,b)\) 是一个合法的方案，那么 \((a+1,b+1)\) 也合法当且仅当 \(S_{b+1}=T_{b+1}\)，证明如下：

假如 \(S_{b+1} \ne T_{b+1}\)，显然不合法。否则如下图所示：

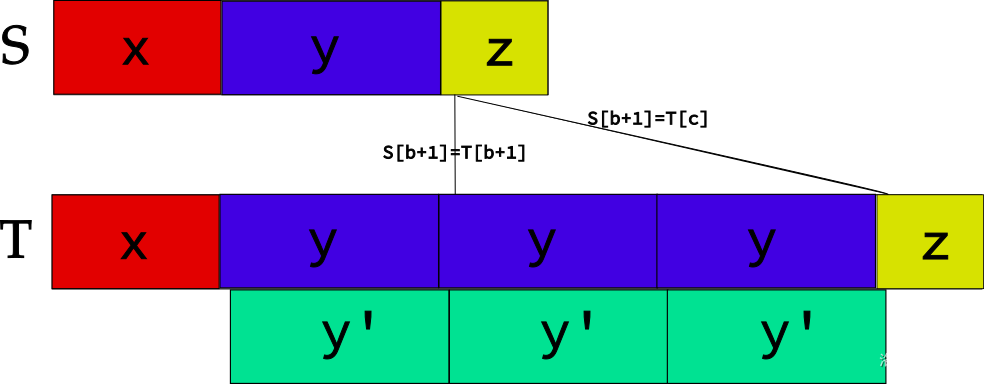
注意到 \(z\) 的第一个字符和 \(y\) 的第一个字符相同，所以等价于将循环节循环移动了一位。

根据上述引理，对于每个 \(|y|\)，若 \((a,b)\) 是该长度(\(|y|=b-a\))的第一个合法分割，那么 \((a+i,b+i),i \ge 0\) 会一直合法，直到一个整数 \(k\) 满足 \(S_{b+k} \ne T_{b+k}\)，在这之后 \((a+i,b+i),i \ge k\) 均会不合法。

接着我们尝试枚举每个 \(|y|=l\)，找到该第一个合法分割 \((a,b)\) 满足 \(b-a=l\)：考虑 \(T\) 的后缀 \(T[l+1,n]\) 和 \(T\) 的LCP，设为 \(c\)，那么 \(T[1,c+l]\) 就是一个具有周期 \(l\) 的串，\(x+y^k\) 必然是其前缀。 \(x\) 只需要满足 \(|x|+|y^k| \le c + |y|\)，而 \(|y^k|=|y|+(m-n)\)，因此合法的 \(x\) 只需要满足 \(|x| \le c-m+n\)，容易计算。

用Z函数预处理 \(T\) 的每个后缀与 \(T\) 的LCP，时间复杂度 \(\mathcal{O}(n)\)。

code for G 
#include <bits/stdc++.h>

using namespace std;

const int N = 1e7 + 10;
int n, m, Z[N]; char S[N], T[N];

int main() {
    ios::sync_with_stdio(false), cin.tie(0);

    cin >> n >> m >> (S + 1) >> (T + 1);
    int c = 0, d = 0;
    while(d < n && S[n - d] == T[m - d]) d ++;
    while(c < n && S[c + 1] == T[c + 1]) c ++;
    if(c + d < n) {
        cout << "0" << '\n';
        return 0;
    }
    int delt = n - d;
    for(int i = delt + 1; i <= n; i ++) S[i - delt] = S[i];
    for(int i = delt + 1; i <= m; i ++) T[i - delt] = T[i];
    n -= delt, m -= delt;
    for(int i = 2, l = 0, r = 0; i <= m; i ++) {
        Z[i] = (i > r ? 0 : min(r - i + 1, Z[i - l + 1]));
        while(i + Z[i] <= m && T[Z[i] + 1] == T[Z[i] + i])
            Z[i] ++;
        if(Z[i] + i - 1 > r) l = i, r = i + Z[i] - 1;
    }

    long long ans = 0;
    for(int i = 1; i <= m; i ++) if((m - n) % i == 0) {
        int len = i + m - n, r = i + Z[i + 1];
        ans += max(r - len + 1, 0);
    }
    cout << ans << '\n';

    return 0;
}

标签：return,int,Pinely,Codeforces,long,while,inline,Round,MOD
From： https://www.cnblogs.com/313la/p/18010418

相关文章

  • Codeforces Round 923 (Div. 3)
    CodeforcesRound923(Div.3)A-MakeitWhite分析在字符串中找到第一个B的位置l和最后一个B的位置r,打印r-l+1即可如果找不到B打印-1code#include<bits/stdc++.h>#defineintlonglong#defineyescout<<"YES"<<'\n'#defineno cout<<"NO"......
  • Codeforces Round 921 (Div. 2)
    https://codeforces.com/contest/1925恶心round，从C题开始每题都是一眼看出做法但是细节挺多的题，烦的一比。A.WeGotEverythingCovered!*800给定\(n,k\)，若所有长度为\(n\)且仅由字母表中前\(k\)个小写字母组成的串都是\(s\)的子序列，则称\(s\)是"EverythingCover......
  • Codeforces Round 923 (Div. 3)(A~F)
    目录ABCDEFA#include<bits/stdc++.h>#defineintlonglong#definerep(i,a,b)for(inti=(a);i<=(b);++i)#definefep(i,a,b)for(inti=(a);i>=(b);--i)#definepiipair<int,int>#definepllpair<longlong,longlong>#de......
  • Codeforces-Hello-2024-Round
    比赛链接A.WalletExchange签到，某个人操作的时候只要一方有金币就行，所以最终赢的应该是拿到最后一个硬币的人，当\(a+b\equiv1\pmod2\)的时候Alice获胜，否则Bob获胜。时间复杂度\(\mathcal{O}(1)\)。codeforA#include<bits/stdc++.h>usingnamespacestd;inli......
  • P10125 「Daily OI Round 3」Simple题解
    原题传送门题目概述：给我们一个字符串，不区分大小写，让我们判断此字符串是与Acoipp等价，还是与Svpoll等价，或者是与前两者都不等价，并按题目条件输出。思路分析：我们只需要把此字符串的第一个字符转成大写，其他字符转成小写，并与那两个字符串进行比较就行了代码：#include<bits/st......
  • 无涯教程-Math.round(x)函数
    将数字四舍五入到最接近的整数。Math.round(x)-语法Math.round(x);x  - 代表数字Math.round(x)-示例console.log("---Math.round()---")console.log("Math.round(7.2):"+Math.round(7.2))console.log("Math.round(-7.7):"+Math.round(-7.......
  • Codeforces Round 920 (Div. 3)（A~F）
    目录ABCDEFA按题意模拟即可#include<bits/stdc++.h>#defineintlonglong#definerep(i,a,b)for(inti=(a);i<=(b);++i)#definefep(i,a,b)for(inti=(a);i>=(b);--i)#definepiipair<int,int>#definepllpair<longlong,longlong......
  • Codeforces div2 C题补题
    Codeforcesdiv2C题补题1922C.ClosestCitiesC.ClosestCities很容易看出，端点的两个城市的最近城市就是他的直接后继和直接前驱，而中间的城市的最近城市就是他前驱和后继中距离绝对值最小的那个，因此我们可以先预处理出每个城市对应的最近城市，用map存储。然后因为区间可以从......
  • Codeforces Round 913 (Div. 3) G.
    题目链接G.把灯看成节点，灯之间的关系看成有向边得到基环树森林若节点的入度为0，那么它一定要用一次开关，这是可以确定的所以用拓扑，把这些确定贡献的节点删去然后就剩下了若干个环若环上有奇数个权值为1的节点，那么不可能全部关上对于环上一个打开的灯，它要么直接用自己的开关......
  • Codeforces Round 921 (Div. 1) 题解
    HelloAd-HocForces！A字符集为前\(k\)个小写字母，给定长度为\(m\)的字符串，求所有的长度为\(n\)的字符串是否是这个字符串的子串。（此处字串不连续）如果不是需要给出反例。\(1\len,k\le26\)，\(1\lem\le1000\)。\(\sumn,\summ\le10^6\)sol.D1A就是神秘贪心，汗流浃背......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99